Mediatriz

Rosimar Gouveia

Professora de Matemática e Física

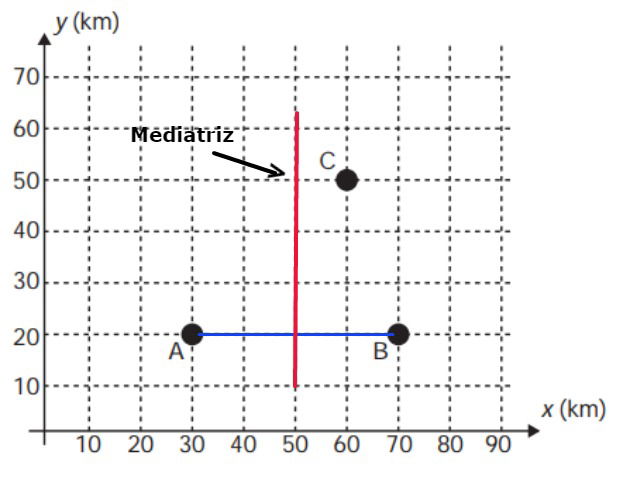
Mediatriz é uma reta perpendicular a um segmento de reta e que passa pelo ponto médio deste segmento.

Todos os pontos pertencentes a mediatriz são equidistantes das extremidades deste segmento.

Lembrando que, diferente da reta, que é infinita, o segmento de reta é limitado por dois pontos de uma reta. Ou seja, ele é considerado uma parte da reta.

Diferença entre reta e segmento de reta

Como construir a mediatriz?

Podemos construir a mediatriz de um segmento de reta $pilha A B com barra acima$ usando régua e compasso. Para isso, siga os seguintes passos:

Desenhe um segmento de reta e nas suas extremidades marque o ponto A e o ponto B.
Pegue um compasso e faça uma abertura que seja um pouco maior que a metade da medida do segmento.
Com essa abertura, coloque a ponta seca do compasso no ponto A e trace um semicírculo. Permanecendo com a mesma abertura no compasso, faça a mesma coisa no ponto B.
Os semicírculos traçados se cruzaram em dois pontos, um acima do segmento de reta e outro abaixo. Com a régua, una esses dois pontos, essa reta traçada é a mediatriz do segmento AB.

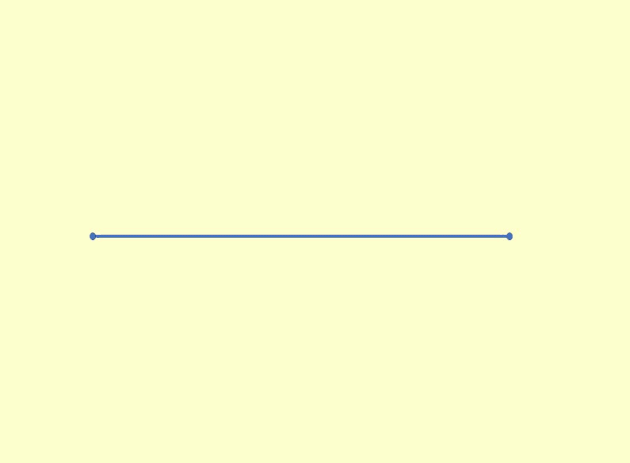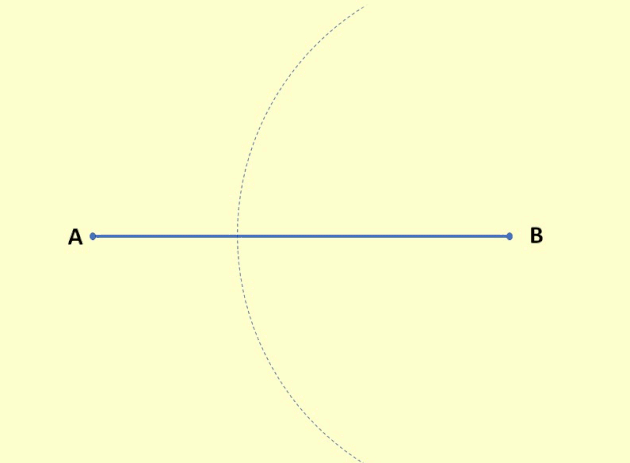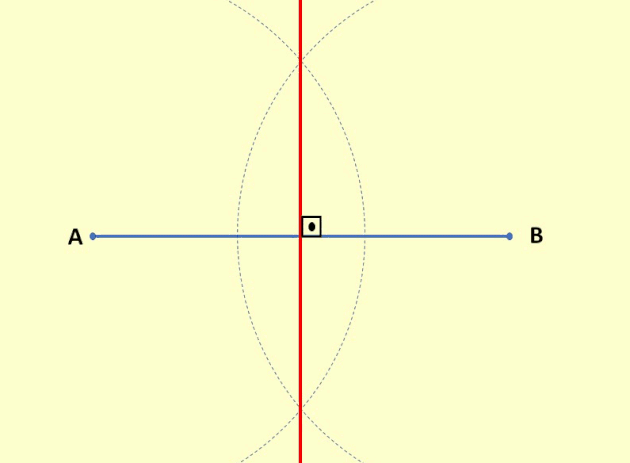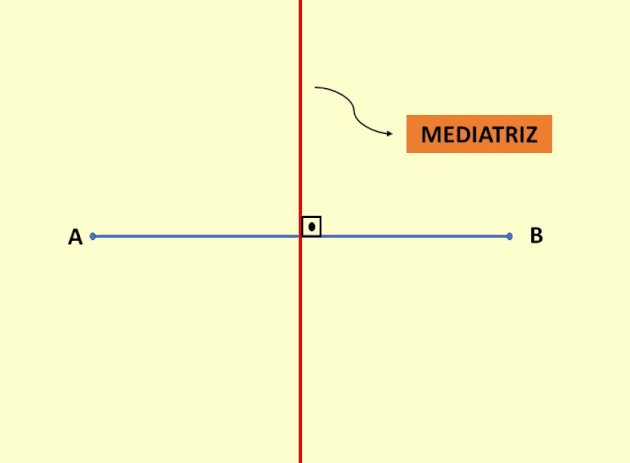
Mediatriz de um triângulo

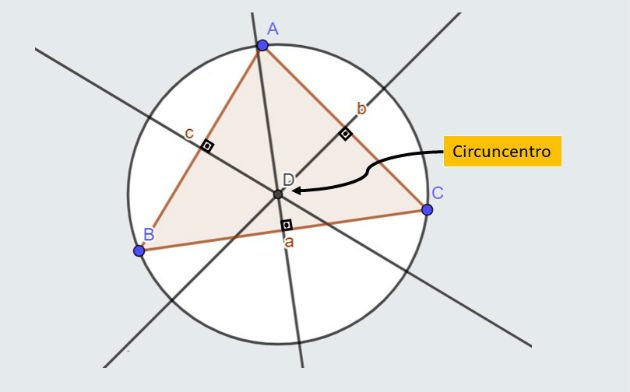
As mediatrizes de um triângulo são retas perpendiculares traçadas passando pelo ponto médio de cada um dos seus lados. Desta forma, um triângulo possui 3 mediatrizes.

O ponto de encontro dessas três mediatrizes é chamado de circuncentro. Este ponto, que está a uma mesma distância de cada um dos seus vértices, é o centro da circunferência circunscrita no triângulo.

Mediana, bissetriz e altura de um triângulo

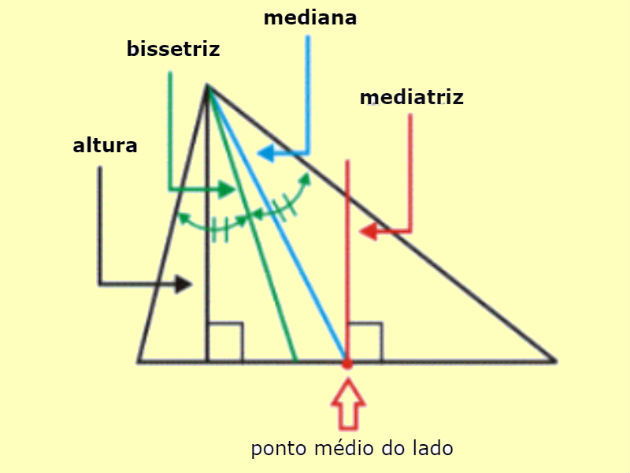
Em um triângulo, além das mediatrizes, podemos construir medianas, que são segmentos de retas que também passam pelo ponto médio dos lados.

A diferença é que enquanto a mediatriz forma um ângulo de 90º com o lado, a mediana une o vértice ao ponto médio dos lados opostos formando um ângulo que pode ou não ser de 90º.

Podemos ainda traçar alturas e bissetrizes. A altura também é perpendicular aos lados do triângulo, mas que parte do seu vértice. Diferente da mediatriz, a altura não passa necessariamente pelo ponto médio do lado.

Partindo do vértice, podemos traçar as bissetrizes internas, que são segmentos de retas que dividem os ângulos do triângulo em dois outros ângulos de mesma medida.

Em um triângulo, podemos traçar três medianas e elas se encontram em um ponto chamado baricentro. Este ponto é denominado o centro de gravidade de um triângulo.

O baricentro divide as medianas em duas partes, visto que a distância do ponto ao vértice é o dobro da distância do ponto ao lado.

Enquanto o ponto de encontro das alturas (ou de seus prolongamentos) é chamado de ortocentro, o encontro das bissetrizes internas é chamado de incentro.

Exercícios resolvidos

1) Epcar - 2016

Um terreno com formato de um triângulo retângulo será dividido em dois lotes por uma cerca feita na mediatriz da hipotenusa, conforme mostra figura.

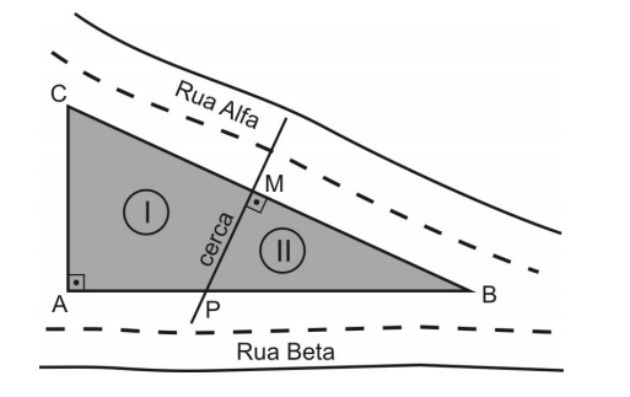
Sabe-se que os lados AB e BC desse terreno medem, respectivamente, 80 m e 100 m. Assim, a razão entre o perímetro do lote I e o perímetro do lote II, nessa ordem, é

$a parêntese direito espaço 5 sobre 3 b parêntese direito 10 sobre 11 c parêntese direito 3 sobre 5 d parêntese direito 11 sobre 10$

Ver Resposta

Para encontrar a razão entre os perímetros, é necessário conhecer a medida de todos os lados do lote I e do lote II.

Entretanto, não conhecemos as medidas dos lados $A C em moldura superior fecha moldura$ , $A P em moldura superior fecha moldura$ e $M P em moldura superior fecha moldura$ do lote I, nem a medida de $B P em moldura superior fecha moldura$ do lote II.

Para começar, podemos encontrar o valor da medida do lado $A C em moldura superior fecha moldura$ , aplicando o teorema de Pitágoras, ou seja:

$100 ao quadrado igual a 80 ao quadrado mais A C em moldura superior fecha moldura ao quadrado 10000 igual a 6400 mais A C em moldura superior fecha moldura ao quadrado A C em moldura superior fecha moldura ao quadrado igual a 10000 menos 6400 A C em moldura superior fecha moldura ao quadrado espaço igual a 3600 A C em moldura superior fecha moldura igual a raiz quadrada de 3600 igual a 60 espaço m$

Poderíamos também encontrar esse valor observando que temos um múltiplo do triângulo pitagórico 3, 4 e 5.

Sendo assim, se um lado mede 80 m (4 . 20), o outro mede 100 m (5 . 20) , então o terceiro lado só poderá medir 60 m (3 . 20).

Sabemos que a cerca é a mediatriz da hipotenusa, portanto divide este lado em duas partes com mesma medida, formando um ângulo de 90º com o lado. Desta forma, o triângulo PMB é retângulo.

Note que os triângulos PMB e ACB são semelhantes, pois apresentam ângulos com mesma medida. Chamando o lado $A P espaço em moldura superior fecha moldura$ de x, temos que o lado $P B em moldura superior fecha moldura$ será igual a 80-x.

Sendo assim, podemos escrever as seguintes proporções:

$numerador 100 sobre denominador 80 menos x fim da fração igual a 80 sobre 50 80 menos x igual a numerador 50.100 sobre denominador 80 fim da fração 80 menos x igual a 125 sobre 2 x igual a 80 menos 125 sobre 2 x igual a numerador 160 menos 125 sobre denominador 2 fim da fração x igual a 35 sobre 2$

Falta ainda encontrar a medida do lado $P M em moldura superior fecha moldura$ . Para encontrar esse valor, vamos chamar esse lado de y. Por semelhança de triângulos, encontramos a seguinte proporção:

$50 sobre y igual a 80 sobre 60 y igual a numerador 60.50 sobre denominador 80 fim da fração y igual a 3000 sobre 80 y igual a 75 sobre 2$

Agora que conhecemos a medida de todos os lados, podemos calcular os perímetros dos lotes:

$p com I subscrito igual a 60 mais 50 mais 35 sobre 2 mais 75 sobre 2 p com I subscrito igual a numerador 120 mais 100 mais 35 mais 75 sobre denominador 2 fim da fração p com I subscrito igual a 330 sobre 2 igual a 165 espaço m$

Antes de calcular o perímetro do lote II, perceba que a medida de $P B em moldura superior fecha moldura$ será igual a $80 menos 35 sobre 2$ , ou seja $125 sobre 2$ . Desta maneira, o perímetro será:

$p com I I subscrito fim do subscrito igual a 50 mais 75 sobre 2 mais 125 sobre 2 p com I I subscrito fim do subscrito igual a numerador 100 mais 75 mais 125 sobre denominador 2 fim da fração p com I I subscrito fim do subscrito igual a 300 sobre 2 igual a 150 espaço m$

Assim, a razão entre os perímetros será igual a:

$p com I subscrito sobre p com I I subscrito fim do subscrito igual a 165 sobre 150 igual a 11 sobre 10$

Alternativa: d) $11 sobre 10$

2) Enem - 2013

Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

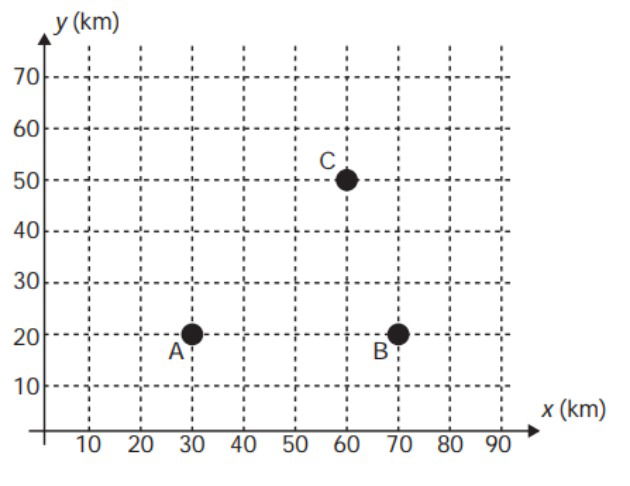
A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas

a) (65 ; 35).
b) (53 ; 30).
c) (45 ; 35).
d) (50 ; 20).
e) (50 ; 30).

Ver Resposta

Como queremos que a torre seja construída em um local equidistante das três antenas, ela deverá estar situada em algum ponto pertencente a mediatriz da reta AB, conforme representado na imagem abaixo:

Pela imagem, concluímos que a abscissa do ponto será igual a 50. Agora, precisamos encontrar o valor da ordenada. Para isso, vamos considerar que a distância entre os pontos AT e AC são iguais:

$d com a vírgula t subscrito fim do subscrito igual a d com t vírgula c subscrito fim do subscrito raiz quadrada de parêntese esquerdo 30 menos 50 parêntese direito ao quadrado mais parêntese esquerdo 20 menos y parêntese direito ao quadrado fim da raiz igual a raiz quadrada de parêntese esquerdo 50 menos 60 parêntese direito ao quadrado mais parêntese esquerdo y menos 50 parêntese direito ao quadrado fim da raiz 400 mais 400 menos 40 y mais y ao quadrado igual a 100 mais y ao quadrado menos 100 y mais 2500 100 y menos 40 y igual a 2600 menos 800 60 y igual a 1800 y igual a 30$

Alternativa: e) (50 ; 30)

Leia mais sobre alguns temas relacionados:

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações