Semelhança de Triângulos

Rosimar Gouveia

Professora de Matemática e Física

Dois triângulos são semelhantes quando possuem os três ângulos ordenadamente congruentes (mesma medida) e os lados correspondentes proporcionais. Usamos o símbolo ~ para indicar que dois triângulos são semelhantes.

Para saber quais são os lados proporcionais, primeiro devemos identificar os ângulos de mesma medida. Os lados homólogos (correspondentes) serão os lados opostos a esses ângulos.

Razão de Proporcionalidade

Como nos triângulos semelhantes os lados homólogos são proporcionais, o resultado da divisão desses lados será um valor constante. Esse valor é chamado de razão de proporcionalidade.

Considere os triângulos ABC e EFG semelhantes, representados na figura abaixo:

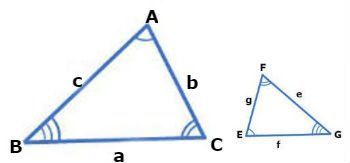
Os lados a e e, b e g, c e f são homólogos, sendo assim, temos as seguintes proporções:

Onde k é a razão de proporcionalidade.

Leia também sobre Razão e Proporção.

Casos de Semelhança

Para identificar se dois triângulos são semelhantes, basta verificar alguns elementos.

1º Caso: Dois triângulos são semelhantes se dois ângulos de um são congruentes a dois do outro. Critério AA (Ângulo, Ângulo).

2º Caso: Dois triângulos são semelhantes se os três lados de um são proporcionais aos três lados do outro. Critério LLL (Lado, Lado, Lado).

3º Caso: Dois triângulos são semelhantes se possuem um ângulo congruente compreendido entre lados proporcionais. Critério LAL (Lado, Ângulo, Lado).

Teorema Fundamental da semelhança

Quando uma reta paralela a um lado de um triângulo intersecta os outros dois lados em pontos distintos, forma um triângulo que é semelhante ao primeiro.

Na figura abaixo, representamos o triângulo ABC e a reta r paralela ao lado .

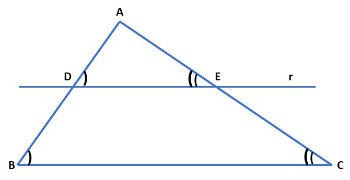
Observando a figura, notamos que os ângulos são congruentes, assim como os ângulos , pois a reta r é paralela ao lado . Assim, pelo critério AA, os triângulos ABC e ADE são semelhantes.

Leia também sobre Teorema de Tales e Teorema de Tales - Exercícios.

Relações Métricas no Triângulo Retângulo

Os triângulos que possuem um ângulo igual a 90º são chamados de triângulos retângulos. O lado oposto ao ângulo de 90º é chamado hipotenusa e os outros dois lados são chamados de catetos.

No triângulo representado abaixo, o lado a é a hipotenusa e b e c são os catetos.

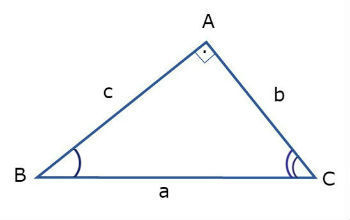
Ao traçar a altura relativa à hipotenusa, dividimos o triângulo retângulo em dois outros triângulos retângulos. Conforme figura abaixo:

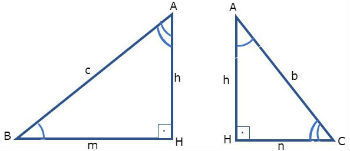
Observando os medidas dos ângulos desses três triângulos, percebemos que eles são semelhantes, ou seja:

.

Usando as proporções entre os lados, determinamos as seguintes relações:

Essas relações são muito importantes e são chamadas de relações métricas no triângulo retângulo.

Para saber mais sobre triângulos, leia também:

• Triângulo: tudo sobre este polígono
• Soma dos ângulos internos de um triângulo
• Triângulo Retângulo
• Classificação dos Triângulos
• Triângulo Isósceles
• Triângulo Escaleno
• Triângulo Equilátero
• Perímetro do Triângulo
• Área do Triângulo
• Exercícios de Matemática 8º ano

Congruência de Triângulos

Triângulos semelhantes não são triângulos iguais. Os triângulos são considerados congruentes (iguais) quando coincidem ao serem sobrepostos.

Casos de congruência de triângulos

Dois triângulos são congruentes quando for verificado um dos seguintes casos:

1º caso: Os três lados são respectivamente congruentes.

2º caso: Dois lados congruentes (mesma medida) e o ângulo formado por eles também congruente.

3º caso: dois ângulos congruentes e o lado compreendido entre eles congruente.

Exercícios

1) Dados os triângulos abaixo, responda:

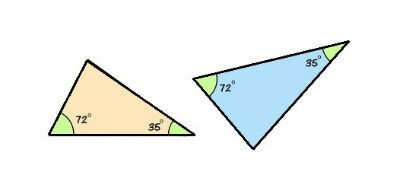
a) Eles são semelhantes? Justifique a resposta.
b) Qual é o ângulo que não aparece nas figuras?

2) Enem-2013

O dono de um sítio pretende colocar uma haste de sustentação para melhor firmar dois postes de comprimentos iguais a 6 m e 4 m. A figura representa a situação real na qual os postes são descritos pelos segmentos AC e BD e a haste é representada pelo segmento EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço que serão instalados.

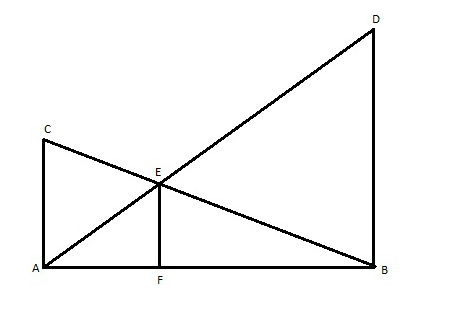
Qual deve ser o valor do comprimento da haste EF?

a) 1 m
b) 2 m
c) 2,4 m
d) 3 m
e) 2 √6 m

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.