Exercícios de Matemática para 8º ano (com respostas explicadas)
Estude com os exercícios de matemática para o 8º ano resolvidos. Uma lista com exercícios de todos os conteúdos de matemática que você estuda no colégio, com respostas e explicados passo a passo.
Os exercícios de matemática são alinhados à BNCC, todos com o código das habilidades para que os professores possam utilizar em suas aulas e planejamentos.
Exercício 1 (Potência e notação científica)
Habilidade BNCC EF08MA01
A astronomia estuda distâncias tão grandes que uma unidade de comprimento bem especial é utilizada: o ano-luz. Um ano-luz é a distância percorrida pela luz durante um ano e, no vácuo, corresponde, aproximadamente, a .
A estrela Epsilon Crucis faz parte da constelação do Cruzeiro do Sul e está a da Terra. A distância em anos-luz, entre esta estrela e a Terra é de, aproximadamente
anos-luz.
anos-luz.
anos-luz.
anos-luz.
Para descobrir quantos anos-luz cabem na distância entre a Terra e a Epsilon Crucis, dividimos o comprimento maior pelo menor.
Para realizar a divisão, dividimos os decimais do numerador e denominador e, para dividir as potências, como possuem a mesma base, repetimos a base e subtraímos os expoentes.
Para escrever em notação científica, deixamos um algarismo apenas antes da vírgula, diferente de zero.
Ao aumentar o número, deslocando a vírgula para a direita, deve-se reduzir o expoente em uma unidade.
O que equivale a 5,8 . 10 = 58.
A distância entre a Terra e a Epsilon Crucis, é de cerca de 58 anos-luz.
Veja notação científica e exercícios de notação científica.
Exercício 2 (Raiz e potência de expoente fracionário)
Habilidade BNCC EF08MA02
As seguintes potências com expoentes fracionários podem ser representadas na forma de raízes.
e
Suas soluções são, respectivamente
2 e 5.
2 e 8.
4 e 6.
2 e 6.
Para transformar uma potência com expoente fracionário em uma raiz, o denominador se transforma no índice da raiz e o numerador o expoente do radicando.
Veja potenciação e radiciação.
Exercício 3 (Princípio multiplicativo da contagem)
Habilidade BNCC EF08MA03
Uma rede social está aumentando muito rápido o número de usuários e, recentemente, resolveu melhorar a segurança, protegendo os perfis de seus usuários. Até então, para criar uma conta era necessária uma senha com seis dígitos, utilizando os algarismos de 0 a 9 sem repetição. Agora, é preciso cadastrar no lugar do primeiro dígito, uma letra do alfabeto, incluindo y, w e k. A única restrição é que esta letra deve ser o primeiro dígito da senha.
A diferença entre o número de senhas possíveis antes da inovação de segurança e depois, é de
937 440.
21 600 000.
635 040.
21.
Número de senhas antes da mudança.
Para escolha do primeiro dígito há 10 possibilidades, os algarismos de 0 a 9.
Para a escolha do segundo dígito há 9 possibilidades, pois um já foi escolhido para ocupar a primeira posição, e não pode ser repetido.
Seguindo este raciocínio até o sexto dígito e multiplicando as possibilidades para cada escolha, temos:
10 . 9 . 8 . 7 . 6 . 5 = 151 200 senhas possíveis.
Número de senhas após a mudança.
Para escolha do primeiro dígito há 26 possibilidades, as letras.
Para escolha do segundo dígito há 10 possibilidades, um algarismo entre 0 e 9.
Para escolha do terceiro dígito há 9 possibilidades, pois um já foi escolhido.
Seguindo o raciocínio até ocupar o sexto dígito, temos:
26 . 10 . 9 . 8 . 7 . 6 = 786 240 senhas possíveis.
Diferença
786 240 - 151 200 = 635 040
Veja princípio fundamental da contagem.
Exercício 4 (Porcentagem)
Habilidade BNCC EF08MA04
Em uma loja um aparelho de som que custava R$ 800,00 teve um desconto de 17% para pagamento à vista. O cliente que decidir comprar o equipamento nestas condições pagará
R$136,00.
R$783,00.
R$690,00.
R$664,00.
Há dois modos de realizar o cálculo.
1º modo: calcular o desconto e subtrair do total.
Descontando do valor total:
800 - 136 = 664
2º modo: multiplicar pelo decimal que representa a sobra percentual, depois do desconto.
Como o desconto é de 17% e o preço inicial representa 100%, temos:
100% - 17% = 83%
83% em decimal é 0,83.
Multiplicando pelo valor total:
0,83 x 800 = 664
Assim, um cliente que decidir pagar à vista, pagará a quantia de R$664,00.
Veja mais sobre:
Exercício 5 (Dízima periódica e fração geratriz)
Habilidade BNCC EF08MA05
Alguns números possuem infinitas casas decimais que se repetem, são as dízimas periódicas. Uma dízima periódica pode ser gerada por uma divisão entre números inteiros. Em outras palavras, uma dízima pode ser representada na forma de sua fração geratriz.
Diante disto, o resultado da multiplicação entre 1,3333... e 1,1666..., na forma de sua fração geratriz irredutível é
9/4.
4/3.
14/9.
28/18.
Para 1,3333...
Usando o método da equação, o objetivo é deixar apenas a dízima após a vírgula, utilizando multiplicações.
Subtraindo a equação I da II:
Isolando o x
Simplificando
Para 1,1666...
Precisamos de mais uma equação em que reste apenas a dízima após a vírgula, para isso, multiplicamos a equação I por 100.
Subtraindo a equação II da III
Isolando o x
Simplificando por 5 e depois por 3:
Multiplicando os resultados.
Escrevendo na forma irredutível.
Veja sobre:
Exercício 6 (Valor numérico de expressões algébricas)
Habilidade BNCC EF08MA06
Uma expressão algébrica é uma sequência de operações que envolvem letras e números. Uma vez que, a cada incógnita (letra) um valor numérico é associado, é possível descobrir o valor numérico da expressão.
A expressão algébrica , com a = 2 e b = 3, possui valor numérico igual a
8.
12.
-8.
72.
1º passo: substituir as letras pelos seus valores numéricos.
2º passo: resolver as potências.
3º passo: resolver as multiplicações e divisões.
4º passo: resolver adições e subtrações.
O valor numérico associado a expressão é -8.
Exercício 7 (Equação linear de 1º grau e sua representação no plano cartesiano)
Habilidade BNCC EF08MA07
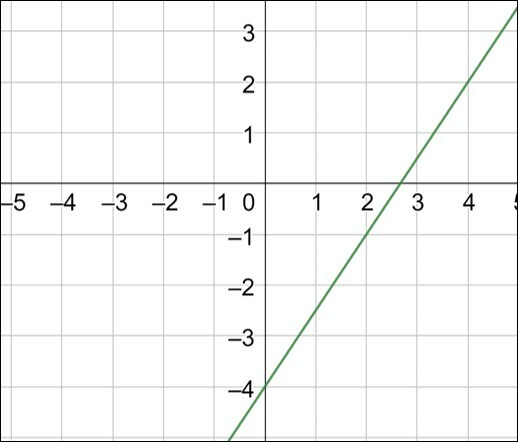
A representação no plano cartesiano da equação 3x + 2y = 8 é
 .
.
 .
.
 .
.
 .
.
Para representar a equação no plano cartesiano, devemos obter pelo menos dois pares ordenados.
Sabemos que a equação é linear, pois os expoentes das incógnitas são iguais a 1. Lembre-se que o expoente igual a 1 pode ficar omitido.
Arbitrando valores para x, encontramos valores respectivos para o y.
| x | 3x + 2y = 8 | y |
|---|---|---|
| 0 | 4 | |
| 2 | 1 |
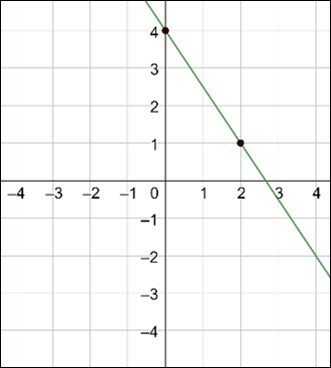
Escolhendo os valores 0 e 2 para x, obtemos os respectivos valores 4 e 1 para y. Os pares ordenados encontrados são (0, 4) e (2, 1).
Localizando estes pontos no plano e traçando uma reta entre eles, temos:
Veja também:
Exercício 8 (Sistema de equações polinomiais de 1º grau)
Habilidade BNCC EF08MA08
Maurício comprou 4 blusas e 2 calças gastando 220 reais. Seu irmão Joaquim gostou dos preços e comprou 3 blusas e 4 calças, gastando 290 reais. No dia seguinte, ao chegar à escola seus amigos lhes perguntaram quanto pagaram por cada blusa e cada calça. Os valores unitários das blusas e das calças são, respectivamente
R$35,00 e R$50,00.
R$40,00 e R$30,00.
R$30,00 e R$50,00.
R$25,00 e R$35,00.
Equação da compra de Maurício.
4 blusas + 2 calças = 220
4b + 2c = 220
Equação da compra de Joaquim.
3 blusas e 4 calças = 290
3b + 4c = 290
Como temos duas equações e duas incógnitas (preço da blusa e da calça) montamos um sistema.
Para resolver o sistema existem alguns métodos, um deles o da adição.
Para isto, multiplicamos a equação I por -2.
O segundo passo é somar as equações I e II.
Assim, o resultado da soma é:
-5b = -150
Isolando b, temos:
Uma vez que temos o valor de b, o substituímos em outra equação, como a equação II.
Desta forma, o preço de cada blusa é de R$30,00 e, cada calça R$50,00.
Veja Sistemas de Equações do 1º Grau - Exercícios.
Exercício 9 (Equação polinomial de 2º grau)
Habilidade BNCC EF08MA09
No projeto de uma casa, um mosaico será construído no chão de uma sala com peças de cerâmicas quadrangulares de medida lateral igual a x cm. Se a área ocupada por este mosaico é de 0,36 m² e serão utilizadas 9 peças, a medida x de cada peça de revestimento, em centímetros, é igual a
60 cm.
40 cm.
36 cm.
20 cm.
Como as peças são quadradas a área de cada uma é igual a x . x = x².
Sendo 9 peças temos 9x² de área total, iguais a 0,36 m².
Transformando para centímetros quadrados, temos 3600 cm². Assim,
Assim, cada peça possui 20 cm de lateral.
Exercício 10 (Sequência não recursiva)
Habilidade BNCC EF08MA10
Uma sequência é não recursiva quando seus elementos não dependem do valor do termo anterior, mas sim de sua posição na sequência. Considere n como a posição de um termo qualquer na sequência.
Exemplo: é o primeiro termo,
é o segundo,
é o terceiro e
é um termo genérico qualquer.
Em uma sequência formada por , os termos 7, 8 e 9 são, respectivamente:
148, 193 e 244.
43, 49 e 55.
115, 201e 256.
22, 25 e 28.
Para a7
Para a8
Para a9
Assim, os termos 7, 8 e 9 são: 148, 193 e 244.
Exercício 11 (Sequência recursiva)
Habilidade BNCC EF08MA11
Sendo n o índice que indica a ordem dos elementos em uma sequência, analise o algoritmo que define a sequência:
- Início da sequência;
- Seus termos valem 1 se n é 1 ou 2;
- Se n é maior que 2 o termo é a soma entre seu anterior e o anterior do anterior.
- A sequência termina em n=6.
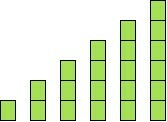
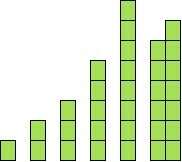
A opção que representa graficamente a sequência é
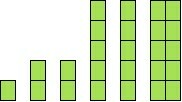
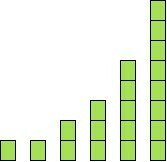
Para n=1, a1 = 1
Para n=2, a2 = 1
Para n=3, a3 = a1 + a2 = 1 + 1 = 2 (Aqui n é maior que 2 e é a soma dos dois anteriores).
Para n=4, a4 = a3 + a2 = 2 + 1 = 3 (Anterior e anterior do anterior).
Para n=5, a5 = a4 + a3 = 3 + 2 = 5
Para n=6, a6 = a5 + a4 = 5 + 3 = 8
Numericamente a sequência é:
(1, 1, 2, 3, 5, 8)
Graficamente, temos:
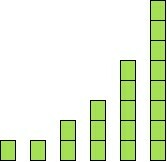
Exercício 12 (Variação de duas grandezas: diretamente, inversamente, ou não proporcionais)
Habilidade BNCC EF08MA12
As seguintes relações:
- A quantidade de tecido para produzir camisas e o número de camisas produzidas.
- O tempo para um trem se deslocar entre duas cidades e a velocidade deste trem.
- A área de um quadrado e o comprimento de seus lados.
Representam grandezas, respectivamente:
Diretamente, inversamente e não proporcionais.
Diretamente, Diretamente e inversamente proporcionais.
Inversamente, diretamente e não proporcionais.
Inversamente, não proporcionais e diretamente proporcionais.
A quantidade de tecido para produzir camisas e o número de camisas produzidas.
Mais tecido, mais camisas.
Menos tecido, menos camisas.
Esta é uma relação diretamente proporcional.
O tempo para um trem se deslocar entre duas cidades e a velocidade deste trem.
Maior velocidade, menor tempo de viagem.
Menor velocidade, maior tempo de viagem.
Esta relação é inversamente proporcional.
A área de um quadrado e o comprimento de seus lados.
A área de um quadrado aumenta com o expoente 2 (elevado ao quadrado) do comprimento do lado.
A área de um quadrado é: l x l = l² , sendo l a medida do lado.
A representação de uma função l² é uma parábola, portanto, não é proporcional.
Veja grandezas proporcionais.
Exercício 13 (Cálculo com grandezas diretas ou inversas)
Habilidade BNCC EF08MA13
Em uma receita de bolo estão indicadas as seguintes quantidades dos ingredientes:
- 9 xícaras de farinha de trigo;
- 3 ovos;
- 600 ml leite;
- 6 colheres de sopa de açúcar;
- 3 colheres de chá de fermento.
A senhora Eleonora ao fazer um bolo no domingo à tarde, verificou ter pouco trigo, apenas 3 xícaras e, para adaptar a receita irá utilizar
1 ovo, 200 ml de leite, 2 colheres de sopa de açúcar e 1 colher de chá de fermento.
1 ovo, 300 ml de leite, 2 colheres de sopa de açúcar e 3 colher de chá de fermento.
1 ovo, 200 ml de leite, 2 colheres de sopa de açúcar e 3 colher de chá de fermento.
1 ovo, 600 ml de leite, 4 colheres de sopa de açúcar e 1 colher de chá de fermento.
A relação entre as grandezas é diretamente proporcional, visto que ao diminuir uma, as outras devem diminuir proporcionalmente.
Usando uma regra de três:
Ovos
9 xícaras de farinha de trigo estão para 3 ovos, assim como, 3 xícaras de farinha de trigo estão para x.
Pela propriedade fundamental das proporções, multiplicamos os extremos pelos meios:
Assim, utilizando 3 xícaras de farinha de trigo, deverá ser usado um ovo.
Para os demais ingredientes:
Leite
Açúcar
Fermento
Veja proporções.
Exercício 14 (Congruência de triângulos)
Habilidade BNCC EF08MA14
Dentre os triângulos abaixo identifique os pares de semelhantes e os casos de semelhança.

A e C. Caso AA
C e B. Caso LAL
D e C. Caso LLL
A e D. Caso AA
O par de triângulos C e B são semelhantes pelo caso LAL (lado-ângulo-lado)
Lado 6
Ângulo d
Lado 8
Veja congruência de triângulos.
Exercício 15 (Construções geométricas de ângulos e polígonos regulares)
Habilidades BNCC EF08MA15, EF08MA16 e EF08MA17
A partir de um ponto O é traçado um segmento de reta até um ponto M que faz um ângulo de 90º com outro segmento. O segmento OM além de ser uma mediatriz, também é bissetriz de um ângulo de 60º em O.
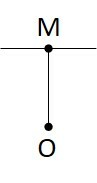
A partir do segmento OM, girando 60º no sentido horário, outra mediatriz/bissetriz é traçada, iniciando no ponto O e indo até um ponto N, por onde também passa outro segmento perpendicular. Desse modo, os segmentos perpendiculares a OM e ON respectivamente, se tocam em um mesmo ponto.
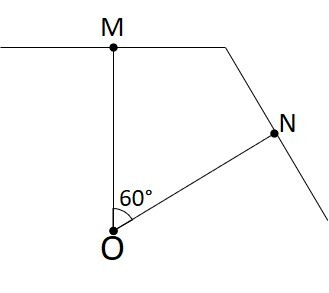
A retas mediatrizes/bissetrizes possuem o mesmo comprimento entre si, assim como os segmentos perpendiculares.
Este processo continua até que um polígono é formado. Este polígono é um
pentágono.
hexágono.
heptágono.
quadrilátero.
A partir do segmento OM, um segmento ON é traçado 60º no sentido horário. Como um ponteiro de um relógio, outros segmentos são adicionados.
60º de OM para ON;
60º de ON para o próximo; (60º + 60º = 120º);
Assim por diante, de modo que:
60º + 60º + 60º + 60º + 60º + 60º = 360º
Conclui-se que são traçadas seis retas mediatrizes. Como a cada mediatriz um segmento perpendicular é traçado e, estes se tocam, temos uma figura com seis lados, um hexágono.
Exercício 17 (Transformações geométricas: reflexão, translação e rotação)
Habilidade EF08MA18
No plano cartesiano é representado o seguinte polígono:

Após passar pelas transformações geométricas:
- 1 reflexão em relação ao eixo x;
- 1 uma translação de -4 unidades no eixo x;
- 1 reflexão em relação ao eixo x;
- 1 rotação de 90º no sentido horário ao redor de seu vértice V.
O polígono está representado pela opção:
1
1
1
1
1 reflexão em relação ao eixo x;
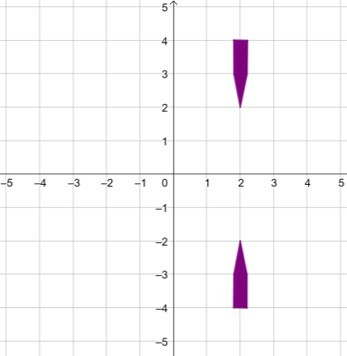
1 uma translação de -4 unidades no eixo x;
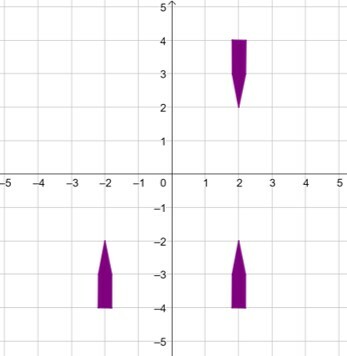
1 reflexão em relação ao eixo x;
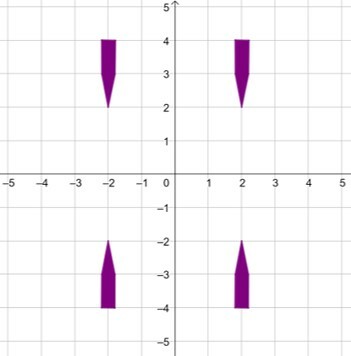
1 rotação
Exercício 18 (Área de polígonos e círculo)
Habilidade EF08MA19
Em uma praça será construída uma grande rosa-dos-ventos no chão e, estará inscrita em um círculo.
Para desenhá-la, um triângulo isósceles foi inscrito na circunferência como na imagem abaixo.
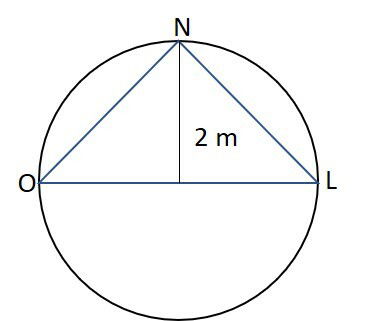
A mediatriz M deste triângulo em relação ao segmento OL (oeste-leste) possui 2 metros.
Uma cópia do triângulo NOL sofrerá uma reflexão em relação às direções leste e oeste, formando o triângulo OLS, de modo a produzir a região da praça onde ficará a rosa-dos-ventos. O piso desta região será pintado de azul, enquanto a área que completa o círculo, de vermelho.
Considere = 3.
A medida da superfície pintada de vermelho é
16 m².
4 m².
8 m²
2 m².
A figura completa é:
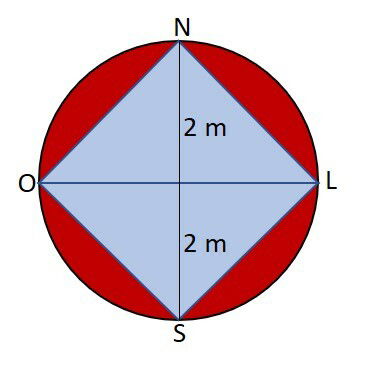
A área interior é formada por dois triângulos isósceles, portanto, é um quadrado. A área de um quadrado é calculada por:
A área do círculo é calculada por:
Percebemos que o raio r do círculo é a própria mediatriz M (segmento que intercepta outro segmento ao meio, fazendo 90º).
A área pretendida é a área do círculo menos a do quadrado, de forma que:
Como o raio é igual à mediatriz, r = M.
Temos o comprimento da mediatriz, precisamos do lado do quadrado.
Pelo teorema de Pitágoras:
Assim, podemos substituir na equação anterior:
Colocando M² em evidência:
Substituindo os valores de M e .
Conclusão
A área vermelha no círculo possui 4m².
Veja mais sobre:
Exercício 19 (Volume de bloco retangular e medidas de capacidade)
Habilidades BNCC EF08MA20 e EF08MA21
Uma cisterna na forma de um prisma quadrangular, com medidas de 9 m de comprimento, 5 m de largura e 2 m de altura, foi construída para captar a água da chuva recolhida pelos telhados de um condomínio. Esta cisterna poderá armazenar, em sua capacidade máxima
90 l.
16 000 l.
90 000 l.
16 l.
Objetivo
Determinar a quantidade de água em litros que a cisterna pode armazenar.
1º passo: determinar o volume em metros cúbicos.
Como as medidas já estão em metros, basta multiplicar os valores das três dimensões.
A cisterna possui 90 metros cúbicos de volume.
2 º passo: determinar quantos litros cabem neste volume.
1 m³ armazena 1000 litros. Assim, 90 m³ = 90 . 1000 = 90 000 l
Veja mais sobre:
Exercício 20 (Princípio multiplicativo e soma das probabilidades de um espaço amostral)
Habilidades BNCC EF08MA22
Considere o experimento lançar um dado duas vezes consecutivas e somar os resultados obtidos no 1º e no 2º lançamento. A probabilidade de sair uma soma maior que oito e a probabilidade do evento complementar são, respectivamente,
80,2% e 19,8%.
27,7% e 72,3%.
17,5% e 82,5%.
33% e 66%.
1º passo: calcular a probabilidade da soma ser maior que oito.
Probabilidade é a razão entre o número de casos favoráveis ao evento e o número total de casos possíveis no espaço amostral.
Sendo o experimento aleatório lançar um dado duas vezes consecutivas e anotar os resultados, o número de elementos no espaço amostral é 6 . 6 = 36 (possibilidades do primeiro dado e possibilidades do segundo).
Dentre os 36 casos possíveis, 10 resultam em soma maior que oito.
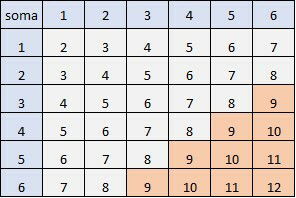
Este é o número de casos favoráveis ao evento A, sair soma maior que oito. Assim, a probabilidade da soma dos resultados dos dois lançamentos ser maior que 8 é:
2º passo: calcular a probabilidade do evento complementar.
Probabilidade é um número entre 0 e 1, ou 0% e 100%. O evento complementar é o quanto falta para completar 1 ou, 100%.
No caso desta situação-problema só há duas possibilidades, ou a soma é maior que oito (27,7%), ou a soma é menor que oito. Neste caso, o evento complementar é a soma ser menor que oito.
Assim, a probabilidade da soma ser menor que oito é de 72,3%.
Veja mais sobre:
Exercício 21 (Tipos de gráficos e organização de dados)
Habilidades BNCC EF08MA23 e EF08MA24
O gráfico a seguir representa as alturas dos alunos do ensino fundamental de um colégio em centímetros. No eixo horizontal estão os intervalos das alturas em centímetros. Acima se encontram as quantidades de alunos com altura naquele intervalo.

O tipo de gráfico e a variável estatística são, respectivamente:
de barras e variável quantitativa discreta.
histograma e variável quantitativa contínua.
de linhas e variável qualitativas nominais.
de setores e variável qualitativas ordinais.
O histograma é uma representação gráfica onde as frequências são dispostas em colunas.
As variáveis quantitativas são numeráveis. Sendo contínuas, pertencem a um conjunto infinito de valores sem interrupção entre eles.
As medidas de comprimento são contínuas, pois mesmo entre os centímetros existem infinitos valores fracionados como: milímetros, micrômetros, nanômetros ...
Exercício 22 (Média, moda e mediana)
Habilidade BNCC EF08MA25
Em uma escola, estes alunos de diferentes turmas foram selecionados para um recital de poesia:
- Alexandre: 8 anos
- Fabrício: 10 anos
- Carla: 12 anos
- Patrick: 15 anos
- João: 13 anos
- Eleonora: 12 anos
- Nicole: 10 anos
- Maria: 9 anos
Considerando suas idades, determine a média, a moda e a mediana.
Média = 11,125
Moda: 10 e 12
Mediana = 11
Média = 11,125
Moda: 9 e 10
Mediana = 10
Média = 9,25
Moda: 10
Mediana = 11
Média = 11,125
Moda: 10 e 12
Mediana = 11,125
Média
Moda
A moda ou, as modas, são os elementos que mais se repetem. Neste caso, os elementos 10 e 12 se repetem igualmente duas vezes cada. Portanto, as modas são 10 e 12.
Mediana
Para determinar a mediana das idades devemos escrever o rol de dados, a ordenação crescente ou decrescente.
8, 9, 10, 10, 12, 12, 13, 15
Como a quantidade de dados é par, a mediana é a média aritmética dos dados centrais.
Veja mais sobre:
Veja também:
- 27 exercícios de Matemática Básica
- Exercícios de Matemática 9º ano com respostas
- 23 exercícios de Matemática 7º ano
- Exercícios de Matemática 6º ano
ASTH, Rafael. Exercícios de Matemática para 8º ano (com respostas explicadas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-de-matematica-8-ano/. Acesso em:



