Medidas de Volume

Rosimar Gouveia

Professora de Matemática e Física

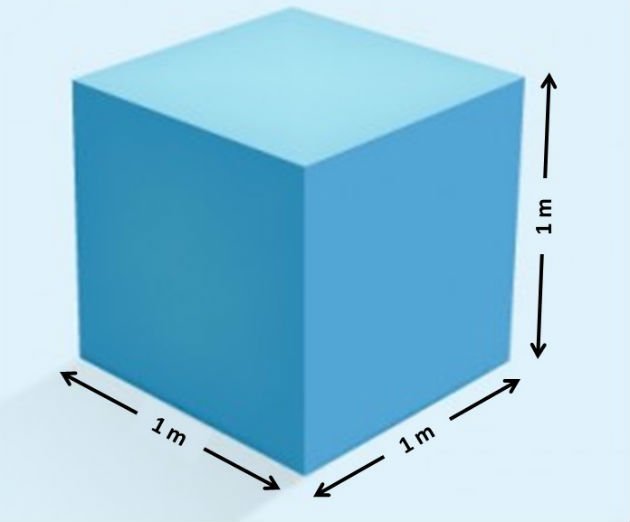
A medida de volume no sistema internacional de unidades (SI) é o metro cúbico (m³). Sendo que 1 m³ corresponde ao espaço ocupado por um cubo de 1 m de aresta.

Neste caso, o volume é encontrado multiplicando-se o comprimento, a largura e a altura do cubo.

Conversão de unidades

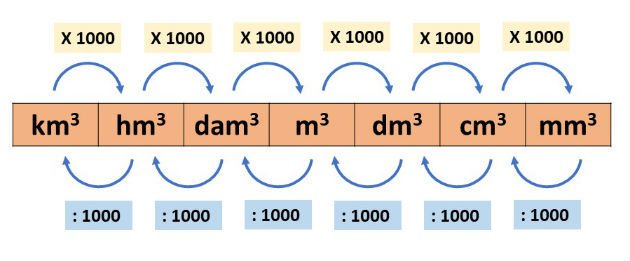
As unidades do sistema métrico decimal de volume são: quilômetro cúbico (km³), hectômetro cúbico (hm³), decâmetro cúbico (dam³), metro cúbico (m³), decímetro cúbico (dm³), centímetro cúbico (cm³) e milímetro cúbico (mm³).

As transformações entre os múltiplos e submúltiplos do m³ são feitas multiplicando-se ou dividindo-se por 1000.

Para transformar as unidades de volume, podemos utilizar a tabela abaixo:

Exemplos

1) Quantos centímetros cúbicos há em uma caixa que apresenta a forma de um cubo e que as medidas do seu comprimento, largura e altura são iguais a 0,3 m?

Solução

Como a caixa possui o formato cúbico, para encontrar seu volume, basta multiplicar suas dimensões. Assim, o volume será igual a:

V = 0,3 . 0,3 . 0,3 = 0,027 m³

Para transformar esse valor de m³ para cm³, devemos observar na tabela que será necessário multiplicar por 1000 duas vezes (primeiro passando de m³ para dm³ e depois de dm³ para cm³). Assim, temos:

V = 0,027 . 1000 . 1000 = 27 000 cm³

2) Uma lata de tinta possui um volume de 24 dm³. Qual o volume desta lata em metros cúbicos?

Solução

Para transformar de dm³ para m³ é necessário, conforme vemos na tabela acima, dividir o valor por 1000. Assim, a lata possui:

V = 24 : 1000 = 0,024 m³

Saiba mais sobre Conversão de Unidades.

Medida de capacidade

As medidas de capacidade representam o volume interno dos recipientes. Desta forma, podemos muitas vezes conhecer o volume de um determinado corpo enchendo-o com um líquido de volume conhecido.

A unidade de medida padrão de capacidade é o litro, sendo ainda utilizados seus múltiplos (kl, hl e dal) e submúltiplos (dl,cl e ml).

Em algumas situações é necessário transformar a unidade de medida de capacidade para uma unidade de medida de volume ou vice versa. Nestes casos, podemos utilizar as seguintes relações:

• 1 m³ = 1 000 L
• 1 L = 1 dm³

Exemplo

A piscina, representada na imagem abaixo, possui as seguintes dimensões: 7 m de comprimento, 4 m de comprimento e 1,5 m de altura. Quantos litros de água serão necessários para que a esta piscina fique completamente cheia?

Solução

Primeiro, precisamos calcular o valor do volume desta piscina. Para isso, vamos multiplicar a área da base pela altura da piscina. Assim, temos:

V = 7 . 4 . 1,5 = 42 m³

Agora que conhecemos seu volume, podemos utilizar as relações para descobrir sua capacidade. Para isso, podemos fazer uma regra de três.

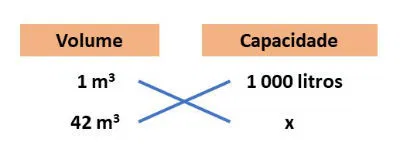
x = 42 . 1000 = 42 000

Portanto, a piscina ficará cheia quando estiver com 42 000 litros de água.

Outras unidades de volume

Além do metro cúbico e seus múltiplos, existem outras unidade de medidas de volume. Essas unidades são usadas principalmente em países de língua inglesa.

Polegada cúbica e pé cúbico são unidades usadas para volumes sólidos. Já a onça fluida, o pint, o quarto, o galão e o barril são unidades usadas para volumes líquidos.

Para saber mais, veja também:

• Sistema Internacional de Unidades
• Medidas de Capacidade
• Volume do cubo

Exercícios Resolvidos

1) Enem - 2017

Um empresa especializada em conservação de piscinas utiliza um produto para tratamento da água cujas especificações técnicas sugere que seja adicionado 1,5 mL desse produto para cada 1 000 L de água da piscina. Essa empresa foi contratada para cuidar de uma piscina de base retangular, de profundidade constante igual a 1,7 m, com largura e comprimento iguais a 3 m e 5 m, respectivamente. O nível da lâmina d’água dessa piscina é mantido a 50 cm da borda da piscina.

A quantidade desse produto, em mililitro, que deve ser adicionada a essa piscina de modo a atender às suas especificações técnicas é:

a) 11,25.
b) 27,00.
c) 28,80.
d) 32,25.
e) 49,50

2) Enem - 2017 (PPL)

Em alguns países anglo-saxões, a unidade de volume utilizada para indicar o conteúdo de alguns recipientes é a onça fluida britânica. O volume de uma onça fluida britânica corresponde a 28,4130625 mL.

A título de simplificação, considere uma onça fluida britânica correspondendo a 28 mL.

Nessas condições, o volume de um recipiente com capacidade de 400 onças fluidas britânicas, em cm³, é igual a

a) 11 200.
b) 1 120.
c) 112.
d) 11,2.
e) 1,12.

Adquira mais conhecimento com os conteúdos:

• Exercícios sobre unidades de medida resolvidos
• Medidas de Tempo
• Medidas de Massa
• Medidas de Comprimento
• Como Transformar Minutos em Horas
• Exercícios de Matemática 8º ano

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.