Equação da Reta

Rafael C. Asth

Professor de Matemática e Física

A equação da reta é uma lei matemática que determina um conjunto de pontos que formam uma reta, representada em um plano cartesiano (x, y).

Conhecendo as coordenadas de dois pontos distintos que pertençam à reta, podemos determinar sua equação.

Também é possível definir uma equação da reta a partir de sua inclinação e das coordenadas de um ponto que lhe pertença.

Equação geral da reta

Uma reta no plano pode ser representada pela equação:

Por exemplo:

2x + 3y + 4 = 0

Dois pontos definem uma reta. Desta forma, podemos encontrar a equação geral da reta fazendo o alinhamento de dois pontos com um ponto (x,y) genérico da reta.

Sejam os pontos A(x_a,y_a) e B(x_b,y_b), não coincidentes e pertencentes ao plano cartesiano.

Três pontos estão alinhados quando o determinante da matriz associada a esses pontos é igual a zero. Assim devemos calcular o determinante da seguinte matriz:

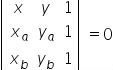
Desenvolvendo o determinante encontramos a seguinte equação:

(y_a - y_b) x + (x_b - x_a) y + x_ay_b - x_by_a = 0

Vamos chamar:

a = (y_a - y_b)
b = (x_b - x_a)
c = x_ay_b - x_by_a

A equação geral da reta é definida como:

ax + by + c = 0

Onde a, b e c são constantes e a e b não podem ser simultaneamente nulos.

Exemplo

Encontre uma equação geral da reta que passa pelos pontos A(-1, 8) e B(-5, -1).

Primeiro devemos escrever a condição de alinhamento de três pontos, definindo a matriz associada aos pontos dados e a um ponto genérico P(x,y) pertencente a reta.

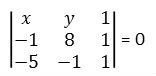
Desenvolvendo o determinante, encontramos:

(8+1)x + (1-5)y + 40 + 1 = 0

A equação geral da reta que passa pelos pontos A(-1,8) e B(-5,-1) é:

9x - 4y + 41 = 0

Para saber mais, leia também sobre Determinante.

Equação reduzida da reta

A equação reduzida da reta é da forma:

Onde,

x e y são pontos no plano;
m é o coeficiente angular (inclinação em relação ao eixo x);
n é o coeficiente linear (ponto onde a reta corta o eixo y).

Coeficiente angular

Podemos encontrar uma equação da reta r conhecendo a sua inclinação (direção), ou seja o valor do ângulo θ que a reta apresenta em relação ao eixo x.

Para isso associamos um número m, que é chamado de coeficiente angular da reta, tal que:

O coeficiente angular m também pode ser encontrado conhecendo-se dois pontos pertencentes a reta.

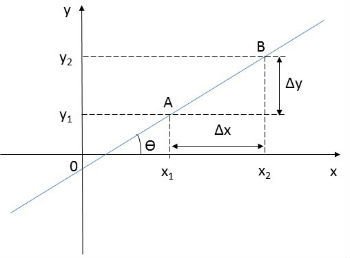
Como m = tg θ, então:

Exemplo

Determine o coeficiente angular da reta r, que passa pelos pontos A(1,4) e B(2,3).

Sendo,

x₁ = 1 e y₁ = 4
x₂ = 2 e y₂ = 3

Conhecendo o coeficiente angular da reta m e um ponto P₀(x₀,y₀) pertencente a ela, podemos definir sua equação.

Para isso substituímos na fórmula do coeficiente angular o ponto conhecido P₀ e um ponto P(x,y) genérico, também pertencente a reta:

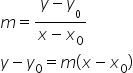
Exemplo

Determine uma equação da reta na forma reduzida que passa pelo ponto A(2,4) e tem coeficiente angular 3.

Para encontrar a equação da reta basta substituir os valores dados:

y - 4 = 3 (x - 2)
y - 4 = 3x - 6
-3x + y + 2 = 0

Coeficiente linear

O coeficiente linear n da reta r é definido como o ponto onde a reta intercepta o eixo y, ou seja o ponto de coordenadas P(0,n).

Utilizando esse ponto, temos:

y - n = m (x - 0)

y = mx + n (Equação reduzida da reta).

Exemplo

Sabendo que a equação da reta r é dada por y = x + 5, identifique seu coeficiente angular, sua inclinação e o ponto em que a reta intercepta o eixo y.

Como temos a equação reduzida da reta, então:

m = 1
Sendo m = tg θ ⇒ tg θ = 1 ⇒ θ = 45º
O ponto de interseção da reta com o eixo y é o ponto P(0,n), sendo n=5, então o ponto será P(0,5)

Leia também Cálculo do coeficiente angular

Equação segmentária da reta

A equação segmentária da reta é:

Onde:
p é o ponto onde a reta corta o eixo x (p, 0);
q é o ponto onde a reta corta o eixo y (0,q).

Podemos calcular o coeficiente angular usando o ponto A(a,0) que a reta intercepta o eixo x e o ponto B(0,b) que intercepta o eixo y:

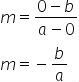
Considerando n = b e substituindo na forma reduzida, temos:

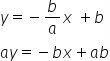
Dividindo todos os membros por ab, encontramos a equação segmentária da reta:

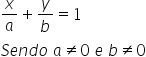
Exemplo

Escreva, na forma segmentária, a equação da reta que passa pelo ponto A(5,0) e tem coeficiente angular 2.

Primeiro encontramos o ponto B(0,b), substituindo na expressão do coeficiente angular:

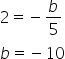
Substituindo os valores na equação, temos a equação segmentária da reta:

Veja também Retas Perpendiculares.

Exercícios sobre equação da reta resolvidos

Exercício 1

Escreva a equação da reta 2x + y + 3 = 1 , na forma reduzida.

Exercício 2

Determine a equação da reta que passa pelo ponto (3, 2) e possui coeficiente angular igual a 2.

Exercício 3

Dada a reta com a equação 2x + 4y = 9 , determine seu coeficiente angular.

Exercício 4

Escreva a equação da reta 3x + 9y - 36 = 0 na forma reduzida.

Exercício 5

(ENEM - 2016) Para uma feira de ciências, dois projéteis de foguetes, A e B, estão sendo construídos para serem lançados. O planejamento é que eles sejam lançados juntos, com o objetivo de o projétil B interceptar o A quando esse alcançar sua altura máxima. Para que isso aconteça, um dos projéteis descreverá uma trajetória parabólica, enquanto o outro irá descrever uma trajetória supostamente retilínea. O gráfico mostra as alturas alcançadas por esses projéteis em função do tempo, nas simulações realizadas.

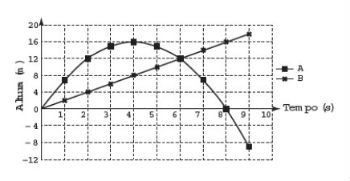
Com base nessas simulações, observou-se que a trajetória do projétil B deveria ser alterada para que o
objetivo fosse alcançado.

Para alcançar o objetivo, o coeficiente angular da reta que representa a trajetória de B deverá
a) diminuir em 2 unidades.
b) diminuir em 4 unidades.
c) aumentar em 2 unidades.
d) aumentar em 4 unidades.
e) aumentar em 8 unidades.

Leia também sobre:

• Exercícios sobre equação da reta resolvidos
• Geometria analítica
• Plano Cartesiano
• Distância entre dois pontos
• Reta
• Segmento de Reta

Veja também: Exercícios sobre Geometria Analítica

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.