Retas perpendiculares: o que são e como identificar (com exemplos e exercícios)

Rafael C. Asth

Professor de Matemática e Física

Adicionar aos favoritos Salvar Adicionar aos favoritos

Retas perpendiculares são duas linhas que se encontram formando um ângulo reto (90 graus). É fácil lembrar disso pensando nos cantos de uma folha de papel ou no formato da letra "L".

Na geometria analítica, usamos a inclinação (coeficiente angular, chamado de "m") para saber se duas linhas são perpendiculares.

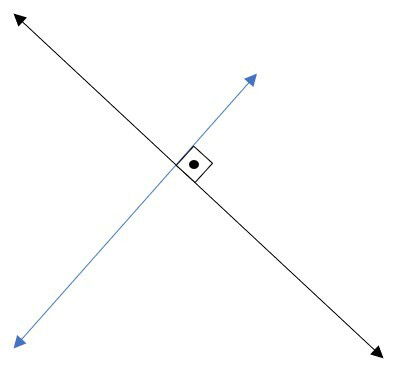
Utilizamos o símbolopara indicar que duas retas são perpendiculares e podemos identificá-las analisando a relação entre seus coeficientes angulares.

O coeficiente angular (m) indica a inclinação de uma reta. Quanto maior o valor de m, mais inclinada será a reta. Para calcular a inclinação entre dois pontos (x₁, y₁) e (x₂, y₂), usamos a fórmula: .

As retas podem ser representadas por equações. Neste caso, podemos determinar se duas retas são perpendiculares mesmo sem visualizar a imagem, apenas verificando elementos em suas equações.

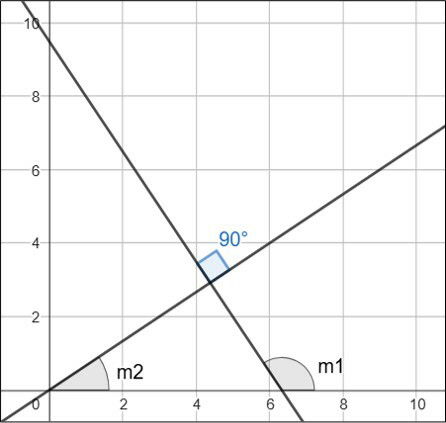
O que é o coeficiente angular e sua relação com a perpendicularidade

O coeficiente angular (m) de uma reta é o número que indica sua inclinação. Para duas retas serem perpendiculares, o produto de seus coeficientes angulares deve ser igual a −1.

Uma reta r de coeficiente angular e uma reta s de coeficiente angular , serão perpendiculares se:

Você pode se interessar por relembrar coeficiente angular.

Exemplo de verificação de retas perpendiculares:
Determine a equação da reta s que passa pelo ponto P (1,4) e é perpendicular à reta r cuja equação é x - y - 1 = 0.

Resolução:
Primeiro, encontraremos o coeficiente angular da reta r isolando y do lado esquerdo.

y = x - 1

Com a equação na forma reduzida, o coeficiente angular é o número que multiplica o x, portanto, = 1.

Como s é perpendicular a reta r, consideramos a condição de perpendicularismo.

Como s passa pelo ponto (1,4), podemos escrever:

Assim, a equação da reta s na forma geral, perpendicular a reta r, que passa pelo ponto P é:

Para saber mais, leia também Equação da Reta.

Como saber se duas retas são perpendiculares (método prático)

Quando conhecemos as equações gerais de duas retas, podemos verificar se são perpendiculares através dos coeficientes (a, b e c) de x e de y.

Assim, dadas as retas:

r: a_r x + b_r y + c_r = 0 e

s: a_s x + b_s y + c_s = 0

Elas serão perpendiculares se:

Exemplo

Reta r: -2x + y + 2 = 0

Reta s: x + 2y - 3 = 0

-2.1 + 1.2 = 0

Portanto, r⊥s (A reta r é perpendicular a reta s).

Equação de uma Reta Perpendicular

A equação geral de uma reta é dada por:

y = mx + b

Se conhecemos uma reta com coeficiente angular m1, a equação de uma reta perpendicular a ela terá o coeficiente angular .

Passos para encontrar a equação de uma reta perpendicular:

1. Identifique o coeficiente angular (m1) da reta original;
2. Calcule o coeficiente angular da reta perpendicular;
3. Substitua m2 e o ponto dado na fórmula y = mx + b para encontrar a equação.

Exemplo
Determine a equação da reta s que passa pelo ponto (1, 2) e é perpendicular a reta r de equação: y = 3x + 2.

Resolução
Passo 1: determinar o coeficiente angular da reta s.

Como ms x mr = -1, temos:

O coeficiente angular da reta r é o 3 (número que multiplica o x).

Passo 2: substituir os valores de x e y (1, 2) na equação geral da reta s.

A equação geral é y = mx + b. Substituindo os valores:

Conclusão
A equação da reta s é .

Qual a diferença entre retas perpendiculares, concorrentes e paralelas

As retas concorrentes são três ou mais linhas que passam pelo mesmo ponto. Imagine várias estradas que se encontram num único cruzamento. Por exemplo, dentro de um triângulo, as linhas que ligam cada canto (vértice) até o meio do lado oposto (chamadas medianas) sempre se encontram em um ponto no meio, chamado de baricentro.

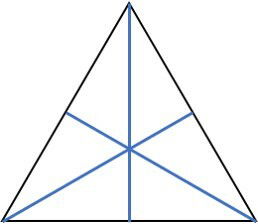
As perpendiculares são um caso especial de concorrência. Retas perpendiculares se cruzam formando quatro ângulos retos (90º).

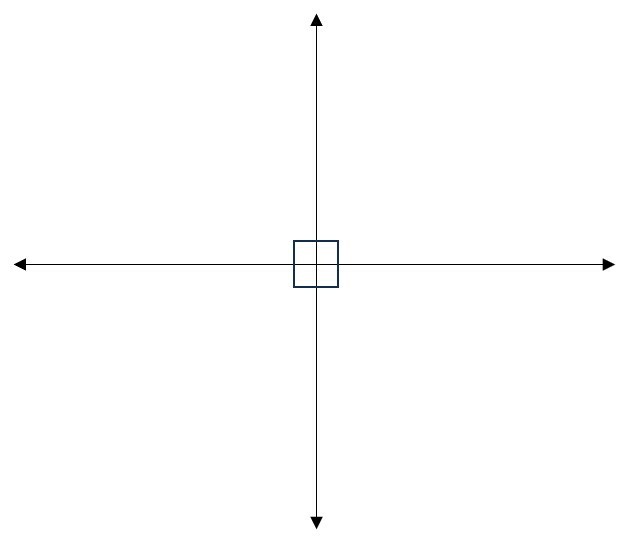
Já as linhas paralelas nunca se cruzam, não importa o quanto sejam prolongadas. Pense em linhas de uma folha de caderno: elas estão sempre separadas, na mesma distância uma das outras.

Na geometria analítica, linhas paralelas têm exatamente a mesma inclinação (mesmo valor de "m"). O que muda nelas é apenas o ponto onde cruzam o eixo Y (chamado intercepto).

Exercícios sobre retas perpendiculares

Questão 1

São dados os pontos A(3,4) e B(1,2). Determine a equação da mediatriz de .

Questão 2

Determine a equação da reta s, perpendicular a reta r de equação 3x + 2y - 4 = 0, no ponto em que esta intersecta o eixo das abscissas.

Demonstração e dedução da condição de perpendicularidade

Para chegar a essa condição, consideramos que a inclinação das retas r e s são respectivamente , conforme a figura abaixo:

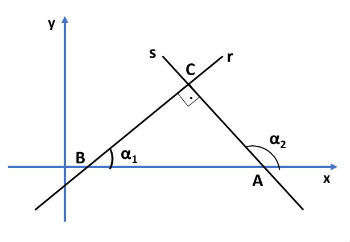
No triângulo ABC da figura identificamos a seguinte relação:

Calculando a tangente dos dois lados da equação, temos:

Lembrando que a tangente de um ângulo é dada pela razão entre o seno e o cosseno deste ângulo, então:

Usando as relações de soma de arcos:

Sendo sen 90º = 1 e cos 90º = 0 e substituindo esses valores na equação acima, encontramos:

Considerando

e que

temos:

Conforme queríamos demonstrar.

Para saber mais, leia também:

• Mediatriz
• Retas
• Retas Paralelas
• Retas Concorrentes
• Geometria analítica

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.