Retas: o que são, classificação, equações e propriedades
Na matemática, as retas são linhas infinitas formadas por pontos. Elas são representadas por letras minúsculas e devem ser desenhadas com setas para os dois lados, indicando que não possuem fim. Já os pontos da reta são indicados por letras maiúsculas.
Note que as retas podem ser utilizadas tanto na geometria plana quanto na geometria espacial. Nesse caso, são chamadas respectivamente de retas no plano e retas no espaço.
Atenção!
As retas diferem das linhas, visto que elas não fazem curva.
Propriedades das Retas
- As retas são linhas infinitas
- As retas possuem somente uma dimensão (unidimensional)
- Numa reta existem infinitos pontos
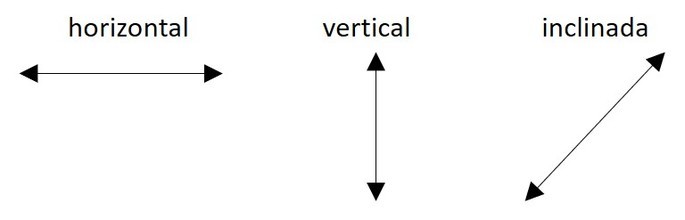
- As retas podem estar em três posições: horizontal, vertical e inclinada
Posição das Retas
As retas podem estar na horizontal, vertical ou inclinada.
Tipos de Retas
Duas ou mais retas possuem posições relativas entre si, podendo estar em planos diferentes ou, no mesmo plano (coplanares).
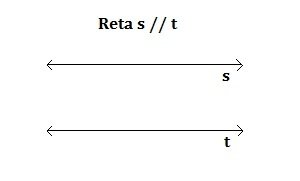
Retas Paralelas: não existe ponto em comum entre as retas, ou seja, elas estão posicionadas uma ao lado da outra e sempre na mesma direção (vertical, horizontal ou inclinada).
Veja também Retas Paralelas
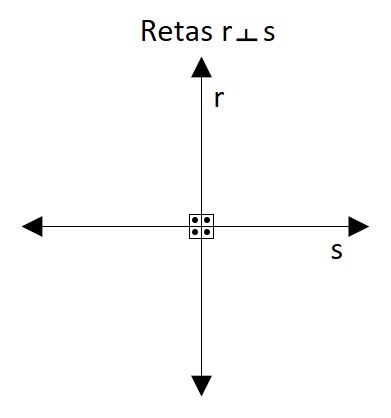
Retas Perpendiculares: possuem um ponto em comum. A intersecção forma quatro ângulos retos (90°) no plano.
Veja também: Retas Perpendiculares
Retas Transversais: São definidas como retas que possuem intersecção com as outras, em pontos diferentes.
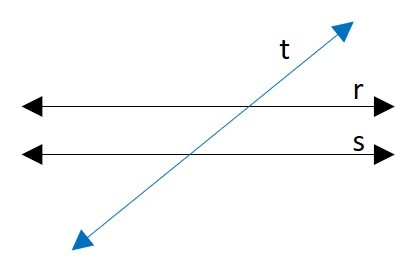
Retas Coincidentes: as retas coincidentes possuem todos os pontos em comum, diferente das retas perpendiculares.

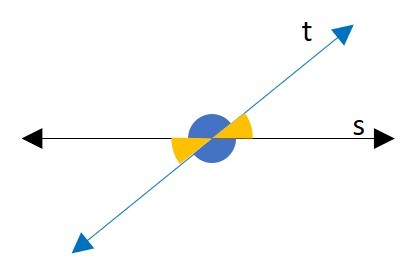
Retas Concorrentes: são duas retas que se encontram em único ponto (vértice). Formando quatro ângulos diferentes de 90°. Os ângulos opostos pelo vértice são iguais.
Veja também: Retas Concorrentes
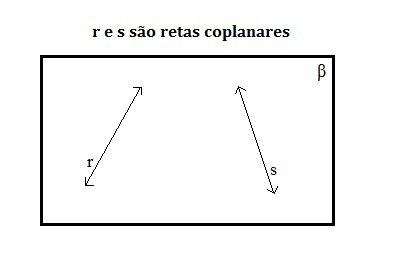
Retas Coplanares: são retas que estão presentes no mesmo plano. Na figura abaixo ambas pertencem ao plano β.
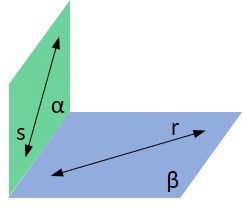
Retas Reversas: são retas que estão presentes em planos distintos, diferentes das retas coplanares.
Equação Geral Da Reta
A Equação Geral da Reta é utilizada quando as retas estão representadas num plano cartesiano. É expressa da seguinte maneira:
Sendo,
a, b e c: números reais constantes
a e b: são valores diferentes de zero (não nulos)
x e y: são as coordenadas de um ponto do plano P (x,y)
Veja também: Equação da Reta
Equação Reduzida da Reta
A Equação Reduzida da Reta também é calculada quando uma reta intercepta o eixo de coordenadas em um ponto do plano cartesiano. Ela é expressa da seguinte maneira:
Sendo,
x e y: coordenadas de um ponto qualquer da reta
m: coeficiente angular da reta
n: coeficiente linear
Reta e Segmento de Reta
A reta é infinita nos dois sentidos, já o segmento de reta é limitado por dois pontos da reta. Ou seja, ele é uma parte da reta que possui início e fim. É representado com um traço acima dos pontos inicial e final da reta.

Veja mais sobre Segmento de Reta.
Reta e Semirreta
As semirretas possuem início, mas não apresentam um fim, ou seja, elas são ilimitadas num dos sentidos. São representadas com uma seta acima das letras, a qual indica a direção da semirreta.

Sendo assim, as semirretas diferem das retas por serem infinitas em apenas um lado e, diferente dos segmentos de retas, pois não são limitadas por dois pontos.
Aprenda mais sobre as semirretas.
Reta Numérica ou Reta Orientada
A reta possui infinitos pontos aos quais a cada um se associa um número real. Em uma reta numérica os números seguem o princípio da sucessão, por isso, estão organizados de forma crescente.
À origem dos números se associa o zero (0) a partir do qual, nos dois sentidos, a reta se prolonga infinitamente.

Os números negativos são representados com valores absolutos decrescentes, com um sinal negativo à frente.
Veja que -1 é menor que 1, pois todo número à esquerda é menor que um número à direita.
-1 < 1
Muitas vezes se convenciona o sentido positivo para direita. Todavia, este sentido é arbitrário e depende da referência adotada.
Pratique exercícios sobre equação da reta resolvidos.
ASTH, Rafael. Retas: o que são, classificação, equações e propriedades. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/retas/. Acesso em:


