Exercícios de Função Afim

Rafael C. Asth
Revisão por Rafael C. Asth
Professor de Matemática e Física

A função afim ou função polinomial do 1º grau, representa qualquer função do tipo f (x) = ax + b, com a e b números reais e a ≠ 0.

Este tipo de função pode ser aplicada em diversas situações do cotidiano, nas mais variadas áreas. Portanto, saber resolver problemas que envolvem este tipo de cálculo é fundamental.

Questão 1

Um atleta ao ser submetido a um determinado treino específico apresenta, ao longo do tempo, ganho de massa muscular. A função P(t) = P0 + 0,19 t, expressa o peso do atleta em função do tempo ao realizar esse treinamento, sendo P0 o seu peso inicial e t o tempo em dias.

Considere um atleta que antes do treinamento apresentava 55 kg e que necessita chegar ao peso de 60 kg, em um mês. Fazendo unicamente esse treinamento, será possível alcançar o resultado esperado?

Resposta correta: Sim.

Substituindo o tempo indicado na função, podemos encontrar o peso do atleta ao final de um mês de treinamento e comparar com o peso que se deseja alcançar.

Vamos então substituir na função o peso inicial (P0) por 55 e o tempo por 30, pois seu valor deve ser dado em dias:

P(30) = 55 + 0,19.30
P(30) = 55 + 0,19.30
P(30) = 55 + 5,7
P(30) = 60,7

Assim, o atleta terá ao final de 30 dias, 60,7 kg. Portanto, usando o treinamento será possível sim atingir a meta.

Questão 2

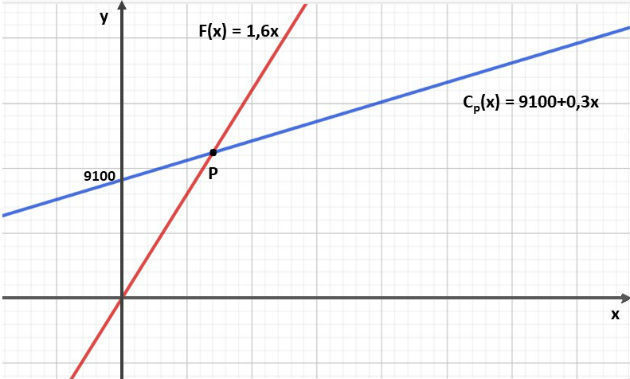
Uma certa indústria produz peças de automóveis. Para produzir essas peças a empresa possui um custo mensal fixo de R$ 9 100,00 e custos variáveis com matéria prima e demais despesas associadas à produção. O valor dos custos variáveis é de R$ 0,30 por cada peça produzida.

Sabendo que o preço de venda de cada peça é de R$ 1,60, determine o número necessário de peças que a indústria deverá produzir por mês para não ter prejuízo.

Resposta correta: pelo menos 7 000 peças por mês.

Para resolver esse problema, vamos considerar como x o número de peças produzidas. Podemos ainda, definir uma função custo de produção Cp(x), que é a soma dos custos fixos e dos custos variáveis.

Essa função é definida por:

Cp (x) = 9 100 + 0,3x

Vamos também estabelecer a função faturamento F(x), que depende do número de peças produzidas.

F(x) = 1,6x

Podemos representar essas duas funções traçando os seus gráficos, conforme mostrado abaixo

Gráfico do lucro da empresa

Observando este gráfico, notamos que existe um ponto de intersecção (ponto P) entre as duas retas. Esse ponto representa o número de peças em que o faturamento é exatamente igual ao custo de produção.

Portanto, para determinar quanto que a empresa precisa produzir para não ter prejuízo, precisamos conhecer esse valor.

Para tal, basta igualar as duas funções definidas:

9100 mais 0 vírgula 3 x igual a 1 vírgula 6 x 1 vírgula 6 x menos 0 vírgula 3 x igual a 9100 1 vírgula 3 x igual a 9100 x igual a numerador 9100 sobre denominador 1 vírgula 3 fim da fração igual a 7000

Assim, será necessário que sejam produzidos pelo menos 7 000 peças por mês, para que a empresa não tenha prejuízo.

Questão 3

Uma empresa de telefonia oferece dois tipos de planos:

  • Plano Plus: 3,5 GB de internet, mais ligações ilimitadas para telefones fixos e celulares.
  • Plano Econômico: 3,5 GB de internet, mais 50 min de ligações para telefones fixos e celulares.

O plano Plus custa por mês R$ 65,90, já o plano Econômico custa R$ 10,80, sendo que é cobrado R$ 1,90 por minuto quando o cliente exceder os 50 min incluídos no plano.

Considerando esses dois planos, usando quantos minutos de ligações por mês, o plano Plus passa a ser mais econômico?

a) 30 min
b) 50 min
c) 60 min
d) 70 min
e) 80 min

Alternativa correta e) 80 min.

O custo mensal do plano Econômico, quando o cliente excede os minutos incluídos no plano, pode ser indicado pela função f(x), sendo x os minutos excedentes. Assim, a função será:

f(x) = 10,8 + 1,9x

Então, para sabermos a partir de quantos minutos mensais vale adquirir o plano Plus, vamos igualar essa função ao valor deste plano:

10 vírgula 8 mais 1 vírgula 9 x igual a 65 vírgula 9 1 vírgula 9 x igual a 65 vírgula 9 menos 10 vírgula 8 1 vírgula 9 x igual a 55 vírgula 1 x igual a numerador 55 vírgula 1 sobre denominador 1 vírgula 9 fim da fração igual a 29

Como é dado uma franquia de 50 min, então para quem gasta por mês 79 min (50+29) os dois planos possuem o mesmo valor. Portanto, usando 80 min, o plano Plus passa a ser mais econômico.

Questão 4

(UERJ - 2014) O reservatório A perde água a uma taxa constante de 10 litros por hora, enquanto o reservatório B ganha água a uma taxa constante de 12 litros por hora. No gráfico, estão representados, no eixo y, os volumes, em litros, da água contida em cada um dos reservatórios, em função do tempo, em horas, representado no eixo x.

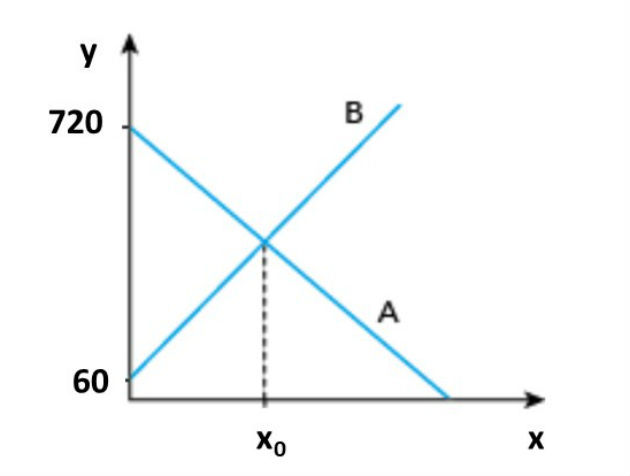
Questão Uerj função afim

Determine o tempo x0, em horas, indicado no gráfico.

Resposta correta: 30 horas.

Como o gráfico das duas funções são retas, as funções são afins. Logo, as funções podem ser escritas na forma f(x) = ax +b.

O coeficiente a de uma função afim representa a taxa de variação e o coeficiente b o ponto em que o gráfico corta o eixo y.

Assim, para o reservatório A, o coeficiente a vale -10, visto que está perdendo água e o valor de b é720. Para o reservatório B, o coeficiente a é igual a 12, pois este reservatório está recebendo água e o valor de b é 60.

Portanto, as retas que representam as funções no gráfico serão:

Reservatório A : y = -10 x + 720
Reservatório B: y = 12 x +60

O valor de x0 será a intersecção das duas retas. Portanto, basta igualar as duas equações para encontrar o seu valor:

12 x mais 60 igual a menos 10 x mais 720 12 x mais 10 x igual a 720 menos 60 22 x igual a 660 x igual a 660 sobre 22 x igual a 30

Logo, o valor de x0 é igual a 30 horas.

Questão 5

(Enem - 2016) Uma cisterna de 6 000 L foi esvaziada em um período de 3h. Na primeira hora foi utilizada apenas uma bomba, mas nas duas horas seguintes, a fim de reduzir o tempo de esvaziamento, outra bomba foi ligada junto com a primeira. O gráfico, formado por dois segmentos de reta, mostra o volume de água presente na cisterna, em função do tempo.

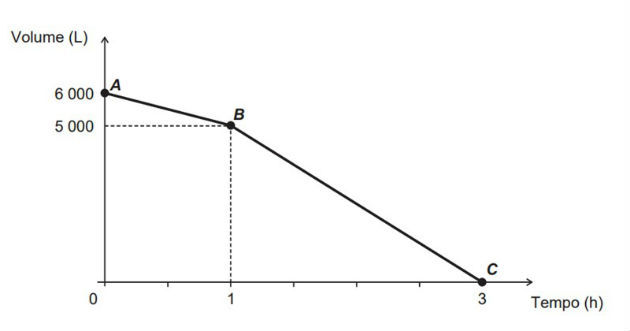
Questão Enem 2016 função afim

Qual é a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora?

a) 1 000
b) 1 250
c) 1 500
d) 2 000
e) 2 500

Alternativa correta: c) 1 500.

A vazão da bomba é igual a taxa de variação da função, ou seja, seu coeficiente angular. Note que na primeira hora, com apenas uma bomba ligada, a taxa de variação era:

y igual a a x mais b 5000 igual a a.1 mais 6000 a igual a numerador 5000 espaço menos 6000 sobre denominador 1 fim da fração igual a menos 1000

Assim, a primeira bomba esvazia a cisterna com um vazão de 1000 l/h.

Ao ligar a segunda bomba, o coeficiente angular muda, e seu valor será:

a igual a numerador 0 menos 5000 sobre denominador 3 menos 1 fim da fração igual a numerador menos 5000 sobre denominador 2 fim da fração igual a menos 2500

Ou seja, as duas bombas ligadas juntas, possuem uma vazão de 2500 l/h.

Para encontrar a vazão da segunda bomba, basta diminuir do valor encontrado a vazão da primeira bomba, então:

2500 - 1000= 1500 l/h

Portanto, a vazão, em litro por hora, da bomba que foi ligada no início da segunda hora é 1500 l/h.

Questão 6

(Cefet - MG - 2015) Um motorista de táxi cobra, para cada corrida, uma taxa fixa de R$ 5,00 e mais R$ 2,00 por quilômetro rodado. O valor total arrecadado (R) num dia é função da quantidade total (x) de quilômetros percorridos e calculado por meio da função R(x) = ax + b, em que a é o preço cobrado por quilômetro e b, a soma de todas as taxas fixas recebidas no dia. Se, em um dia, o taxista realizou 10 corridas e arrecadou R$ 410,00, então a média de quilômetros rodados por corrida, foi de

a) 14
b) 16
c) 18
d) 20

Alternativa correta: c) 18.

Primeiro precisamos escrever a função R(x), e para isso, precisamos identificar os seus coeficientes. O coeficiente a é igual ao valor cobrado pelo quilômetro rodado, ou seja a=2.

Já o coeficiente b é igual a taxa fixa (R$5,00) multiplicada pelo número de corridas, que neste caso, é igual a 10; logo, b será igual a 50 (10.5).

Assim, R(x) = 2x + 50.

Para calcular os quilômetros rodados, temos que encontrar o valor do x. Como R(x) = 410 (total arrecadado no dia), basta substituir esse valor na função:

410 igual a 2 x mais 50 2 x igual a 410 menos 50 2 x igual a 360 x igual a 360 sobre 2 igual a 180

Portanto, o taxista rodou ao final do dia 180 km. Para encontrar a média, basta dividir 180 por 10 (nº de corridas), encontrando então que a média de quilômetros rodados por corrida foi de 18 km.

Questão 7

(Enem - 2012) As curvas de oferta e de demanda de um produto representam, respectivamente, as quantidades que vendedores e consumidores estão dispostos a comercializar em função do preço do produto. Em alguns casos, essas curvas podem ser representadas por retas. Suponha que as quantidades de oferta e de demanda de um produto sejam, respectivamente, representadas pelas equações:

QO = – 20 + 4P
QD = 46 – 2P

em que QO é quantidade de oferta, QD é a quantidade de demanda e P é o preço do produto.

A partir dessas equações, de oferta e de demanda, os economistas encontram o preço de equilíbrio de mercado, ou seja, quando QO e QD se igualam.

Para a situação descrita, qual o valor do preço de equilíbrio?

a) 5
b) 11
c) 13
d) 23
e) 33

Alternativa correta: b) 11.

O valor do preço de equilíbrio é encontrado igualando-se as duas equações dadas. Assim, temos:

menos 20 mais 4 P igual a 46 menos 2 P 4 P mais 2 P igual a 46 mais 20 6 P igual a 66 P igual a 66 sobre 6 igual a 11

Questão 8

(Unicamp - 2016) Considere a função afim f(x) = ax + b definida para todo número real x, onde a e b são números reais. Sabendo que f(4) = 2, podemos afirmar que f(f(3) + f(5)) é igual a

a) 5
b) 4
c) 3
d) 2

Alternativa correta: d) 2.

Sendo a f(4) = 2 e f(4) = 4a + b, então 4a + b = 2. Considerando ainda que f(3) = 3a + b e f(5) = 5a +b, a função da soma das funções será:

f parêntese esquerdo f parêntese esquerdo 3 parêntese direito espaço mais espaço f parêntese esquerdo 5 parêntese direito parêntese direito espaço igual a espaço f parêntese esquerdo espaço 3 a espaço mais espaço b espaço mais 5 a espaço mais b parêntese direito f parêntese esquerdo f parêntese esquerdo 3 parêntese direito espaço mais espaço f parêntese esquerdo 5 parêntese direito parêntese direito espaço igual a espaço f parêntese esquerdo espaço 8 a espaço mais 2 espaço b espaço parêntese direito f parêntese esquerdo f parêntese esquerdo 3 parêntese direito espaço mais espaço f parêntese esquerdo 5 parêntese direito parêntese direito espaço igual a espaço f parêntese esquerdo espaço 2 parêntese esquerdo 4 a mais b parêntese direito parêntese direito f parêntese esquerdo f parêntese esquerdo 3 parêntese direito espaço mais espaço f parêntese esquerdo 5 parêntese direito parêntese direito espaço igual a espaço f parêntese esquerdo espaço 2.2 parêntese direito f parêntese esquerdo f parêntese esquerdo 3 parêntese direito espaço mais espaço f parêntese esquerdo 5 parêntese direito parêntese direito espaço igual a espaço f parêntese esquerdo 4 parêntese direito f parêntese esquerdo f parêntese esquerdo 3 parêntese direito espaço mais espaço f parêntese esquerdo 5 parêntese direito parêntese direito espaço igual a espaço 2

Portanto, sabendo que f(4) = 2, podemos afirmar que f(f(3) + f(5)) é igual a 2.

Questão 9

(Enem 2021) Por muitos anos, o Brasil tem figurado no cenário mundial entre os maiores produtores e exportadores de soja. Entre os anos de 2010 e 2014, houve uma forte tendência de aumento da produtividade, porém, um aspecto dificultou esse avanço: o alto custo do imposto ao produtor associado ao baixo preço de venda do produto. Em média, um produtor gastava R$ 1 200,00 por hectare plantado, e vendia por R$ 50,00 cada saca de 60 kg. Ciente desses valores, um produtor pode, em certo ano, determinar uma relação do lucro L que obteve em função das sacas de 60 kg vendidas. Suponha que ele plantou 10 hectares de soja em sua propriedade, na qual colheu x sacas de 60 kg e todas as sacas foram vendidas.

Qual é a expressão que determinou o lucro L em função de x obtido por esse produtor nesse ano?

a) L(x) = 50x – 1 200
b) L(x) = 50x – 12 000
c) L(x) = 50x + 12 000
d) L(x) = 500x – 1 200
e) L(x) = 1 200x – 500

Resposta: b) L(x) = 50x – 12 000

O lucro é a receita menos o custo.

A receita é o quanto se arrecada. Como cada uma saca, nomeada como x, tem o preço de R$50,00, temos a receito como:

50x

O custo depende é de 1200 por hectare, como são 10 hectares:

10 . 1200 = 12 000

A função fica:

L(x) = 5x - 1200

Questão 10

(Enem 2018) Uma indústria automobilística está testando um novo modelo de carro. Cinquenta litros de combustível são colocados no tanque desse carro, que é dirigido em uma pista de testes até que todo o combustível tenha sido consumido. O segmento de reta no gráfico mostra o resultado desse teste, no qual a quantidade de combustível no tanque é indicada no eixo y (vertical), e a distância percorrida pelo automóvel é indicada no eixo x (horizontal).

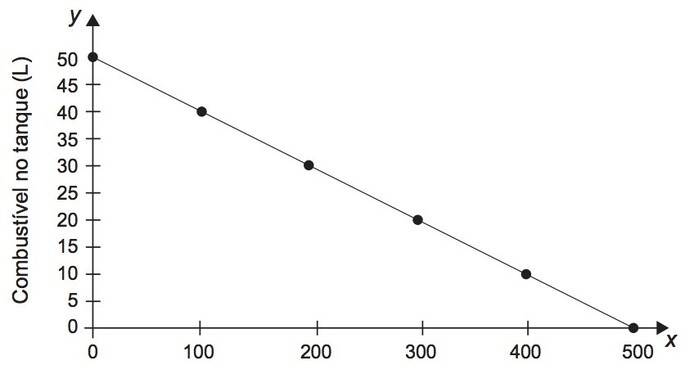
Imagem associada a questão.

A expressão algébrica que relaciona a quantidade de combustível no tanque e a distância percorrida pelo automóvel é

a) reto y espaço igual a espaço menos 10 reto x espaço mais espaço 500

b) reto y igual a numerador menos reto x sobre denominador 10 fim da fração mais 50

c) reto y igual a numerador menos reto x sobre denominador 10 fim da fração mais 500

d) reto y igual a reto x sobre 10 mais 50

e) reto y igual a reto x sobre 10 mais 500

Resposta: b) reto y igual a numerador menos reto x sobre denominador 10 fim da fração mais 50

Como o gráfico é uma reta, trata-se de uma função afim, do tipo:

reto y igual a ax mais reto b

Onde b é o coeficiente linear. Ele representa o valor inicial e pode ser obtido fazendo x = 0.

reto y igual a ax mais reto b reto y igual a reto a.0 mais reto b reto y igual a reto b

Do gráfico, obtemos b = 50.

Como a função é decrescente, a deve ser negativo. O parâmetro a é o coeficiente angular, obtido como:

a = a igual a menos 50 sobre 500 igual a menos 1 sobre 10

Desta forma, a função fica:

reto y igual a numerador menos reto x sobre denominador 10 fim da fração mais 50

Mais exercícios em:

Para saber mais, veja também:

Rafael C. Asth
Revisão por Rafael C. Asth
Professor de Matemática, licenciado e pós-graduado em ensino da Matemática e da Física. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também