Função Afim (Função do 1º Grau)

A função afim, também chamada de função do 1º grau, é uma função definida por:

Sendo a e b números reais.

Neste tipo de função, o número a é chamado de coeficiente de x e representa a taxa de crescimento ou taxa de variação da função. O "a" determina a inclinação da reta.

Já o número b é chamado de coeficiente linear, sendo um termo constante. Ele representa o ponto de intersecção da reta com o eixo y das ordenadas.

A função afim é representada graficamente por uma reta no plano cartesiano.

Exemplos de função afim:

f(x) = x + 5, (com a = 1 e b = 5);

g(x) = 3√3x - 8, (com a =3√3 e b = -8);

h(x) = 1/2x, (com a =1/2 e b = 0);

Toda função afim possui como conjunto domínio os números reais, assim como seu contradomínio, f : ℝ→ℝ. Ainda, nas funções afins, o conjunto imagem é igual ao contradomínio.

Gráfico de uma Função do 1º grau

O gráfico de uma função polinomial do 1º grau é uma reta oblíqua aos eixos Ox e Oy. Desta forma, para construirmos seu gráfico basta encontrarmos pontos que satisfaçam a função.

Exemplo de como desenhar o gráfico de uma função afim:

Construa o gráfico da função f (x) = 2x + 3.

Resolução:

Para construir o gráfico desta função, vamos atribuir valores arbitrários para x, substituir na equação e calcular o valor correspondente para a f (x).

Sendo assim, iremos calcular a função para os valores de x iguais a: - 2, - 1, 0, 1 e 2. Substituindo esses valores na função, temos:

x	2x + 3	f(x)
-2	2 . (-2) + 3	-1
-1	2 . (- 1) + 3	1
0	2 . 0 + 3	3
1	2 . 1 + 3	5
2	2 . 2 + 3	7

Os pontos escolhidos e o gráfico da f (x) são apresentados na imagem abaixo:

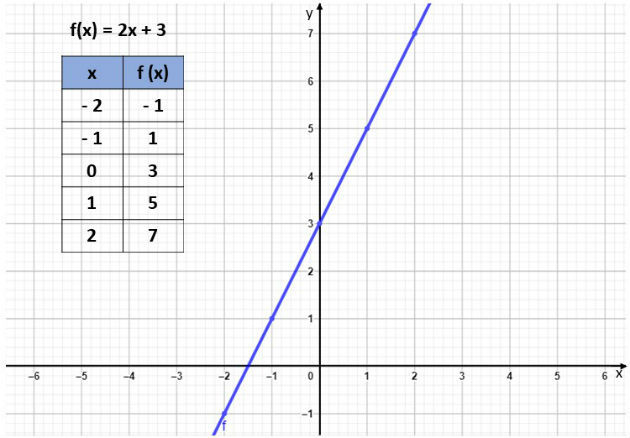
No exemplo, utilizamos vários pontos para construir o gráfico, entretanto, para definir uma reta bastam dois pontos.

Para facilitar os cálculos podemos, por exemplo, escolher os pontos (0,y) e (x,0). Nestes pontos, a reta da função corta o eixo Ox e Oy respectivamente.

Coeficiente Linear e Angular

Como o gráfico de uma função afim é uma reta, o coeficiente a de x é também designado por coeficiente angular. Esse valor representa a inclinação da reta em relação ao eixo Ox.

O termo constante b é chamado de coeficiente linear e representa o ponto onde a reta corta o eixo Oy. Pois sendo x = 0, temos:

y = a.0 + b ⇒ y = b

Quando uma função afim apresentar o coeficiente angular igual a zero (a = 0) a função será chamada de constante. Neste caso, o seu gráfico será uma reta paralela ao eixo Ox.

Abaixo representamos o gráfico da função constante f (x) = 4:

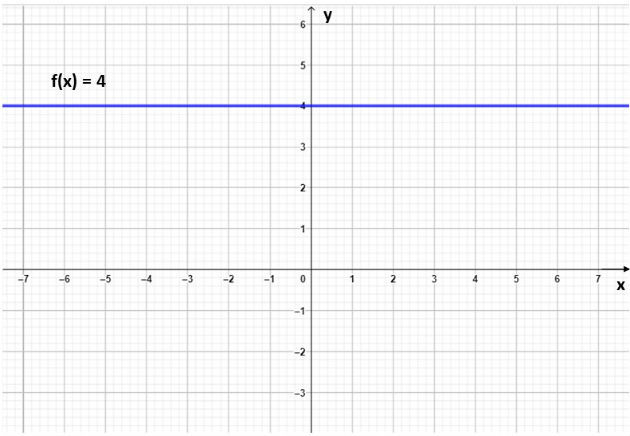
Ao passo que, quando b = 0 e a = 1 a função é chamada de função identidade. O gráfico da função f (x) = x (função identidade) é uma reta que passa pela origem (0,0).

Além disso, essa reta é bissetriz do 1º e 3º quadrantes, ou seja, divide os quadrantes em dois ângulos iguais, conforme indicado na imagem abaixo:

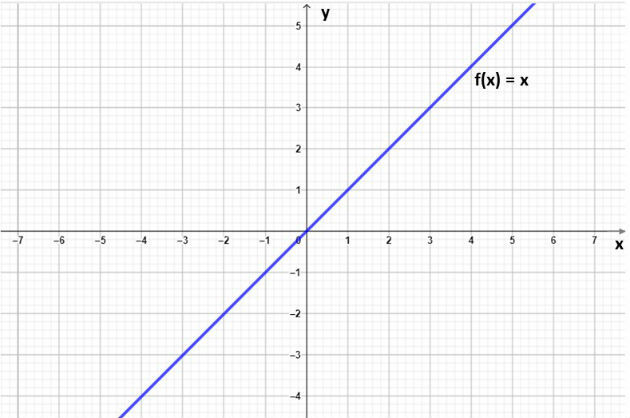
Temos ainda que, quando o coeficiente linear é igual a zero (b = 0), a função afim é chamada de função linear. Por exemplo, as funções f (x) = 2x e g (x) = - 3x são funções lineares.

O gráfico das funções lineares são retas inclinadas que passam pela origem (0,0).

Representamos abaixo o gráfico da função linear f (x) = - 3x:

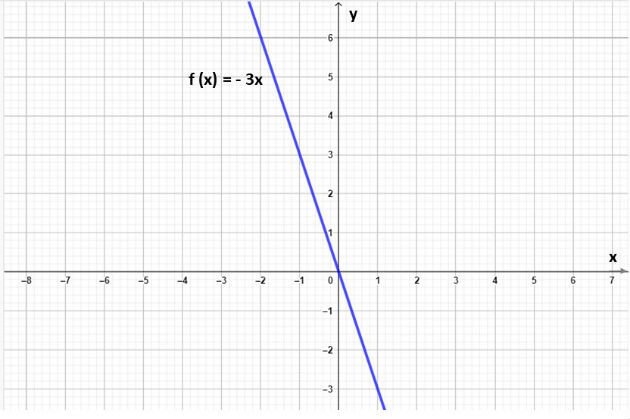
Função Crescente e Decrescente

A função Afim é crescente quando o coeficiente angular for positivo, ou seja, a é maior que zero. Caso contrário, se a for negativo, a função será decrescente.

Por exemplo, a função 2x - 4 é crescente, pois a = 2 (valor positivo). Entretanto, a função - 2x + - 4 é decrescente visto que a = - 2 (negativo). Essas funções estão representadas nos gráficos abaixo:

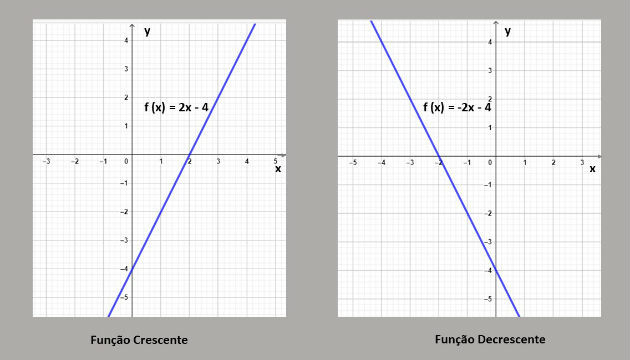
Uma função é crescente quando ao atribuirmos valores cada vez maiores para x, o resultado da f (x) será também cada vez maior.

Já a função decrescente é aquela que ao atribuirmos valores cada vez maiores para x, o resultado da f (x) será cada vez menor.

Leia também sobre o que é função?

Exercícios de função afim

Exercício 1

Em uma determinada cidade, a tarifa cobrada pelos taxistas corresponde a uma parcela fixa chamada de bandeirada e uma parcela referente aos quilômetros rodados. Sabendo que uma pessoa pretende fazer uma viagem de 7 km em que o preço da bandeirada é igual a R$ 4,50 e o custo por quilômetro rodado é igual a R$ 2,75, determine:

a) uma fórmula que expresse o valor da tarifa cobrada em função dos quilômetros rodados para essa cidade.
b) quanto irá pagar a pessoa referida no enunciado.

Quer fazer mais exercícios de função afim? Então não deixe de acessar Exercícios de Função Afim.

Exercício 2

O dono de uma loja de moda praia teve uma despesa de R$ 950,00 na compra de um novo modelo de biquíni. Ele pretende vender cada peça deste biquíni por R$ 50,00. A partir de quantas peças vendidas ele passará a ter lucro?

Para saber mais, leia também:

• Equação do Primeiro Grau
• Equação do 1º Grau - Exercícios
• Função Quadrática
• Função Quadrática - Exercícios
• Função Exponencial
• Função Modular
• Função Injetora
• Função Bijetora
• Função Sobrejetora
• Função Polinomial
• Fórmulas de Matemática