Função Injetora

Rafael C. Asth

Professor de Matemática e Física

A função injetora, também chamada injetiva, é um tipo de função que relaciona cada elemento do domínio a correspondentes distintos no contradomínio.

Assim, dada uma função f (f: A → B), todos os elementos do domínio A têm como imagem elementos distintos no contradomío B. Desta forma, não há dois elementos distintos de A com a mesma imagem em B.

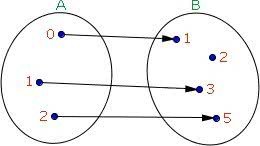
Exemplo

A função é injetora, pois para diferentes x, haverão diferentes y.

Além da função injetora, temos:

Função Sobrejetora: todo elemento do contradomínio B de uma função sobrejetora, é imagem de pelo menos um elemento do domínio A. Em outras palavras, não "sobram" elementos no contradomínio. Isso significa que a imagem e o contradominio são iguais.

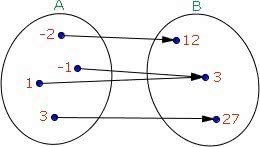
Função Bijetora: é uma função injetora e sobrejetora, onde todos os elementos do domínio, são transformados em elementos distintos no contradomínio.

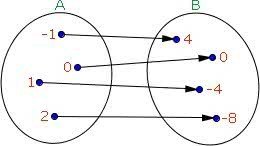
Exemplo

Dada funções: f de A = {0, 1, 2, 3} em B = {1, 3, 5, 7, 9} definida pela lei f(x) = 2x + 1. No diagrama temos:

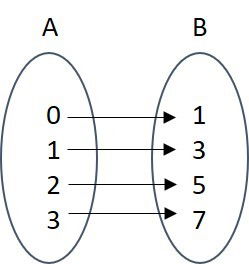
Observe que todos os elementos do domínio A possuem correspondentes distintos em B.

Gráfico de uma função injetora

Os gráficos das funções injetoras podem ser cortados por retas horizontais em apenas um ponto. Ainda que se tracem infinitas retas horizontais, paralelas ao eixo x, cada uma destas retas irá interceptar o gráfico em apenas um ponto.

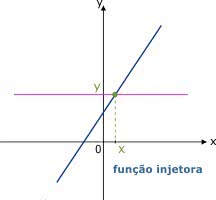
Isto se deve ao fato de que para cada x do domínio só há um y no contradomínio.

Leia também sobre o que é função?

• Domínio, contradomínio e imagem
• Função par e função ímpar

Exercícios de função injetora com gabarito

Exercício 1

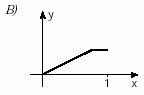
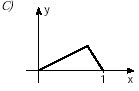
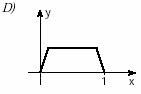
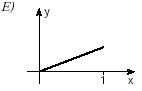
(Unifesp) Há funções y = f(x) que possuem a seguinte propriedade: “a valores distintos de x correspondem valores distintos de y”. Tais funções são chamadas injetoras. Qual, dentre as funções cujos gráficos aparecem abaixo, é injetora?

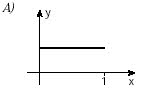
Exercício 2

(IME-RJ) Considera os conjuntos A = {(1,2), (1,3), (2,3)} e B = {1, 2, 3, 4, 5}, e seja a função f: A → B tal que f (x,y) = x + y.

É possível afirmar que f é uma função:

a) injetora.
b) sobrejetora.
c) bijetora.
d) par.
e) ímpar.

Exercício 3

(UFPE) Seja A um conjunto com 3 elementos e B um conjunto com 5 elementos. Quantas funções injetoras de A em B existem?

Pratique também exercícios sobre domínio, contradomínio e imagem.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.