Função Sobrejetora

Rafael C. Asth

Professor de Matemática e Física

A função sobrejetora, também chamada sobrejetiva, é um tipo de função matemática que relaciona todos os elementos do domínio, a todos os elementos do contradomínio. Assim, nas funções sobrejetoras, contradomínio e imagem são iguais.

CD(f) = Im(f)

Na função sobrejetora, todo elemento do contradomínio, é imagem de pelo menos um elemento do domínio. Desta forma, em uma função sobrejetora, é possível que mais de um elemento do domínio, seja transformado pela função em uma mesma imagem.

f: A → B, ocorre a Im(f) = B

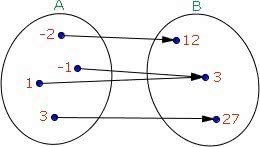
No diagrama acima temos que o domínio dessa função sobrejetora reúne os elementos {-2, -1, 1, 3}. Já o contradomínio é o conjunto representado por {12, 3, 27} e o conjunto imagem é {12, 3, 27}.

Outra característica das sobrejetoras é que não há elementos "sobrando" no contradomínio.

Além da função sobrejetora, há mais dois tipos:

Função Injetora: trata-se de uma função onde todos os elementos do domínio possuem como imagem, elementos distintos no contradomínio.

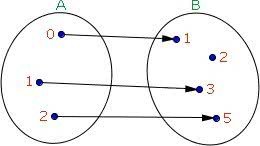
Função Bijetora: corresponde a uma função injetora e sobrejetora, em simultâneo. Dessa forma, todos os elementos do domínio são transformados em elementos distintos no contradomínio.

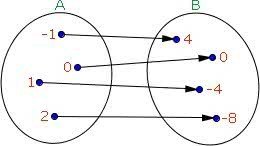
Gráfico da Função Sobrejetora

No gráfico de uma função sobrejetora todos os elementos do contradomínio são também imagem. Desta forma é possível classificar se uma função é ou não sobrejetora de forma prática, verificando se não há "sobras" eu seu contradomínio.

Método gráfico para verificar se uma função é sobrejetora.

1º. Verifica-se o contradomínio da função.
2º. Verifica-se se imagem e contradomínio são iguais.

Exemplo de gráfico de função sobrejetora:

$f parêntese esquerdo x parêntese direito igual a x espaço mais espaço 2 vírgula espaço espaço s e n d o espaço f dois pontos reto números reais seta para a direita reto números reais$

Assim, verificamos que o domínio e o contradomínio estão definidos no conjunto dos números reais.

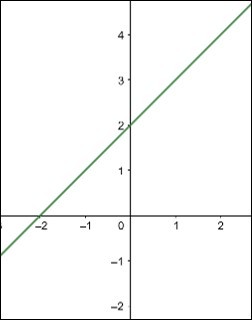
Como não há descontinuidades na função e o domínio e o contradomínio se estendem por toda reta real, a imagem será sempre igual ao contradomínio, ou seja:

CD(f) = Im(f) = R

Exemplo de gráfico de função não sobrejetora:

$f parêntese esquerdo x parêntese direito igual a x ao quadrado menos 2 vírgula espaço s e n d o espaço f dois pontos reto números reais seta para a direita reto números reais$

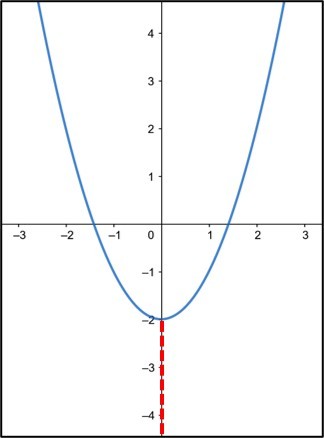
A linha pontilhada mostra uma parte do contradomínio que não é imagem da função. Percebe-se que -3 faz parte do contradomínio, mas não faz parte da imagem.

Assim, $C D parêntese esquerdo f parêntese direito não igual I m parêntese esquerdo f parêntese direito$ .

Exercícios de função sobrejetora com gabarito

Exercício 1

(UFMG-MG) Seja f a função de IR em IR, dada pelo gráfico a seguir. É correto afirmar que:

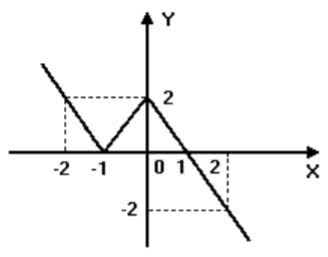
a) f é sobrejetora e não injetora.
b) f é bijetora.
c) f(x) = f(-x) para todo x real.
d) f(x) > 0 para todo x real.
e) o conjunto imagem de f é ] - ∞; 2 ]

Ver Resposta

Resposta correta: a) f é sobrejetora e não injetora.

É sobrejetora pois para todo contradomínio IR há uma correspondente imagem. Ou seja, para todo $x pertence reto números reais$ no domínio, há um $y espaço pertence I R$ na imagem.

A função não é injetora, pois para dois pontos do domínio, há uma única imagem. Por exemplo, os pontos -2 e 0, têm como imagem o 2.

Exercício 2

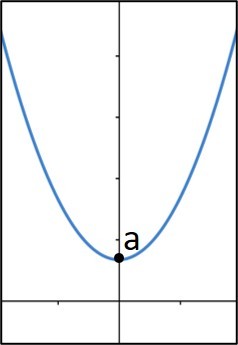
(UFT) Seja a um número real e f : ]–∞, ∞[→[a , ∞[ uma função definida por f(x) = m²x² + 4mx + 1, com m ≠ 0. O valor de a para que a função f seja sobrejetora é:

a) –4
b) –3
c) 3
d) 0
e) 2

Ver Resposta

Resposta correta: b) –3

O domínio da função é a própria reta real, que vai de menos infinito a mais infinito. ]–∞, ∞[
O contradomínio da função vai de a, até mais infinito. [a , ∞[

Para a função ser sobrejetora, a imagem deve ser igual ao contradomínio, ou seja, Im(f) = [a , ∞[

Lembre-se que a imagem e o contradomínio estão no eixo y.

A lei de formação da função é um polinômio do segundo grau, portanto, seu gráfico é uma parábola.

$f parêntese esquerdo x parêntese direito igual a m ao quadrado x ao quadrado espaço mais espaço 4 m x espaço mais espaço 1 vírgula espaço c o m espaço m espaço não igual espaço 0$

Um gráfico de uma função do segundo grau é do tipo:

Na lei de formação da função se o termo que acompanha o x² for positivo, a concavidade é voltada para cima. Como m está elevado ao quadrado, esta parâmetro sempre será positivo.

A imagem da função será de a, ponto de ordenada que marca o vértice da função, até o infinito, se igualando com o contradomínio.

Sendo assim, devemos determinar o a ordenada y do vértice. Uma das maneiras de calcular é:

$y com v subscrito igual a menos numerador incremento sobre denominador 4 a fim da fração$

onde $incremento igual a b ao quadrado menos 4. a. c$

Os parâmetros são:

a = m²
b = 4m
c=1

Substituindo temos:

$y com v subscrito igual a menos numerador incremento sobre denominador 4 a fim da fração igual a menos numerador b ao quadrado menos 4. a. c sobre denominador 4 a fim da fração y com v subscrito igual a menos numerador abre parênteses 4 m fecha parênteses ao quadrado menos 4. m ao quadrado.1 sobre denominador 4 m ao quadrado fim da fração y com v subscrito igual a menos numerador 16 m ao quadrado menos 4 m ao quadrado sobre denominador 4 m ao quadrado fim da fração y com v subscrito igual a menos numerador 12 riscado diagonal para cima sobre m ao quadrado fim do riscado sobre denominador 4 riscado diagonal para cima sobre m ao quadrado fim do riscado fim da fração y com v subscrito igual a menos 12 sobre 4 y com v subscrito igual a menos 3$

Assim, para a função ser sobrejetora o valor de a deve ser igual a -3.

Conheça

Pratique também exercícios sobre domínio, contradomínio e imagem.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações