Função Logarítmica (o que é, propriedades e exercícios)

Revisão por Rafael C. Asth

Professor de Matemática e Física

PA função logarítmica de base a é definida como f (x) = log_a x, com a real, positivo e a ≠ 1. A função inversa da função logarítmica é a função exponencial.

O logaritmo de um número é definido como o expoente ao qual se deve elevar a base a para obter o número x, ou seja:

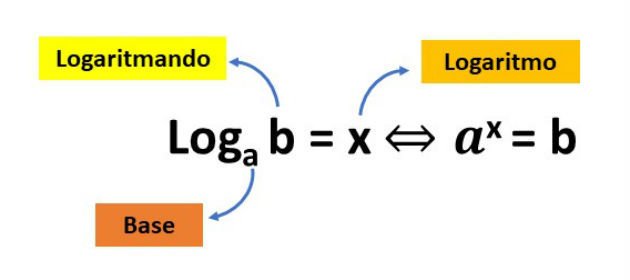
Exemplos de funções logarítmicas:

Domínio da função logarítmica

O domínio de uma função representa os valores de x onde a função é definida. No caso da função logarítmica, devemos considerar as condições de existência do logaritmo.

Portanto, o logaritmando deve ser positivo e a base também deve ser positiva e diferente de 1.

Exemplo: Determine o domínio da função f (x) = log₂ (x + 3).

Resolução:

Para encontrar o domínio, devemos considerar que (x + 3) > 0, pela condição de existência do logaritmo. Resolvendo essa inequação, temos:

x + 3 > 0
x > - 3

Assim, o domínio da função pode ser representado por:

Conclusão:

O conjunto domínio da função f (x) = log₂ (x + 3), são todos os números reais maiores do que -3.

Você pode se interessar por relembrar logaritmo.

Gráfico da função logarítmica

De uma forma geral, o gráfico da função y = log_a x está localizado no I e IV quadrantes, pois a função só é definida para x > 0.

Além disso, a curva da função logarítmica não toca o eixo y e corta o eixo x no ponto de abscissa igual a 1, pois:

Quando y = 0, temos:

Aplicando a definição de logaritmo:

Para qualquer valor de a, x deve ser 1.

Abaixo, apresentamos o esboço do gráfico da função logarítmica.

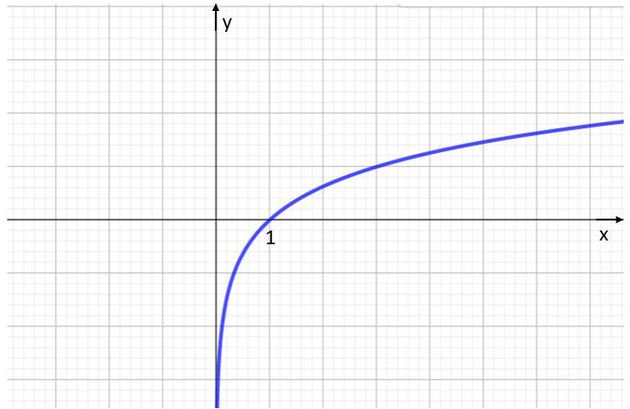
Função crescente e decrescente

Uma função logarítmica será crescente quando a base a for maior que 1, ou seja, x₁ < x₂ ⇔ log_a x₁ < log_a x₂. Por exemplo, a função f (x) = log₂ x é uma função crescente, pois a base é igual a 2.

Para verificar que essa função é crescente, atribuímos valores para x na função e calculamos a sua imagem. Os valores encontrados estão na tabela abaixo.

Observando a tabela, notamos que quando o valor de x aumenta, a sua imagem também aumenta. Abaixo, representamos o gráfico desta função.

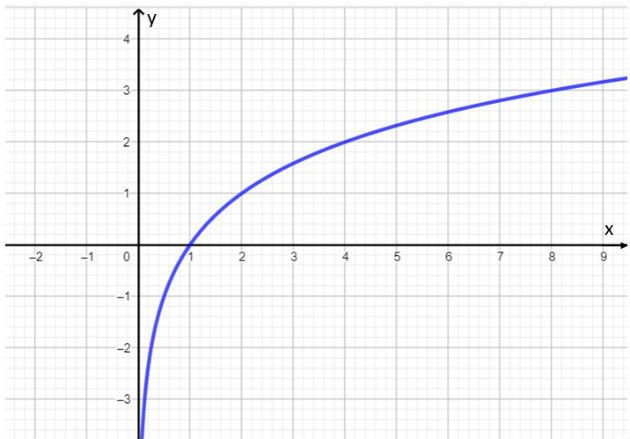
Por sua vez, as funções cujas bases são valores maiores que zero e menores que 1 são decrescentes, ou seja, x₁ < x₂ ⇔ log_a x₁ > log_a x₂. Por exemplo, é uma função decrescente, pois a base é igual a .

Calculamos a imagem de alguns valores de x desta função e o resultado encontra-se na tabela abaixo:

Notamos que, enquanto os valores de x aumentam, os valores das respectivas imagens diminuem. Desta forma, constatamos que a função é uma função decrescente.

Com os valores encontrados na tabela, traçamos o gráfico dessa função. Note que quanto menor o valor de x, mais perto do zero a curva logarítmica fica, sem, contudo, cortar o eixo y.

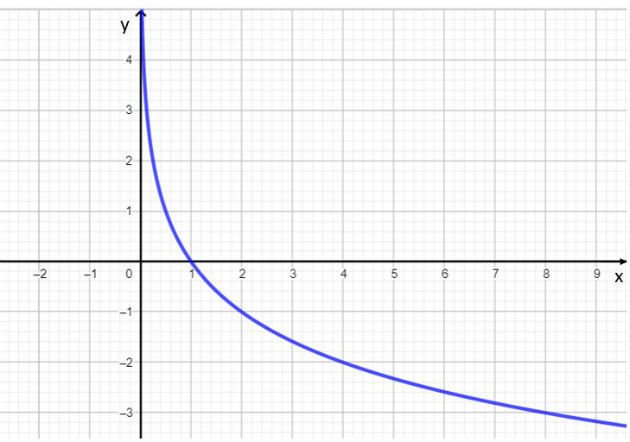
Exercícios sobre função logarítmica

Exercício 1

(PUC/SP - 2018) As funções , com k um número real, se intersectam no ponto . O valor de g(f(11)) é

Exercício 2

(Enem - 2011) A Escala de Magnitude de Momento (abreviada como MMS e denotada como M_w), introduzida em 1979 por Thomas Haks e Hiroo Kanamori, substituiu a Escala de Richter para medir a magnitude dos terremotos em termos de energia liberada. Menos conhecida pelo público, a MMS é, no entanto, a escala usada para estimar as magnitudes de todos os grandes terremotos da atualidade. Assim como a escala Richter, a MMS é uma escala logarítmica. M_w e M_o se relacionam pela fórmula:

Onde M_o é o momento sísmico (usualmente estimado a partir dos registros de movimento da superfície, através dos sismogramas), cuja unidade é o dina·cm.

O terremoto de Kobe, acontecido no dia 17 de janeiro de 1995, foi um dos terremotos que causaram maior impacto no Japão e na comunidade científica internacional. Teve magnitude M_w = 7,3.

Mostrando que é possível determinar a medida por meio de conhecimentos matemáticos, qual foi o momento sísmico M_o do terremoto de Kobe (em dina.cm)

a) 10^{- 5,10}
b) 10^{- 0,73}
c) 10^12,00
d) 10^21,65
e) 10^27,00

Para saber mais, veja também:

• Propriedades dos Logaritmos
• Logaritmo - Exercícios
• O que é função
• Fórmulas de Matemática

Função Exponencial

A inversa da função logarítmica é a função exponencial. A função exponencial é definida como f(x) = a^x, com a real positivo e diferente de 1.

Uma relação importante é que o gráfico de duas funções inversas são simétricos em relação à bissetriz dos quadrantes I e III.

Desta maneira, conhecendo o gráfico da função logarítmica de mesma base, por simetria podemos construir o gráfico da função exponencial.

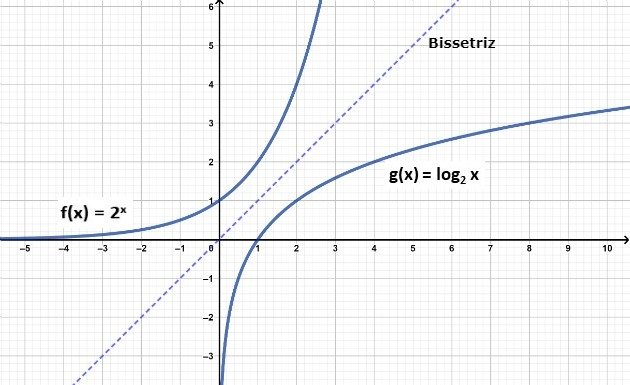
No gráfico acima, observamos que enquanto a função logarítmica cresce lentamente, a função exponencial cresce rapidamente.

• Função exponencial
• Função quadrática
• Função Afim (Função do 1º Grau)

Revisão por Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Edição por Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.