Logaritmo

Rosimar Gouveia

Professora de Matemática e Física

Logaritmo de um número b na base a é igual ao expoente x ao qual se deve elevar a base, de modo que a potência a^x seja igual a b, sendo a e b números reais e positivos e a≠1.

Desta forma, o logaritmo é a uma operação na qual queremos descobrir o expoente que uma dada base deve ter para resultar em uma certa potência.

Por esse motivo, para fazer operações com logaritmos é necessário conhecer as propriedades da potenciação.

Definição de logaritmo

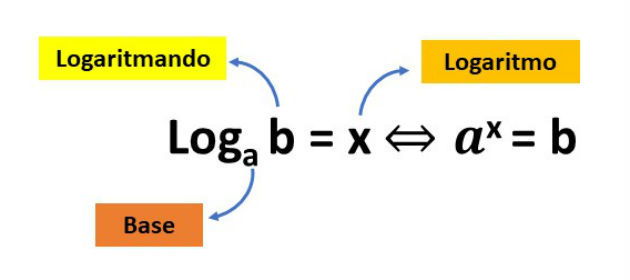
Lê-se logaritmo de b na base a, sendo a > 0 e a ≠ 1 e b > 0.

Quando a base de um logaritmo for omitida, significa que seu valor é igual a 10. Este tipo de logaritmo é chamado de logaritmo decimal.

Como calcular um logaritmo?

O logaritmo é um número e representa um dado expoente. Podemos calcular um logaritmo aplicando diretamente a sua definição.

Exemplo

Qual o valor do log₃ 81?

Solução

Neste exemplo, queremos descobrir qual expoente devemos elevar o 3 para que o resultado seja igual a 81. Usando a definição, temos:

log₃ 81 = x ⇔ 3^x = 81

Para encontrar esse valor, podemos fatorar o número 81, conforme indicado abaixo:

Substituindo o 81 por sua forma fatorada, na equação anterior, temos:

3^x = 3⁴

Como as bases são iguais, chegamos a conclusão que x = 4.

Consequência da definição dos logaritmos

• O logaritmo de qualquer base, cujo logaritmando seja igual a 1, o resultado será igual a 0, ou seja, log_a 1 = 0. Por exemplo, log₉ 1 = 0, pois 9⁰ =1.
• Quando o logaritmando é igual a base, o logaritmo será igual a 1, assim, log_a a = 1. Por exemplo, log₅ 5 = 1, pois 5¹= 5
• Quando o logaritmo de a na base a possui uma potência m, ele será igual ao expoente m, ou seja log_a a^m = m, pois usando a definição a^m = a^m. Por exemplo, log₃ 3⁵ = 5.
• Quando dois logaritmos com a mesma base são iguais, os logaritmandos também serão iguais,ou seja, log_a b = log_a c ⇔ b = c.
• A potência de base a e expoente log_a b será igual a b, ou seja a^log_ab = b.

Propriedades dos Logaritmos

• Logaritmo de um produto: O logaritmo de um produto é igual a soma de seus logaritmos: Log_a (b.c) = Log_a b + log_a c
• Logaritmo de um quociente: O logaritmo de um quociente é igual a diferença dos logaritmos: Log_a = Log_a b - Log_a c
• Logaritmo de uma potência: O logaritmo de uma potência é igual ao produto dessa potência pelo logaritmo: Log_a b^m = m . Log_a b
• Mudança de base: Podemos mudar a base de um logaritmo usando a seguinte relação:

Exemplos

1) Escreva os logaritmos abaixo na forma de um único logaritmo.

a) log₃ 8 + log₃ 10
b) log₂ 30 - log₂ 6
c) 4 log₄ 3

Solução

a) log₃ 8 + log₃ 10 = log₃ 8.10 = log₃ 80
b)
c) 4 log₄ 3 = log₄ 3⁴ = log₄ 81

2) Escreva o log₈ 6 como uma razão de logaritmos na base 2, em seguida, simplifique.

Solução

Cologaritmo

O chamado cologaritmo é um tipo especial de logaritmo expresso pela expressão:

colog_a b = − log_a b

Podemos ainda escrever que:

Para saber mais, veja também:

• Função Logarítmica
• Função Exponencial
• Função Exponencial - Exercícios
• Função Modular

Curiosidades sobre os logaritmos

• O termo logaritmo vem do grego, onde “logos” significa razão e “arithmos” corresponde a número.
• Os criadores dos Logaritmos foram John Napier (1550-1617), matemático escocês, e Henry Briggs (1531-1630), matemático inglês. Eles criaram esse método com o intuito de facilitarem os cálculos mais complexos que ficou conhecido como “logaritmos naturais” ou “logaritmos neperianos”, em alusão a um de seus criadores: John Napier.

Exercícios Resolvidos

1) Sabendo que o , calcule o valor do log₉ 64.

2) UFRGS - 2014

Atribuindo para log 2 o valor 0,3, então os valores de log 0,2 e log 20 são, respectivamente,

a) - 0,7 e 3 .
b) - 0,7 e 1,3.
c) 0,3 e 1,3.
d) 0,7 e 2,3.
e) 0,7 e 3.

Para mais questões de logaritmo, veja Logaritmo - Exercícios.

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.