Função Inversa

Rafael C. Asth

Professor de Matemática e Física

A função inversa é um tipo de função bijetora, ou seja, ela é sobrejetora e injetora em simultâneo.

Recebe esse nome, pois a partir de uma função, é possível inverter os elementos correspondentes, de modo a escrever outra.

Se uma função leva os elementos de seu domínio A ao seu contradomínio B, a função inversa faz o caminho de volta, retornando os elementos de B para A.

Seja a função de domínio A e contradomínio B:

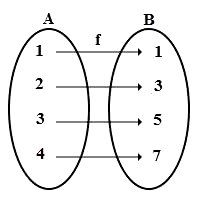
Sua função inversa de domínio B e contradomínio A, é:

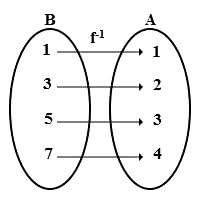
Dada uma função bijetora f: A → B com domínio A e contradomínio B, ela apresenta a função inversa f^-1: B → A, com domínio B e contradomínio A.

Exemplo

Dadas as funções: A = {-2, -1, 0, 1, 2} e B = {-16, -2, 0, 2, 16} observe a imagem abaixo:

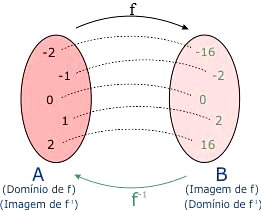
Assim, podemos compreender que o domínio de f corresponde a imagem de f^-1. Já a imagem de f é igual ao domínio de f^-1.

Método para escrever a função inversa

Para escrever a fórmula da função inversa de uma função bijetora, precisamos lembrar que.

1º passo: na função bijetora, substituir f(x) por y;

2º passo: onde tem x troca-se por y e, onde tem y troca-se por x;

3º passo: isola-se o y de um lado da igualdade;

4º passo: reescreve-se a função, substituindo y por .

Exemplo
Escrever a função inversa da função bijetora f(x) = 9x.

1º passo: y = 9x

2º passo: x = 9y

3º passo:

4º passo:

Gráfico da Função Inversa

O gráfico de determinada função e de sua inversa é representado pela simetria em relação à reta y = x.

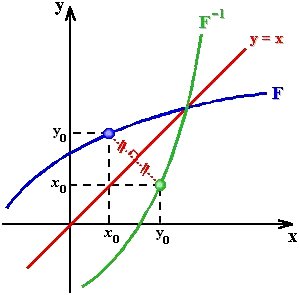
Leia também sobre o que é função?

Exercícios de função inversa

Exercício 1

(FEI) Se a função real f é definida por f(x) = 1 / (x + 1) para todo x > 0, então f^-1(x) é igual a:

a) 1 – x
b) x + 1
c) x ^-1 – 1
d) x ^-1 + 1
e) 1 / (x + 1)

Exercício 2

(UFPA) O gráfico de uma função f(x) = ax + b é uma reta que corta os eixos coordenados nos pontos (2, 0) e (0, -3). O valor de f (f ^-1(0)) é

a) 15/2
b) 0
c) –10/3
d) 10/3
e) –5/2

Veja também:

• Função Modular
• Função composta
• Domínio, contradomínio e imagem
• Função par e função ímpar

Pratique também exercícios sobre domínio, contradomínio e imagem.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.