Função Bijetora

Rafael C. Asth

Professor de Matemática e Física

A função bijetora, também chamada bijetiva, é um tipo de função matemática que relaciona cada elemento do domínio A, a um elemento diferente no contradomínio B. Além disto, todo elemento do contradomínio B é imagem de A.

Desse modo, a função bijetora promove uma correspondência biunívoca, pois os elementos do domínio A possuem correspondentes únicos no contradomínio B. Importante notar que eles apresentam o mesmo número de elementos.

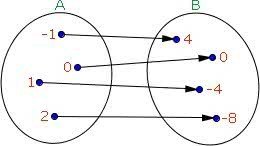
Função Bijetora

A partir desse diagrama, podemos concluir que:

O domínio dessa função é o conjunto A = {-1, 0, 1, 2}. O contradomínio reúne os elementos, B = {4, 0, -4, -8}. Já o conjunto imagem da função é definido por: Im(f) = {4, 0, -4, -8}. A imagem e o contradomínio são iguais.

A função bijetora recebe esse nome, pois ela é injetora e sobrejetora.

Na função injetora, todos os elementos do domínio A têm como imagem elementos distintos no contradomínio B.

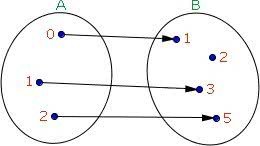
Já na função sobrejetora, todo elemento do contradomínio é imagem de pelo menos um elemento do domínio.

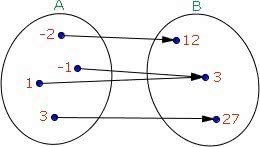
Exemplos de Funções Bijetoras

Dada a função f definida pela lei y = 2x – 1, temos:

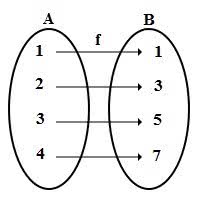
Cada elemento de A, é transformado em um elemento diferente de B. Da mesma forma, cada elemento de B é imagem de apenas um elemento de A, por isto, dizemos ser uma correspondência biunívoca. Ainda, não há elementos sobrando em B, ou seja, o contradomínio B e a imagem da função são iguais.

Função Inversa

Vale notar que a função bijetora sempre admite uma função inversa (f ^-1). Ou seja, é possível inverter e relacionar os elementos de ambas:

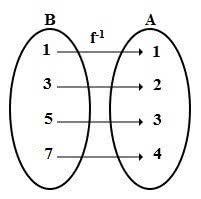
Outros exemplos de funções bijetoras:

f: R → R tal que f(x) = 2x
f: R → R tal que f(x) = x³
f: R₊ → R₊ tal que f(x) = x²
f: R^* → R^* tal que f(x) = 1/x

Gráfico Função Bijetora

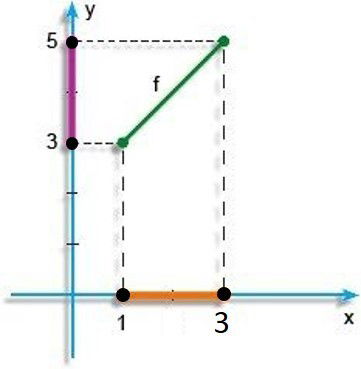
Confira abaixo o gráfico de uma função bijetora f(x) = x + 2, onde f: [1; 3] → [3; 5]:

Exercícios de Função Bijetora

Exercício 1

(Unimontes-MG) Considere as funções f:[0,+∞] ⟶ [0,+ ∞] e g: R⟶R, definidas por f(x) = x² e g(x) = x².

É correto afirmar que

a) g é bijetora.
b) f é bijetora.
c) f é injetora e g é sobrejetora.
d) f é sobrejetora e g é injetora.

Ver Resposta

Resposta correta: b) f é bijetora.

A definição f:[0,+∞] ⟶ [0,+ ∞] é equivalente a f: R+ ⟶ R+.

a) ERRADA:
Se fizermos f(2) = 2² = 4,
Se fizermos f(-2) = (-2)² = 4

Desta forma, dois elementos do domínio levam a um único elemento do contradomínio. Logo a função não é injetora e portanto, não é bijetora.

c) A função f é injetora mas g não é sobrejetora, pois o contradomínio da função está definido em R, mas a x² só pode retornar números positivos. Logo, a imagem e o domínio de g são diferentes, portanto, g não é sobrejetora.

d) A função f é sobrejetora por está definida em R+ ⟶ R+, e x² sempre retorna um número positivo, de modo que Im(f) = CD(f).
No entanto g não é injetora pois, dois elementos do domínio podem levar a um único elemento no contradomínio., como: f(3) = f(-3) = 9.

Exercício 2

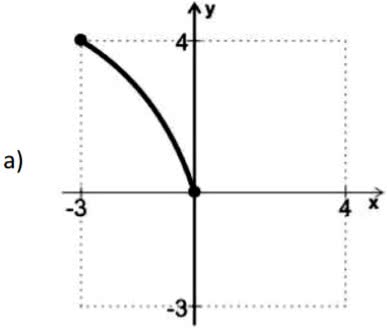
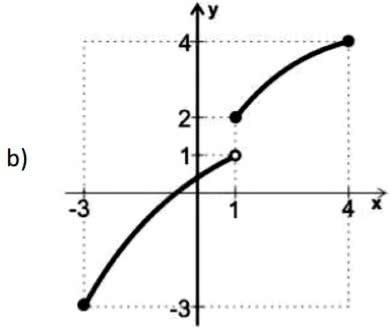
(UFT) Cada um dos gráficos abaixo representa uma função y = f(x) tal que f: Df ⟶ [-3, 4]; Df ⊂ [-3, 4]. Qual deles representa uma função bijetora no seu domínio?

Ver Resposta

Resposta correta: d)

a) ERRADA
O contradomínio da função está definido no intervalo [-3, 4] e a imagem em [0, 4]. Como imagem e contradomínio são diferentes a função não é sobrejetora, logo, não é bijetora.

b) Não é sobrejetora pois a imagem não inclui o intervalo [1, 2), logo não é bijetora.

c) Não é injetora pois, elementos diferentes no domínio levam a mesma imagem, Im(4), na parte em que a função é constante e horizontal. Logo não é bijetora.

d) É injetora pois, cada elemento do domínio leva a um único elemento no contradomínio e é sobrejetora pois, a imagem é igual ao domínio.

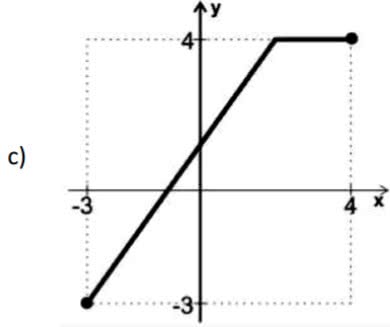
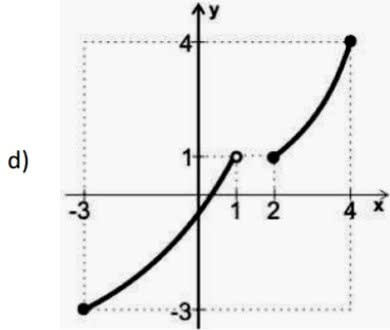
Exercício 3

(UFOP- MG/) Seja f:R → R; f(x) = x³

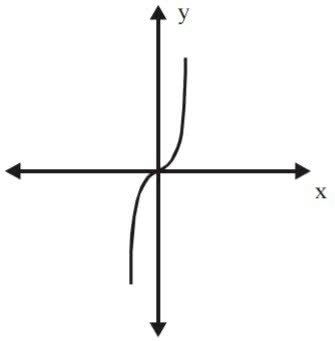
Então podemos afirmar que:

a) f é uma função par e crescente.
b) f é uma função par e bijetora.
c) f é uma função ímpar e decrescente.
d) f é uma função ímpar e bijetora.
e) f é uma função par e decrescente

Ver Resposta

Resposta correta: d) f é uma função ímpar e bijetora.

É bijetora pois é injetora e sobrejetora.

É injetora uma vez que, cada elemento do domínio leva a apenas uma imagem diferente no contradomínio.
É sobrejetora uma vez que, a imagem e igual ao contradomínio.

A função x³ é ímpar, pois:

$f parêntese esquerdo x parêntese direito espaço igual a espaço menos espaço f parêntese esquerdo menos x parêntese direito$

Por exemplo, fazendo x = 2, temos:

$f parêntese esquerdo x parêntese direito espaço igual a espaço 2 ao cubo espaço igual a espaço 8$

$menos espaço f parêntese esquerdo menos x parêntese direito espaço igual a espaço menos espaço parêntese esquerdo menos 2 parêntese direito ao cubo espaço igual a espaço 8$

Veja também

Pratique também exercícios sobre domínio, contradomínio e imagem.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações