Função composta: entenda o que são e como determiná-las

Rafael C. Asth

Professor de Matemática e Física

Uma função composta, também conhecida por função de função, é uma combinação de funções. O nome composta aqui traz justamente a ideia de compor uma nova função a partir de outras.

Considere uma função f(x), com A como sendo seu conjunto domínio, e B como contradomínio (f: A → B). Suponha também uma função g(x) de domínio B e contradomínio C (g: B → C).

A função composta de g com f, representada por gof, será:

$começar estilo tamanho matemático 20px reto g operador anelar reto f espaço igual a espaço reto g parêntese esquerdo reto f parêntese esquerdo reto x parêntese direito parêntese direito fim do estilo$

Perceba que os elementos x na função g(x), agora são os elementos f(x) da função f. Portanto, o domínio da função g é o contradomínio da função f.

A função f leva um elemento x do domínio A a um elemento y contradomínio B.
A função g leva um elemento x do domínio B a um elemento y ao contradomínio C.

A função composta gof liga diretamente um elemento x do conjunto domínio A a um elemento y ao contradomínio C.

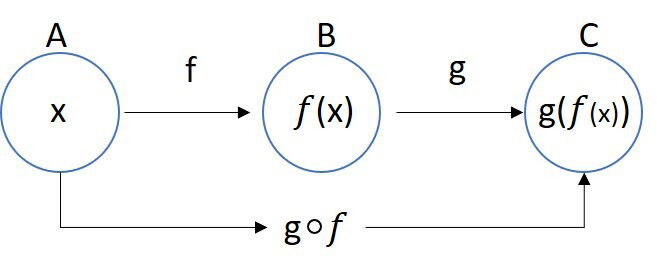
Assim, é válido que:

$gof espaço parêntese esquerdo reto x parêntese direito espaço igual a espaço reto g parêntese esquerdo reto f parêntese esquerdo reto x parêntese direito parêntese direito$

Realizando o caminho inverso e saindo de C para A, temos:

$fog espaço parêntese esquerdo reto x parêntese direito espaço igual a espaço reto f parêntese esquerdo reto g parêntese esquerdo reto x parêntese direito parêntese direito$

Note que nas funções compostas as operações entre as funções não são comutativas. Ou seja, fog ≠ gof.

Como determinar a função composta

Na prática, para determinar uma função composta, aplica-se uma função no domínio da outra, substituindo a variável x pela lei da outra função.

Exemplo
Determine as funções compostas gof(x) e fog(x) das funções:

f(x) = 2x + 2
g(x) = 5x.

Determinando gof (x):
Na função g(x), substituímos a variável x, pela função f(x), da seguinte forma:

$gof parêntese esquerdo reto x parêntese direito espaço igual a espaço reto g parêntese recto esquerdo reto f parêntese esquerdo reto x parêntese direito parêntese recto direito$

$reto g parêntese esquerdo reto x parêntese direito espaço igual a espaço 5 reto x espaço igual a espaço 5. espaço reto f parêntese esquerdo reto x parêntese direito igual a espaço 5 parêntese esquerdo 2 reto x mais 2 parêntese direito espaço igual a espaço 10 reto x espaço mais espaço 10$

Determinando fog (x):
Na função f(x), substituímos a variável x, pela função g(x), da seguinte forma:

$fog parêntese esquerdo reto x parêntese direito espaço igual a espaço reto f parêntese recto esquerdo reto g parêntese esquerdo reto x parêntese direito parêntese recto direito espaço$

$reto f parêntese esquerdo reto x parêntese direito igual a 2 reto x espaço mais espaço 2 igual a espaço 2. reto g parêntese esquerdo reto x parêntese direito espaço mais espaço 2 igual a espaço 2 parêntese esquerdo 5 reto x parêntese direito espaço mais espaço 2 espaço igual a espaço 10 reto x espaço mais espaço 2$

Exercícios de função composta com gabarito

Exercício 1

(Mackenzie) As funções f(x) = 3 – 4x e g(x) = 3x + m são tais que f(g(x)) = g(f(x)), qualquer que seja x real. O valor de m é:

a) 9/4
b) 5/4
c) –6/5
d) 9/5
e) –2/3

Ver Resposta

Alternativa c: –6/5

Resolução

1º passo: determinar as funções compostas

Determinando f(g(x))

$f parêntese esquerdo x parêntese direito espaço igual a espaço 3 espaço menos espaço 4 x f parêntese esquerdo g parêntese esquerdo x parêntese direito parêntese direito espaço igual a espaço 3 espaço menos espaço 4. g parêntese esquerdo x parêntese direito f parêntese esquerdo g parêntese esquerdo x parêntese direito parêntese direito espaço igual a espaço 3 espaço menos espaço 4. parêntese esquerdo 3 x espaço mais espaço m parêntese direito f parêntese esquerdo g parêntese esquerdo x parêntese direito parêntese direito espaço igual a espaço 3 espaço menos espaço 12 x espaço menos espaço 4 m$

Determinando g(f(x))

$g parêntese esquerdo x parêntese direito igual a 3 x espaço mais espaço m g parêntese esquerdo f parêntese esquerdo x parêntese direito parêntese direito igual a 3. f parêntese esquerdo x parêntese direito espaço mais espaço m g parêntese esquerdo f parêntese esquerdo x parêntese direito parêntese direito igual a 3. parêntese esquerdo 3 espaço menos espaço 4 x parêntese direito espaço mais espaço m g parêntese esquerdo f parêntese esquerdo x parêntese direito parêntese direito igual a 9 espaço menos espaço 12 x espaço mais espaço m$

2º passo: igualar as funções e resolver para m

Do enunciado temos:

$f parêntese esquerdo g parêntese esquerdo x parêntese direito parêntese direito espaço igual a espaço g parêntese esquerdo f parêntese esquerdo x parêntese direito parêntese direito 3 espaço menos espaço 12 x espaço menos espaço 4 m espaço igual a espaço 9 espaço menos espaço 12 x espaço mais espaço m 3 espaço riscado diagonal para cima sobre menos espaço 12 x fim do riscado espaço menos espaço 4 m espaço igual a espaço 9 espaço riscado diagonal para cima sobre menos espaço 12 x fim do riscado espaço mais espaço m 3 espaço menos espaço 4 m espaço igual a espaço 9 espaço mais espaço m 3 espaço menos espaço 9 espaço igual a espaço m espaço mais espaço 4 m menos 6 espaço igual a espaço 5 m menos 6 sobre 5 igual a m$

Exercício 2

(Cefet) Se f(x) = x⁵ e g(x) = x – 1, a função composta f[g(x)] será igual a:

a) x⁵ + x – 1
b) x⁶ – x⁵
c) x⁶ – 5x⁵ + 10x⁴ – 10x³ + 5x² – 5x + 1
d) x⁵ – 5x⁴ + 10x³ – 10x² + 5x – 1
e) x⁵ – 5x⁴ – 10x³ – 10x² – 5x – 1

Ver Resposta

Alternativa d: x⁵ – 5x⁴ + 10x³ – 10x² + 5x – 1

Resolução

$f parêntese esquerdo x parêntese direito espaço igual a espaço x à potência de 5 f parêntese esquerdo g parêntese esquerdo x parêntese direito parêntese direito espaço igual a espaço g parêntese esquerdo x parêntese direito à potência de 5 espaço f parêntese esquerdo g parêntese esquerdo x parêntese direito parêntese direito espaço igual a parêntese esquerdo x espaço menos espaço 1 parêntese direito à potência de 5$

Desenvolvendo o binômio, temos:

$parêntese esquerdo x espaço menos espaço 1 parêntese direito à potência de 5 igual a espaço x à potência de 5 fim do exponencial espaço – espaço 5 x à potência de 4 mais espaço 10 x ao cubo espaço – espaço 10 x ao quadrado espaço mais espaço 5 x espaço – espaço 1$

Conheça outros tipos de funções:

Função Inversa

A função inversa é um tipo de função bijetora (sobrejetora e injetora). Isso porque os elementos de uma função A possuem um elemento correspondente de uma função B.

Sendo assim, é possível trocar os conjuntos e associar cada elemento de B com os de A.

A função inversa é representada por $reto f à potência de menos 1 fim do exponencial$ .

Exemplo:
Dada as funções A = {1, 2, 3, 4} e B = {1, 3, 5, 7}, definida pela lei y = 2x – 1, temos:

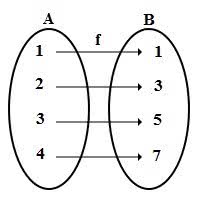
Logo,

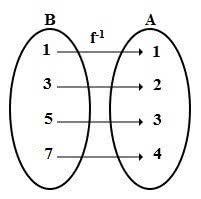
A função inversa f ^-1é dada pela lei:

y = 2x – 1
y +1 = 2x
x = y + 1/2