Domínio, contradomínio e imagem

O domínio, o contradomínio e a imagem são conjuntos de números ligados pelas funções matemáticas.

Quando temos uma função, ela pega os valores de um conjunto chamado domínio e transforma esses valores de acordo com uma regra (ou fórmula). Esses valores transformados “viajam” do domínio até outro conjunto, que chamamos de contradomínio.

No contradomínio, nem todos os números precisam ser usados. O grupo de números que realmente foi transformado pela função e chegou ao contradomínio é chamado de imagem.

Resumindo:

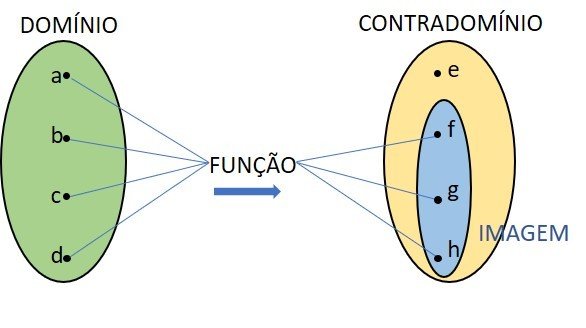
• Domínio: conjunto de onde saem os valores que a função usa;
• Contradomínio: conjunto para onde esses valores transformados vão;
• Imagem: subconjunto no contradomínio com os valores que a função realmente transforma.

Esses três conjuntos podem ser pequenos (finitos) ou muito grandes (infinitos), mas nunca estão vazios.

Quando estudamos funções, é importante dizer quais tipos de números pertencem aos conjuntos envolvidos, como o conjunto dos números naturais (números inteiros positivos) ou o conjunto dos números reais (que inclui todos os números, como inteiros, decimais, etc.).

No caso de funções reais, o domínio é o conjunto de números reais para os quais a expressão da função não gera valores indefinidos (como divisões por zero ou raízes de números negativos no conjunto dos reais).

Imaginemos que temos um domínio A. Cada elemento que pertence a esse domínio, chamado de x, é transformado pela função em outro valor, chamado de y, que faz parte de um contradomínio B. O valor y é chamado de imagem de x.

Para representar isso, usamos a notação (lemos f de A em B):

• A é o conjunto de entrada (domínio),
• B é o conjunto de chegada (contradomínio),
• f é a função que transforma os elementos de A em elementos de B.

Exemplo
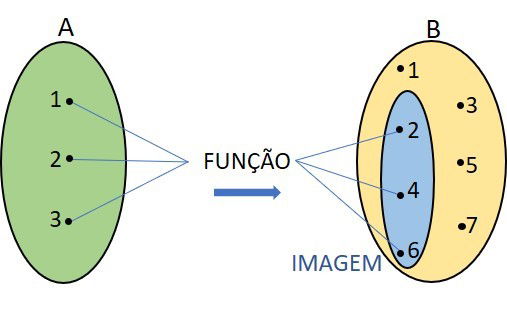
Uma função f:A→B definida pela lei de formação f(x) = 2x, em que seu domínio é o conjunto A={1, 2, 3} e o contradomínio B={1, 2, 3, 4, 5, 6, 7}, pode ser representada pelos valores da tabela e pelos diagramas:

Domínio x	f(x) = 2x	Imagem y
1	f(1) = 2 . 1	2
2	f(2) = 2 . 2	4
3	f(3) = 2 . 3	6

Organizando os resultados da tabela nos diagramas:

A representação da função em um sistema cartesiano, fica assim:

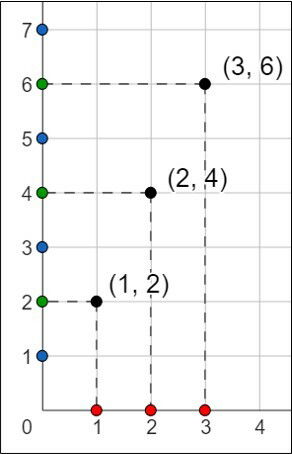
Domínio: os pontos vermelhos no eixo horizontal, também denominado de eixo das abscissas. A função do exemplo está definida para as abscissas: 1, 2 e 3.

Contradomínio: os pontos verdes e azuis no eixo vertical, também chamado de eixo das ordenadas. No exemplo, os pontos: 1, 2, 3, 4, 5 e 6.

Imagem: especificamente os pontos verdes no eixo das ordenadas. No exemplo, os pontos: 2, 4 e 6.

Os pontos pretos são os pares ordenados, com os valores representados em parenteses. O primeiro número nos parenteses é o valor do domínio, o segundo, sua imagem correspondente.

Domínio

O domínio (D) de uma função f é o conjunto de entrada, composto pelos elementos que aplicamos na função, que chamamos de x.

Visualmente, em um gráfico cartesiano, os elementos do domínio são representados no eixo x, também chamado de eixo das abcissas.

Na notação, o domínio é indicado pela letra antes da seta. Por exemplo, na função f: D → CD, o domínio é o D.

Todo valor de x no domínio tem uma imagem correspondente no contradomínio.

Contradomínio

Contradomínio “CD”, é o conjunto de chegada, ou seja, onde os resultados da função, chamados de y, vão parar.

Em um sistema cartesiano, os valores do contradomínio estão no eixo das ordenadas.

Na notação, o contradomínio aparece depois da seta. Por exemplo, na função f: D → CD, o contradomínio é o CD.

Imagem

A imagem (Im) é um subconjunto do contradomínio, formado pelos valores de y que foram realmente gerados pela função. Esses valores podem ser todos os do contradomínio, ou apenas alguns deles.

Assim, a imagem da função f está sempre contida no contradomínio.

Visualmente, no gráfico cartesiano, os valores da imagem são representados no eixo y, chamado também de eixo das ordenadas.

Quando falamos de imagem, é comum dizer que y é o valor que a função f(x) assume. Escrevemos isso como: y = f (x).

Vale lembrar que um mesmo valor de y pode ser a imagem de mais de um valor de x.

Exemplo
Na função definida pela lei , para valores x simétricos do domínio, temos uma única imagem y.

Aprenda mais sobre funções.

Exercícios sobre domínio, contradomínio e imagem

Exercício 1

Dados os conjuntos A = {8, 12, 13, 20, 23} e B = {10, 17, 22, 24, 25, 27, 41, 46, 47, 55}, determine: domínio, o contradomínio e imagem das funções.

a) f: A → B definida por f(x) = 2x + 1

b) f: A → B definida por f(x) = 3x - 14

Exercício 2

Determine o domínio das funções definidas por:

Exercício 3

Dada a função com domínio no conjunto dos inteiros qual é o conjunto imagem de f(x) ?

Pratique exercícios sobre domínio, contradomínio e imagem.

Aprofunde os seus conhecimentos sobre outras funções matemáticas:

• Função Injetora
• Função Sobrejetora
• Função Bijetora
• Função Inversa
• Função Composta
• Função par e função ímpar
• Exercícios de Função Afim (Função do 1º Grau)

Aplicações e curiosidades

As funções possuem aplicação no estudo de qualquer fenômeno em que um parâmetro dependa de outro. Como, por exemplo, a velocidade de um móvel com o passar do tempo, os efeitos de um fármaco com as características de acidez no estômago, a temperatura de uma caldeira com a quantidade de combustível.

As funções estão presentes nos fenômenos reais e, por isto, possuem aplicação em todo estudo científico e de engenharia.

O estudo das funções não é recente, alguns registros na Antiguidade em tábuas babilônicas mostram que já faziam parte da matemática. Com o passar dos anos a notação, maneira como se escrevem, foi recebendo contribuições de diversos matemáticos e se aprimorando, até como as utilizamos hoje.