Função Linear

A Função Linear é uma função f : ℝ→ℝ definida como f(x) = a.x, sendo a um número real e diferente de zero. Esta função é um caso particular da função afim f(x) = a.x + b, quando b = 0.

O número a que acompanha o x da função é chamado de coeficiente. Quando seu valor for igual a 1, a função linear será também chamada de função identidade ou função constante.

O conjunto domínio das funções lineares são todos os números reais (R), assim como o contradomínio e a imagem.

A função linear é amplamente utilizada para descrever fenômenos de crescimento ou decrescimento constante, como velocidades, taxas de variação e custos proporcionais quando os valores iniciais são iguais a zero.

Exemplo de problema de função linear:

Em uma loja são vendidos relógios, cujo preço de venda é igual a R$ 40,00. O valor da receita total da venda desses relógios é obtida multiplicando-se o preço de cada unidade pela quantidade vendida. Considerando x a quantidade vendida, determine:

a) uma função que represente a situação descrita.
b) o tipo de função encontrada.
c) o valor da receita quando forem vendidos 350 relógios.

Resolução

a) O valor da receita total em função da quantidade vendida pode ser representada por: f(x) = 40.x

A cada unidade vendida x, aumentamos R$ 40,00. Assim, para saber a receita de x unidades, basta multiplicar 40 por x.

b) A função encontrada é uma função do 1º grau, sendo o valor de b = 0. Desta forma, é uma função linear.
c) Para encontrar a receita correspondente a venda de 350 relógios, basta substituir este valor na expressão encontrada. Assim:

f(x) = 40 . 350 = 14 000

Portanto, ao vender 350 relógios, a receita bruta da loja será igual a R$ 14 000,00.

Gráfico da Função Linear

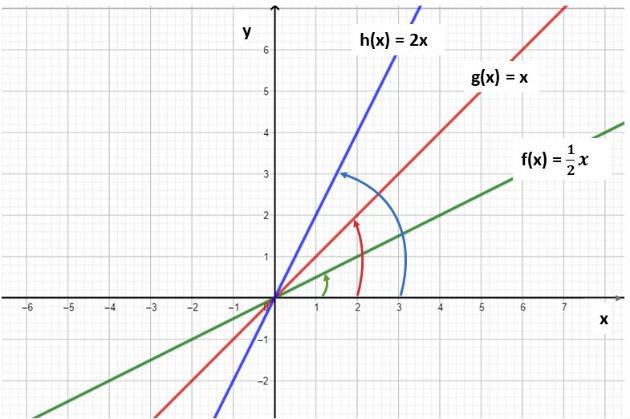
O gráfico da função linear é uma reta que passa pela origem, ou seja, pelo ponto (0,0). O coeficiente a da função, corresponde a inclinação desta reta.

Abaixo, representamos a função f(x) = 1/2 x, g(x) = x (função identidade) e h(x) = 2x. Note que quanto maior o valor do a, maior é a inclinação da reta.

Função Crescente e Decrescente

As funções lineares serão crescentes quando ao aumentarmos o valor do x, o valor da função também aumenta. Por outro lado, serão decrescentes quando aumentado o x a função diminuirá.

Para sabermos se uma função linear é crescente ou decrescente, basta identificar o sinal do coeficiente. Se a for positivo, a função será crescente, se for negativo será decrescente.

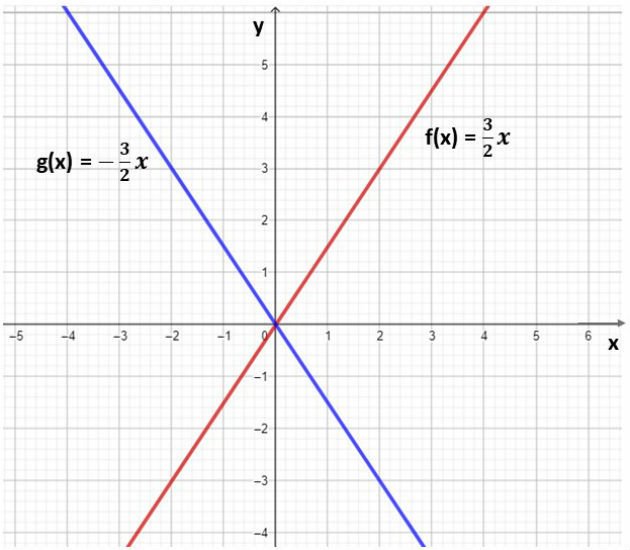
• a > 0: A função é crescente (reta sobe da esquerda para a direita).
• a < 0: A função é decrescente (reta desce da esquerda para a direita).
• a = 0 A função é constante.

Abaixo, apresentamos o gráfico da função f(x) = 3/2.x e g(x) = - 3/2.x:

Inclinação da reta (Coeficiente Angular a)

A inclinação determina o "quão inclinada" é a reta. O valor desta inclinação está associado ao parâmetro a, chamado coeficiente angular.

O coeficiente angular é calculado pela fórmula:

Ou seja, a inclinação é a razão entre a variação em y e a variação em x.

Aprenda o que é função.

Exercícios de Função Linear

Exercício 1

(Fuvest) A função que representa o valor a ser pago após um desconto de 3% sobre o valor x de uma mercadoria é:

a) f(x) = x - 3
b) f(x) = 0,97x
c) f(x) = 1,3x
d) f(x) = -3x
e) f(x) = 1,03x

Exercício 2

(Fatec) Na figura a seguir tem-se o gráfico da função f, onde f(x) representa o preço pago em reais por x cópias de um mesmo original, na Copiadora Reprodux.

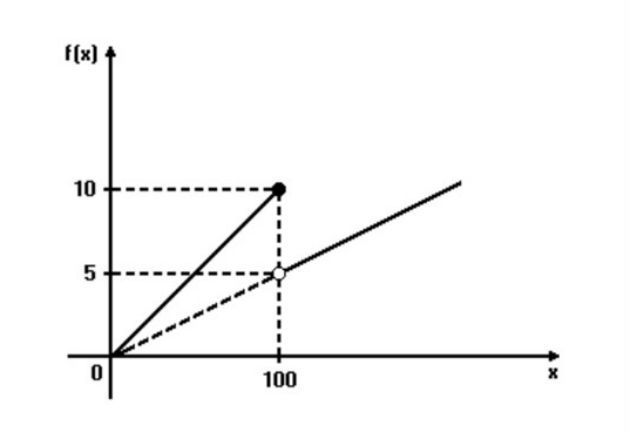
De acordo com o gráfico, é verdade que o preço pago nessa Copiadora por

a) 228 cópias de um mesmo original é R$22,50.
b) 193 cópias de um mesmo original é R$9,65.
c) 120 cópias de um mesmo original é R$7,50.
d) 100 cópias de um mesmo original é R$5,00
e) 75 cópias de um mesmo original é R$8,00.

Para saber mais, leia também:

• Função Afim
• Função Modular
• Exercícios de função modular
• Função Quadrática
• Função Quadrática - Exercícios
• Função Exponencial
• Exercícios de Função Afim
• Equação do 2º Grau - Exercícios
• Função Exponencial - Exercícios
• Fórmulas de Matemática