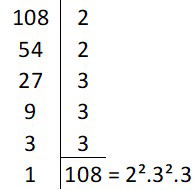23 exercícios de Matemática para 7º ano (questões resolvidas e explicadas)

Rafael C. Asth

Professor de Matemática e Física

Estude com os 23 exercícios de Matemática do 7º ano do Fundamental com os temas estudados na escola. Tire todas suas dúvidas com os exercícios com gabarito e explicados passo a passo.

Os exercícios estão de acordo com a BNCC (Base Nacional Comum Curricular). Em cada exercício você encontra o código da habilidade trabalhada. Utilize em suas aulas e planejamentos ou como reforço escolar.

Exercício 1 (MDC - Máximo Divisor Comum)

Habilidade BNCC EF07MA01

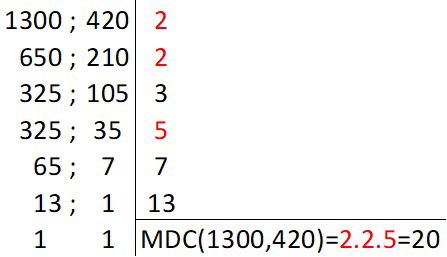
Em uma confecção estão sendo produzidas blusas de duas cores com a mesma quantidade de tecido para cada cor. No estoque, há um rolo de tecido branco com 4,2 m e um rolo de tecido azul com 13 m. Os tecidos devem ser cortados em tiras com o mesmo e, maior comprimento possível, sem sobrar nenhum pedaço nos rolos. Em centímetros, cada tira de tecido terá

a) 150 cm.
b) 115 cm.
c) 20 cm.
d) 60 cm.
e) 32 cm.

Ver Resposta

Resposta correta: c) 20 cm

Para determinar o comprimento das tiras, sendo estas de mesmo e maior tamanho possível, sem sobrar tecido nos rolos, devemos determinar qual o MDC entre 420 cm e 1 300 cm.

Fatoração entre 420 e 1 300.

Fatorando os dois números ao mesmo tempo, destacando os divisores comuns a ambos e os multiplicando:

Fatoração em 1300 e 420. — No MDC, multiplicamos apenas os divisores comuns.

Portanto, as tiras devem possuir 20 cm para que não sobre tecido nos rolos, possuindo o maior tamanho possível.

Exercício 2 (MMC - Mínimo Múltiplo comum)

Habilidade BNCC EF07MA01

Gabriel e Osvaldo são motoristas de ônibus em linhas diferentes. Logo no início do dia, às 6h, eles combinaram de tomar um café na rodoviária na próxima vez que se encontrarem. Acontece, que a viagem que Osvaldo faz é mais longa e ele demora 2h para estar de volta a rodoviária, enquanto Gabriel, está na rodoviária a cada 50 minutos. A partir das 6h, os amigos poderão tomar o café às

a) 6h.
b) 8h.
c) 10h.
d) 12h.
e) 16h.

Ver Resposta

Resposta correta: e) 16h.

Para determinar quando os dois amigos irão se encontrar novamente na rodoviária, devemos encontrar o MMC - Menor Múltiplo Comum entre 2h, ou 120 min e, 50 min.

Fatoração entre 120 e 50.

Sendo assim, eles se encontrarão após 600 min ou, 10 h.

Contando a partir das 6h, eles se encontrarão na rodoviárias às 16h.

Exercício 3 (Retas Paralelas Cortadas por uma Transversal)

A reta t é transversal as paralelas u e v. Marque a opção que determina as medidas dos ângulos $teta$ e $alfa$ , nesta ordem.

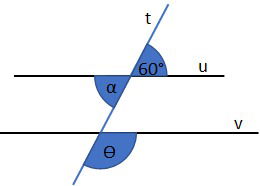
Habilidade BNCC EF07MA23

a) 180° e 60°.
b) 60° e 90°.
c) 90° e 180°.
d) 120° e 60°.
e) 30° e 150°.

Ver Resposta

Resposta correta: d) 120° e 60°.

O ângulo $alfa$ é oposto pelo vértice ao de 60°, por isso, também possui 60°.

O ângulo $teta$ é colateral externo com o ângulo de 60°. Estes ângulos são suplementares, ou seja, somados resultam em 180°. Por isso, $teta$ = 120, pois

$60 sinal de grau espaço mais espaço teta espaço igual a espaço 180 sinal de grau teta espaço igual a espaço 180 sinal de grau espaço menos espaço 60 sinal de grau teta espaço igual a espaço 120 sinal de grau$

Exercício 4 (Medida de Comprimento)

Habilidade BNCC EF07MA29

Neste último domingo, Caio saiu para andar de bicicleta e decidiu ir até à casa de seu amigo José, percorrendo 1,5 km. De lá, os dois pedalaram até a casa de Sabrina, que ficava no quarteirão ao lado, 3 hm depois. Os três amigos decidiram ir até o alto da serra da cidade, pedalando mais 4 km. De casa, até o alto da serra, Caio pedalou quantos metros?

a) 5 500 m
b) 5 800 m
c) 5 303 m
d) 5 530 m
e) 8 500 m

Ver Resposta

Resposta correta: b) 5 800 m

Primeiro transformamos as medidas para metros.

1,5 km = 1 500 m
3 hm = 300 m
4 km = 4 000 m

$1 espaço 500 espaço reto m espaço mais espaço 300 espaço reto m espaço mais espaço 4000 espaço reto m espaço igual a espaço 5 espaço 800 espaço reto m$

Exercício 5 (Medida de Tempo)

Habilidade BNCC EF07MA29

Maria deixará seu filho no cinema assistindo o novo filme dos Super-Heróis Radicais enquanto compra algumas coisas no Shopping. Ela já sabe que o filme tem 2h 17min, tempo suficiente para realizar as compras. Transformando em segundos, o filme tem

a) 8 220 s.
b) 8 100 s.
c) 7 200 s.
d) 7 350 s.
e) 4 620 s.

Ver Resposta

Resposta correta: a) 8 220 s.

Primeiro transformamos em minutos.

2h 17min = 60 min + 60 min + 17 min = 137 min

Cada minuto possui 60 segundos. Multiplicamos por 60.

137 min x 60 s = 8 220 s

Exercício 6 (Medida de Massa)

Habilidade BNCC EF07MA29

Em uma viagem de 900 km, o computador de bordo de um carro exibiu uma emissão de 117 kg de gás carbônico. Algum tempo depois, esse equipamento se danificou e não estava calculando esta informação. Com base nos dados obtidos em sua viagem, o proprietário do automóvel calculou a quantidade de CO2 emitido em um passeio de 25 km, encontrando em gramas, a quantidade de

a) 3 250 g.
b) 192 307 g.
c) 325 g.
d) 192 g.
e) 32,5 g.

Ver Resposta

Resposta correta: a) 3 250 g

1° passo: quantidade de CO2 emitido por quilômetro rodado.

$117 espaço kg espaço dividido por espaço 900 espaço km espaço igual a espaço 0 vírgula 13 espaço kg dividido por km$

2° passo: quantidade de CO2 emitido em 25 km.

$0 vírgula 13 espaço kg sobre km sinal de multiplicação 25 espaço km espaço igual a espaço 3 vírgula 25 espaço kg$

3° passo: transformando de kg para g.

Para transformar de kg para g, multiplicamos por 1 000.

3,25 kg = 3 250 g

Portanto, a quantidade em gramas de CO2 emitido pelo veículo em um passeio de 25 km é 3 250 g.

Exercício 7 (Volume)

Habilidade BNCC EF07MA30

Uma empreiteira está construindo um edifício e fechou uma compra de pedra brita, material necessário para fazer o concreto. A brita, é entregue em caminhões, com caçambas na forma de paralelepípedos de 3 m x 1,5 m x 1 m. Os engenheiros calcularam um volume total de 261 m³ de brita para realizar a obra. A quantidade de caminhões que a empreiteira teve de contratar foi

a) 81.
b) 64.
c) 36.
d) 48.
e) 58.

Ver Resposta

Resposta correta: e) 58.

O volume de um paralelepípedo é calculado multiplicando as medidas das três dimensões.

O volume da caçamba de um caminhão é de:

V = comprimento x largura x altura
V = 3 x 1,5 x 1 = 4,5 m³

Dividindo o volume total calculado para a obra, de 261 m³ pelo volume de uma caçamba

$numerador 261 sobre denominador 4 vírgula 5 fim da fração igual a 58$

A empresa deve contratar 58 caminhões de brita.

Exercício 8 (Capacidade)

Habilidade BNCC EF07MA29

Em uma corrida de longa distância, é comum a distribuição de água aos atletas. O pessoal de apoio oferece garrafas ou copos com água na beira da pista, para que os corredores possam se hidratar sem parar de correr. Em uma maratona, os organizadores distribuíram 3 755 copos com 275 ml de água em cada. A quantidade de água, em litros, consumida durante a corrida foi de, aproximadamente

a) 1 l
b) 103,26 l
c) 1 033 l
d) 10,32 l
e) 10 326 l

Ver Resposta

Resposta correta: c) 1 033 l

A quantidade total em mililitros foi de $3 espaço 755 espaço sinal de multiplicação espaço 275 espaço igual a espaço 1 espaço 032 espaço 625 espaço ml$ .

Para transformar a medida de mililitros para litros, dividimos por 1 000.

$1 espaço 032 espaço 625 espaço dividido por espaço 1 espaço 000 espaço igual a espaço 1 espaço 032 vírgula 625 espaço l$

Aproximadamente, 1 033 l.

Exercício 9 (Área do Retângulo e Paralelogramo)

Habilidade BNCC EF07MA31

A prefeitura da cidade dispõe de um terreno na forma de um paralelogramo. Foi decidido que uma quadra poliesportiva será construída no local, com arquibancadas nas laterais. Os espaços que sobraram, serão ornamentados com jardins. Conforme a planta baixa do projeto, cada jardim ocupará uma área de

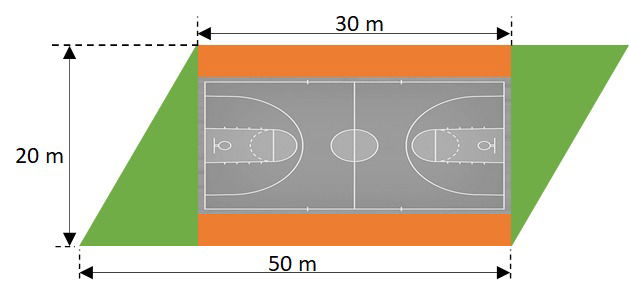
a) 200 m².
b) 250 m².
c) 300 m².
d) 350 m².
e) 400 m².

Ver Resposta

Resposta correta: a) 200 m².

1° passo: área do paralelogramo.

$reto A com paralelogramo subscrito igual a reto b. reto h igual a 50 espaço reto m espaço. espaço 20 espaço reto m igual a 1000 espaço reto m ao quadrado$

2° passo: área do retângulo e arquibancadas.

$reto A com retângulo subscrito igual a reto b. reto h igual a 30 espaço reto m espaço. espaço 20 espaço reto m espaço igual a espaço 600 espaço reto m ao quadrado$

3° passo: área dos jardins, em verde.

Fazendo a subtração entre a área total e a área do retângulo.

$reto A com jardins subscrito igual a 1000 menos 600 igual a 400 espaço reto m ao quadrado$

Portanto, como os triângulos são iguais, a área de cada jardim é de 200 m².

Exercício 10 (Área do Losango)

Habilidade BNCC EF07MA31

Sr. Pompeu gosta de fazer pipas. No final de semana, haverá uma feira de pipas e ele irá levar algumas. Quantos centímetros quadrados de papel de seda ele utiliza para fazer uma pipa, de acordo com o modelo? Marque a opção correta.

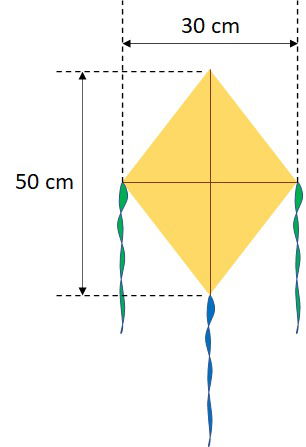
a) 7,5 m²
b) 0,075 m².
c) 0,15 m².
d) 0,75 m²
e) 1,5 m²

Ver Resposta

Resposta correta: b) 0,075 m².

A pipa possui a forma de um losango. As medidas das diagonais estão na figura, em centímetros.

A área de um losango é calculada por:

$reto A com losango subscrito igual a numerador reto D. reto d sobre denominador 2 fim da fração reto A com losango subscrito igual a numerador 50.30 sobre denominador 2 fim da fração igual a numerador 1 espaço 500 sobre denominador 2 fim da fração igual a 750 espaço cm ao quadrado$

Portanto, em metros quadrados, a área da pipa é de 0,075 m².

Exercício 11 (Área do Triângulo e do Hexágono)

Habilidade BNCC EF07MA32

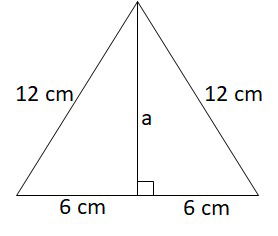
Um hexágono regular é formado por seis triângulos equiláteros com os lados medindo 12 cm. A área do hexágono é igual a

a) $216 espaço cm ao quadrado$ .
b) $216 raiz quadrada de 3 cm ao quadrado$ .
c) $6 raiz quadrada de 108 cm ao quadrado$ .
d) $18 raiz quadrada de 3 cm ao quadrado$ .
e) $18 raiz quadrada de 108 cm ao quadrado$ .

Ver Resposta

Resposta correta: b) $216 raiz quadrada de 3 cm ao quadrado$ .

Devemos calcular a área de um triângulo retângulo e multiplicar por seis.

1° passo: determinar a altura do triângulo.

Para calcular a altura, utilizamos o Teorema de Pitágoras.

$12 ao quadrado igual a a ao quadrado mais 6 ao quadrado 144 espaço menos espaço 36 espaço igual a a ao quadrado 108 espaço igual a espaço a ao quadrado raiz quadrada de 108 igual a a$

Assim, a altura do triângulo mede $raiz quadrada de 108$ cm.

2° passo: calcular a área de um triângulo equilátero.

A área é calculada pelo produto da base e altura, dividido por dois.

$reto A com triângulo subscrito igual a numerador reto b. reto a sobre denominador 2 fim da fração$

$reto A com triângulo subscrito igual a numerador 12. raiz quadrada de 108 sobre denominador 2 fim da fração reto A com triângulo subscrito igual a 6 raiz quadrada de 108 espaço cm ao quadrado$

3° passo: calcular a área do hexágono.

Multiplicando a área do triângulo por seis, temos:

$6 espaço x espaço 6 raiz quadrada de 108 espaço igual a espaço 36 raiz quadrada de 108 espaço cm ao quadrado$

A raiz quadrada de 108 não tem solução exata, mas é comum fatorar o radical.

$36 espaço. raiz quadrada de 108 igual a 36 espaço. raiz quadrada de 2 ao quadrado. espaço 3 à potência de 2 espaço fim do exponencial.3 fim da raiz igual a 36 espaço. espaço raiz quadrada de 2 ao quadrado fim da raiz. raiz quadrada de 3 ao quadrado fim da raiz. raiz quadrada de 3 espaço igual a 36 espaço. espaço 2 espaço. espaço 3 espaço. espaço raiz quadrada de 3 igual a 216 raiz quadrada de 3$

Sendo assim, a área do hexágono é de $216 raiz quadrada de 3 cm ao quadrado$ .

Exercício 12 (Comprimento da Circunferência)

Habilidade BNCC EF07MA33

As bicicletas possuem uma numeração que identifica o tamanho de suas rodas. Uma bicicleta aro 20 tem rodas com 20 polegadas de diâmetro, enquanto uma bicicleta aro 26, tem rodas com diâmetro de 26 polegadas. Qual a diferença entre os comprimentos das circunferências das rodas de uma bicicleta aro 26 e 20, em centímetros.

Dado: 1 polegada = 2,54 cm e $pi$ = 3,14.

a) 47,85 cm
b) 18,84 cm
c) 29,64 cm
d) 34,55 cm
e) 55,17 cm

Ver Resposta

Resposta correta: a) 47,85 cm

O comprimento da circunferência é calculado pela relação

$C com c i r c u n f e r ê n c i a subscrito fim do subscrito igual a 2. pi. r$

O raio da bicicleta aro 26 é 13 polegadas.
O raio da bicicleta aro 20 é 10 polegadas.

1° passo: cálculo da circunferência da bicicleta aro 26.

$reto C com circunferência subscrito igual a 2. reto pi. reto r reto C com circunferência subscrito igual a 2.3 vírgula 14.13 igual a 81 vírgula 64 espaço pol$

2° passo: cálculo da circunferência da bicicleta aro 20.

$reto C com circunferência subscrito igual a 2. reto pi. reto r espaço igual a 2.3 vírgula 14.10 espaço igual a 62 vírgula 8 espaço espaço$

3° passo: diferença entre as circunferências

$81 vírgula 64 espaço menos espaço 62 vírgula 8 espaço igual a espaço 18 vírgula 84 espaço pol$

4° passo: passando para centímetros

$18 vírgula 84 espaço sinal de multiplicação espaço 2 vírgula 54 espaço aproximadamente igual espaço 47 vírgula 85 espaço cm espaço$

Exercício 13 (Condição de Existência de Triângulos)

Habilidade BNCC EF07MA25

Dos seguintes trios de medidas a seguir, é possível montar um triângulo apenas com

a) 7, 3, 14.
b) 19, 3, 6.
c) 8, 15, 45.
d) 12, 15, 17.
e) 21, 13, 7.

Ver Resposta

Resposta correta: d) 12, 15, 17.

Para determinar se um triângulo pode ser construído a partir de três medidas, fazemos três testes. A medida de cada lado deve ser menor do que a soma dos outros dois lados.

Teste 1: 12 < 15 + 17

Teste 2: 15 < 12 + 17

Teste 3: 17 < 15 + 12

Como as desigualdades dos três testes são verdadeiras, um triângulo com estas medidas existe.

Exercício 14 (Soma dos Ângulos de Triângulos)

Habilidade BNCC EF07MA24

No triângulo da figura, determine o valor dos ângulos dos vértices A, B e C e marque a opção correta.

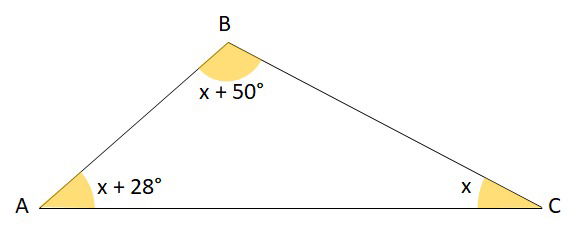
Triângulo com ângulos desconhecidos em função de x. — Imagem fora de escala.

a) A = 64°, B = 34° e C = 82°
b) A = 62°, B = 84° e C = 34°
c) A = 53°, B = 62° e C = 65°
d) A = 34°, B = 72° e C = 74°
e) A = 34°, B = 62° e C = 84°

Ver Resposta

Resposta correta: b) A = 62°, B = 84° e C = 34°.

A soma de todos os ângulos internos de um triângulo sempre resulta em 180°.

$x espaço mais espaço parêntese esquerdo x espaço mais espaço 28 sinal de grau parêntese direito espaço mais espaço parêntese esquerdo x espaço mais espaço 50 sinal de grau parêntese direito espaço igual a espaço 180 sinal de grau 3 x espaço mais espaço 78 sinal de grau espaço igual a espaço 180 sinal de grau 3 x espaço igual a espaço 180 sinal de grau espaço menos espaço 78 sinal de grau 3 x espaço igual a espaço 102 sinal de grau x espaço igual a espaço 34 sinal de grau$

Logo,

A = x + 28 = 34 + 28 = 62°
B = x + 50 = 34 + 50 = 84°
C = x = 34°

Exercício 15 (Equação do 1° grau)

Habilidade BNCC EF07MA18

Utilizando equações do 1° grau com uma incógnita, expresse cada situação abaixo e determine sua raiz.

a) Um número subtraído de sua terça parte, mais seu dobro é igual a 26.
b) O quádruplo de um número adicionado ao próprio número e subtraído de um quinto do número é igual a 72.
c) O terço de um número adicionado ao seu quíntuplo é igual a 112.

Ver Resposta

a)
$bold italic x negrito espaço negrito menos negrito espaço negrito x sobre negrito 3 negrito espaço negrito mais negrito espaço negrito 2 bold italic x negrito espaço negrito igual a negrito espaço negrito 26 numerador 3 reto x sobre denominador 3 fim da fração menos reto x sobre 3 mais numerador 6 reto x sobre denominador 3 fim da fração igual a 26 numerador 8 reto x sobre denominador 3 fim da fração igual a 26 8 reto x igual a 26.3 8 reto x igual a 78 reto x igual a 78 sobre 8 igual a 9 vírgula 75$

$negrito 4 negrito x negrito espaço negrito mais negrito espaço negrito x negrito espaço negrito menos negrito espaço negrito x sobre negrito 5 negrito igual a negrito 72 numerador 20 reto x sobre denominador 5 fim da fração mais numerador 5 reto x sobre denominador 5 fim da fração menos reto x sobre 5 igual a 72 numerador 24 reto x sobre denominador 5 fim da fração igual a 72 24 reto x espaço igual a espaço 360 reto x igual a 360 sobre 24 igual a 15$

$negrito x sobre negrito 3 negrito mais negrito 5 negrito x negrito igual a negrito 112 reto x sobre 3 mais numerador 15 reto x sobre denominador 3 fim da fração igual a 112 numerador 16 reto x sobre denominador 3 fim da fração igual a 112 16 reto x igual a 112 espaço. espaço 3 16 reto x igual a 336 reto x igual a 336 sobre 16 igual a 21$

Exercício 16 (Equação do 1° grau)

Habilidade BNCC EF07MA18 e EF07MA16

Três números consecutivos somados resultam em 57. Determine quais são os números desta sequência.

a) 21, 22 e 23
b) 10, 11 e 12
c) 27, 28 e 29
d) 18, 19 e 20
e) 32, 33 e 34

Ver Resposta

Resposta correta: d) 18, 19 e 20

Chamando de x o número do meio da sequência, temos:

$negrito parêntese esquerdo negrito x negrito espaço negrito menos negrito espaço negrito 1 negrito parêntese direito negrito espaço negrito mais negrito espaço negrito x negrito espaço negrito mais negrito espaço negrito parêntese esquerdo negrito x negrito espaço negrito mais negrito espaço negrito 1 negrito parêntese direito negrito espaço negrito igual a negrito espaço negrito 57 espaço espaço 3 x igual a 57 espaço x igual a 57 sobre 3 igual a 19$

Substituindo 19 por x na primeira linha, encontramos:

(19 - 1) + 19 + (19 + 1) = 57

Dessa forma, os números são:

18, 19 e 20

Exercício 17 (Razão)

Habilidade BNCC EF07MA09

A turma de Mariana na escola tem 23 alunos dos quais 11 são meninos. A razão entre o número de meninos e meninas na turma de Mariana é

a) 11/23
b) 12/23
c) 12/11
d) 11/12
e) 12/12

Ver Resposta

Resposta correta: d) 11/12

Razão é uma relação descrita através de uma fração.

Como na sala de Mariana há 23 alunos e 11 são meninos, o número de meninas é:

23 -11=12

Portanto, há 11 meninos para cada 12 meninas. A razão entre o número de meninos e meninas na sala de Mariana é:

$11 sobre 12$

Exercício 18 (Razão)

Habilidade BNCC EF07MA09

Segundo dados do IBGE a estatística populacional do Brasil em 2021 é de 213,3 milhões de habitantes. A área aproximada do território brasileiro é de 8.516.000 km². Com base nestes dados, a densidade demográfica brasileira é de

a) 15 pessoas.
b) 20 pessoas.
c) 25 pessoas.
d) 40 pessoas.
e) 45 pessoas.

Ver Resposta

Resposta correta: 25 pessoas.

Densidade demográfica é a quantidade de pessoas que vivem em uma área. Queremos determinar segundo a estatística populacional do IBGE para o ano de 2021, quantas pessoas vivem por quilômetro quadrado no Brasil.

Em forma de razão, temos:

$numerador 213 espaço 300 espaço 000 sobre denominador 8 espaço 516 espaço 000 fim da fração aproximadamente igual 25$

Portanto, a densidade demográfica no ano de 2021 é de, aproximadamente, 25 pessoas por quilômetro quadrado.

Exercício 19 (Proporção - Grandezas Diretamente proporcionais)

Habilidade BNCC EF07MA17

Se um veículo possuí autonomia de 12 km com um litro de combustível, com 23 litros, este veículo poderá percorrer, sem parar para abastecer

a) 113 km.
b) 156 km.
c) 276 km
d) 412 km.
e) 120 km.

Ver Resposta

Resposta correta: c) 276 km.

A proporcionalidade é direta entre as grandezas litros de combustível e quilômetros percorridos pois, quanto mais combustível, maior distância o veículo pode se mover.

Montamos a proporção entre as razões:

Um litro está para 12 km, assim como, 23 litros está para x.

$numerador 1 espaço l i t r o espaço seta para a direita espaço 12 espaço k m sobre denominador 23 espaço l i t r o s espaço seta para a direita espaço x espaço k m fim da fração 1 sobre 23 igual a 12 sobre x$

Utilizando a propriedade fundamental das proporções (multiplicação cruzada), determinamos o valor de x.

$1 espaço. espaço x espaço igual a espaço 23 espaço. espaço 12 x espaço igual a espaço 276$

Sendo assim, com 23 litros de combustível, o veículo poderá percorrer 276 km.

Exercício 20 (Porcentagem)

Habilidade BNCC EF07MA02

O combustível utilizado nos veículos automotores é, na verdade, uma mistura, mesmo quando o consumidor compra gasolina em um posto de combustível. Isso porque a Lei 10.203/01 instituiu que a gasolina deve conter entre 20% a 24% de álcool combustível. Após, a Agência Nacional do Petróleo (ANP) fixou em 23% a mistura álcool-gasolina.

Se um cliente em um posto de combustível pede para o frentista completar o tanque com gasolina e, a bomba marca 50 litros, destes, a quantidade real de gasolina pura é

a) 11,5 l.
b) 38,5 l.
c) 45,5 l.
d) 35,5l.
e) 21,5 l.

Ver Resposta

Resposta correta: b) 38,5 l.

Segundo a ANP, a porcentagem de álcool misturado na gasolina é de 23%.

$23 sobre 100 sinal de multiplicação 50 espaço igual a numerador 23 espaço sinal de multiplicação 50 sobre denominador 100 fim da fração igual a numerador 1 espaço 150 sobre denominador 100 fim da fração igual a 11 vírgula 5$

A cada 50 litros, 11,5 l são de álcool.

Sendo assim, dos 50 litros de combustível abastecidos, a quantidade de gasolina pura é de

$50 espaço menos espaço 11 vírgula 5 espaço igual a espaço 38 vírgula 5 espaço l$

Exercício 21 (Proporção - Grandezas Inversamente Proporcionais)

Habilidade BNCC EF07MA17

Um trem percorre 90 km em 1,5 h com uma velocidade constante de 60 km/h. Suponha que uma pessoa tenha percorrido de carro a mesma distância com velocidade de 100 km/h. O tempo desta viagem em horas será de

a) 30 min.
b) 43 min.
c) 54 min.
d) 61 min.
e) 63 min.

Ver Resposta

Resposta correta: c) 54 min.

A grandeza tempo é inversa a velocidade pois, quanto maior a velocidade menor o tempo da viagem.

Montamos a proporção entre as razões:

60 km/h está para 1,5h de viagem, assim como, 100 km/h está para x.

$60 espaço k m dividido por h espaço seta para a direita espaço 1 vírgula 5 h 100 espaço k m dividido por h espaço seta para a direita espaço x$

Atenção, como as grandezas são inversas, devemos inverter a razão onde está a incógnita.

$60 sobre 100 igual a numerador 1 vírgula 5 sobre denominador x fim da fração i n v e r t e n d o espaço a espaço r a z ã o espaço c o m espaço a espaço i n c ó g n i t a espaço 60 sobre 100 igual a numerador x sobre denominador 1 vírgula 5 fim da fração$

Aplicando a propriedade fundamental das proporções, fazemos o produto dos meios igual ao produto dos extremos.

$60 espaço. espaço 1 vírgula 5 espaço igual a espaço 100 espaço. espaço x 90 espaço igual a espaço 100 espaço. espaço x 90 sobre 100 igual a x 0 vírgula 9 espaço igual a espaço x$

Sendo assim, a pessoa que percorreu o mesmo trajeto com velocidade de 100 km/h, levou 0,9 h para completar o trajeto.

Transformando em minutos

0,9 x 60 = 54

Em minutos, a pessoa que viajou de carro levou 54 min para completar o percurso.

Exercício 22 (Regra de Três Composta)

Habilidade BNCC EF07MA17

Em uma confecção seis costureiras produzem 1200 peças em três dias de trabalho. O número de peças produzidas por oito costureiras em nove dias será de

a) 4 800 peças.
b) 1 600 peças.
c) 3 600 peças.
d) 2 800 peças.
e) 5 800 peças.

Ver Resposta

Resposta correta: a) 4 800 peças.

O número de peças é diretamente proporcional ao número de costureiras e dias de trabalho.

nº de costureiras	nº de dias de trabalho	nº de peças
6	3	1 200
8	9	x

Temos dois modos de resolver.

1º modo

A razão da incógnita x, é igual ao produto das outras razões.

$numerador 1 espaço 200 sobre denominador reto x fim da fração igual a numerador 6 espaço. espaço 3 sobre denominador 8 espaço. espaço 9 fim da fração numerador 1 espaço 200 sobre denominador reto x fim da fração igual a 18 sobre 72 18 espaço. espaço reto x espaço igual a espaço 1 espaço 200 espaço. espaço 72 18 reto x espaço igual a espaço 86 espaço 400 reto x espaço igual a numerador 86 espaço 400 sobre denominador 18 fim da fração igual a 4 espaço 800$

2º modo

Fazemos a igualdade entre a razão da incógnita e outra qualquer, fixando uma grandeza.

Fixando em três dias.

Em três dias, seis costureiras produzem 1 200 peças, assim como, 8 costureiras produzem x.

$6 sobre 8 igual a numerador 1 espaço 200 sobre denominador x fim da fração 6 espaço. espaço x espaço igual a espaço 8 espaço x espaço 1 espaço 200 6 x espaço igual a espaço 9 espaço 600 x espaço igual a espaço numerador 9 espaço 600 sobre denominador 6 fim da fração igual a 1 espaço 600$

Sabemos agora que oito costureiras produzem 1 600 peças em três dias mas, queremos saber quantas peças as 8 costureiras produzem em nove dias. Agora, utilizamos a outra razão.

Oito costureiras produzem 1 600 peças em três dias, assim como, produzem x peças em nove dias.

$numerador 1 espaço 600 sobre denominador x fim da fração igual a 3 sobre 9 1 espaço 600 espaço. espaço 9 espaço igual a espaço 3 espaço. espaço x 14 espaço 400 espaço igual a espaço 3 x numerador 14 espaço 400 sobre denominador 3 fim da fração igual a x 4 espaço 800 igual a x$

Portanto, oito costureiras trabalhando nove dias produzem 4 800 peças.

Exercício 23 (Probabilidade)

Habilidade BNCC EF07MA36

Uma pesquisa realizada com moradores de duas cidades em relação às marcas de dois cafés, entrevistou moradores em relação às suas preferências. O resultado se encontra na tabela:

	Café Doce Sabor	Especiaria Café
Moradores da cidade A	75	25
Moradores da cidade B	55	65

Habilidade BNCC EF07MA34 e EF07MA36

A marca Especiaria Café irá sortear um kit de produtos para um dos entrevistados. A probabilidade do sorteado ter como preferência esta marca e ainda ser morador da cidade A é

a) 16,21%
b) 15,32%
c) 6,1%
d) 25,13%
e) 11,36%

Ver Resposta

Reposta correta: e) 11,36%

Seja o experimento aleatório sortear um entrevistado ao acaso, o evento C é o sorteado ser da cidade A e preferir o Especiaria Café.

O número de elementos do espaço amostral é:

75 + 25 + 55 + 65 = 220

A probabilidade de ocorrer o evento C, é calculada por:

$P parêntese esquerdo C parêntese direito igual a 25 sobre 220 igual a 5 sobre 44$

Para determinar a porcentagem, dividimos o numerador pelo denominador e, multiplicamos o resultado por 100.

$5 dividido por 44 aproximadamente igual 0 vírgula 1136 0 vírgula 1136 espaço x espaço 100 espaço aproximadamente igual 11 vírgula 36 sinal de percentagem$

Por isso, a probabilidade do sorteado ter como preferência o Especiaria Café e, ainda ser morador da cidade A é de 11,36%.

Veja também

Faça também nosso Simulado Enem de Matemática

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações