Atividades de Matemática do 6º ano (com questões resolvidas)
Confira esta lista de exercícios de Matemática para o 6.º ano com todos os conteúdos ensinados na escola. Estude e tire suas dúvidas com os 31 problemas de Matemática resolvidos e explicados.
Aos professores, as atividades são alinhadas à BNCC. Ao final de cada atividade você encontra a habilidade da BNCC trabalhada. Utilize em seus planos de aula como exercícios, avaliações, revisões ou, como preferirem.
Exercício 1 (números naturais) - fácil
Uma confecção que produz biquínis, teve uma produção de 12 567 peças no mês de janeiro. No mês de fevereiro, como a procura foi ainda maior, foram produzidas 2 342 peças a mais que em janeiro. Quantas peças foram produzidas ao final dos dois meses?
a) 14 909
b) 16 753
c) 9 754
d) 27 476
e) 25 897
Habilidade da BNCC EF06MA03
Exercício 2 (múltiplos e divisores) - difícil
OBMEP
Uma turma tem 36 alunos e cada um deles tem um número de 1 a 36 na lista de chamada. Ontem, a professora chamou Lia ao quadro-negro e mais os outros seis alunos cujos números eram múltiplos do número de Lia. Qual foi o maior número chamado?
a)14
b)20
c)25
d)32
e)35
Habilidade da BNCC EF06MA06
Exercício 3 (potenciação) - difícil
O Xadrez é um jogo muito antigo e ainda assim, muito popular. Neste jogo as peças são movidas sobre um tabuleiro quadriculado onde cada quadrado é chamado de casa. Observe o seguinte tabuleiro, conte a quantidade total de casas e peças e, depois, assinale a opção que determina essas quantidades na forma de potências com base igual a 2.

Habilidade da BNCC EF06MA03
Aprenda mais sobre potenciação.
Exercício 4 (frações) - fácil
A turma de Carlos possui 28 alunos, dos quais 1/4 são meninas. Sabendo disso, qual das opções abaixo representa o número de meninos?
a) 8
b) 7
c) 14
d) 21
e) 18
Habilidade da BNCC EF06MA09
Exercício 5 (operações com frações) - difícil
Roberto adora pizza e como estava com muita fome, foi até uma pizzaria e decidiu que comeria um rodízio. Conforme o garçom passava ele foi pedindo as fatias e por fim, havia comido:
1/2 de pizza de queijo e presento
3/4 de pizza de margarita
2/8 de pizza de frango e catupiry
Ao total, a fração que representa a quantidade de pizzas que Roberto comeu, é:
a) 17/8
b) 16/8
c) 7/12
d) 12/8
e) 4/16
Habilidade da BNCC EF06MA10
Exercício 6 (operações com frações) - fácil
Em relação ao conjunto de blocos abaixo, assinale a alternativa que representa a soma das frações dos blocos amarelos mais os laranjas.

a) 2/16
b) 6/8
c) 8/8
d) 6/16
e) 8/16
Habilidade da BNCC EF06MA10
Exercício 7 (operações com frações) - difícil
Pedro vai aproveitar o feriado para visitar seus pais que moram em outra cidade. O percurso para chegar a seu destino é de 500 km. Como Pedro é um motorista precavido, antes de sair checa seu carro e verifica que o marcador do tanque de combustível está com o ponteiro em 1/4 do tanque. Seu automóvel percorre 10 km com 1 litro de combustível e a capacidade total do tanque é de 100 litros. Que fração do tanque deve ser reabastecido para Pedro chegar a casa de seus pais, sem novas paradas?
a) 1/2
b) 1/3
c) 1/4
d) 1/5
e) 1/8
Habilidade da BNCC EF06MA10
Veja mais sobre frações.
Exercício 8 (operações com números decimais) - médio
Alessandro saiu de casa e foi ao mercado a pedido de sua mãe para comprar algumas coisas. A mãe de Alessandro lhe deu uma nota de R$ 200,00 e uma lista com os seguintes itens: 3 kg de arroz, 2 kg de feijão, 2 kg de tomates e 3 kg de batatas. Por fim, pediu para que guardasse o troco e o devolve-se, pois ainda tinha outras despesas.
Veja os preços dos produtos:
1 kg de arroz, R$ 14,40
1 kg de feijão, R$ 7,30
1 kg de tomates, R$ 3,50
1 kg de batatas, R$ 4,75
Marque a opção que representa a quantia do troco que Alessandro devolveu para sua mãe.
a) R$ 118,35
b) R$ 120,95
c) R$ 90,25
d) R$ 85,75
e) R$ 135,35
Habilidade da BNCC EF06MA11
Exercício 9 (operações com números decimais) - fácil
Esta é a pirâmide da multiplicação, nela, o valor de um bloco acima é igual ao produto dos dois de baixo. Descubra e assinale a opção que representa o valor no bloco mais alto.

a) 506,25
b) 5,0625
c) 0,050625
d) 50,625
e) 0,50625
Habilidade da BNCC EF06MA11
Exercício 10 (operações com números decimais) - médio
Em uma loja de eletrodomésticos, uma geladeira era ofertada por R$ 2 300,00 à vista. No entanto, o cliente poderia optar por pagar a geladeira em 12 vezes de R$ 205,30. Marque a opção que indica a quantia final, caso escolhesse pagar à prestação, e, a diferença em relação ao preço à vista.
a) Preço à prestação R$ 2 363,60 e, a diferença com o preço à vista, R$ 63,60
b) Preço à prestação R$ 2 463,60 e, a diferença com o preço à vista, R$ 163,60
c) Preço à prestação R$ 2 563,60 e, a diferença com o preço à vista, R$ 263,60
d) Preço à prestação R$ 2 463,60 e, a diferença com o preço à vista, R$ 363,60
e) Preço à prestação R$ 2 463,60 e, a diferença com o preço à vista, R$ 463,60
Habilidade da BNCC EF06MA11
Exercício 11 (operações com números decimais) - fácil
Carla decidiu se dedicar mais a uma de suas atividades favoritas: a jardinagem. Ela que gosta de cultivar flores e aumentou a área do jardim. Para conseguir regar todas as mudas, ela comprou uma mangueira que é vendida por metro. Ela comprou 9 metros e pagou um total de R$ 70,65. Assinale a opção que representa o preço do metro da mangueira.
a) 6,54
b) 7,83
c) 8,45
d) 7,85
e) 9,81
Habilidade da BNCC EF06MA11
Estude sobre números decimais.
Exercício 12 (igualdades) - médio
A seguinte balança funciona através do equilíbrio entre os lados esquerdo e direito. Dizemos que a balança está equilibrada quando os dois lados estão a mesma altura e, para isso, as massas devem ser iguais dos dois lados. Diante disso, calcule o valor que está faltando e assinale a opção que representa a equação verdadeira.

a) 37kg + 14kg = 8kg + 43kg
b) 37kg + 15kg = 8kg + 43kg
c) 37kg + 24kg = 8kg + 43kg
d) 37kg + 9kg = 8kg + 43kg
e) 37kg + 18kg = 8kg + 43kg
Habilidades da BNCC EF06MA14, EF06MA03
Exercício 13 (medida de comprimento) - difícil
Entre os muitos esportes de corrida a maratona é muito popular. De acordo com a Federação Internacional de Atletismo, os atletas devem correr uma distância de 42 195 m. Outra modalidade, mais rápida, é a meia maratona, onde os atletas percorrem a metade desta distância. Assinale a opção que melhor aproxima a distância de uma meia maratona.
a) 210,97 km
b) 21097 hm
c) 21,097 km
d) 21097 km
e) 2109,7 km
Habilidades da BNCC EF06MA03, EF06MA24
Exercício 14 (perímetro) - fácil
Daniel está pensando em se mudar para o interior, fazer uma plantação de morangos orgânicos e criar galinhas. Para isso, está procurando por ofertas de chácaras. Depois de muito pesquisar, encontrou uma que parece ser interessante. Veja a planta baixa da propriedade e ajude Daniel a comprar sua propriedade marcando a opção que fornece o perímetro da chácara.

a) 185 m
b) 375 m
c) 285 m
d) 300 m
e) 385 m
Habilidade da BNCC EF06MA24
Aprenda mais sobre medidas de comprimento.
Exercício 15 (área) - fácil
OBMEP
Um dos retângulos abaixo tem área igual à área da figura ao lado.
Qual é esse retângulo?
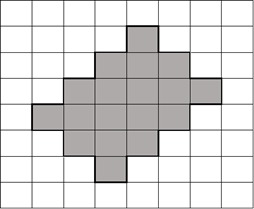
a) 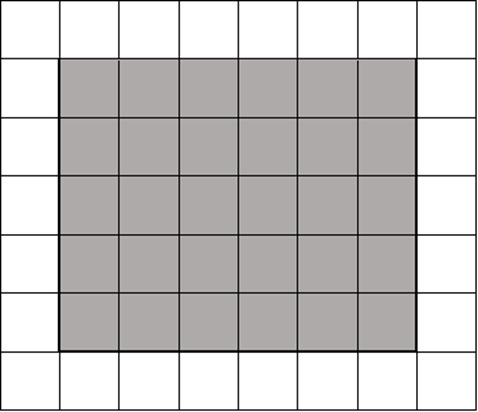
b) 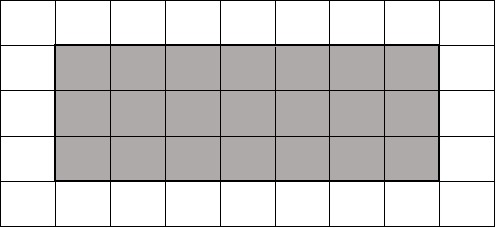
c) 
d) 
e) 
Habilidade da BNCC EF06MA24
Exercício 16 (área) - médio
Joana irá fazer uma reforma na sala de sua casa. Em uma das paredes decidiu colocar um painel com placas de revestimento. Cada placa possui 125 cm de largura por 50 cm de altura. O painel terá 5 placas na largura e 4 placas na altura. Senda assim, assinale a opção da área total coberta pelo painel.
Habilidade da BNCC EF06MA24
Exercício 17 (medida de tempo) - fácil
Um cinema foi recentemente inaugurado próximo à praça da cidade. Como o movimento aos finais de semana aumenta e muitas pessoas passam por ali, ao observar a situação, Luís decidiu fazer um empreendimento e montou um carrinho de vender pipocas. Para ter uma previsão aproximada das vendas, Luís fez uma média da quantidade de saquinhos de pipoca vendidos por minuto, encontrando a quantia de 1 saquinho vendido a cada 2 minutos.
Considerando um dia de 8h trabalhadas, marque a opção que representa a quantidade de saquinhos de pipoca vendidos no dia.
a) 210
b) 200
c) 320
d) 240
e) 170
Habilidade BNCC EF06MA24
Exercício 18 (volume) - fácil
Analise os sólidos abaixo e indique a opção que apresenta, respectivamente, os volumes dos sólidos A e B.


a) A, 36 cubos e B, 43 cubos
b) A, 48 cubos e B, 54 cubos
c) A, 48 cubos e B, 53 cubos
d) A, 36 cubos e B, 48 cubos
e) A, 48 cubos e B, 42 cubos
Habilidade da BNCC EF06MA24
Veja sobre volume.
Exercício 19 (poliedros) - fácil
Um poliedro é uma figura espacial com lados planos, ou seja, não arredondados. Analise a figura abaixo e assinale a afirmativa que indica o número de faces, vértices e arestas.

a) 5 faces, 5 vértices, 9 arestas
b) 4 faces, 5 vértices, 7 arestas
c) 4 faces, 6 vértices, 8 arestas
d) 5 faces, 5 vértices, 8 arestas
e) 5 faces, 8 vértices, 10 arestas
Habilidade BNCC EF06MA17
Exercício 20 (sólidos geométricos) - médio
Em relação aos prismas e pirâmides, marque a opção falsa.
a) Ambos são poliedros.
b) Em uma pirâmide de base triangular e um prisma de base triangular, o prisma possui um número maior de arestas.
c) Nas pirâmides, existe uma base e, dela saem arestas que se encontram em um único vértice, fora da base.
d) Ambos possuem duas bases iguais.
e) Nos prismas, as duas bases, são formadas por polígonos iguais.
Habilidade da BNCC EF06MA17
Exercício 21 (sólidos geométricos) - médio
Em relação aos sólidos geométricos, assinale a afirmativa verdadeira.
a) Pirâmide não é um poliedro.
b) O cone é um poliedro.
c) O cubo é um poliedro com todos os lados iguais.
d) Prismas são figuras com duas bases diferentes.
e) Uma pirâmide de base triangular possui 5 arestas.
Habilidade da BNCC EF06MA17
Estude poliedros.
Exercício 22 (polígonos) - fácil
Na figura abaixo, há seis figuras planas. Qual das opções, em ordem crescente, as classifica corretamente em polígonos e não polígonos?

a) Não polígono, polígono, não polígono, polígono, não polígono, não polígono.
b) Não polígono, não polígono, não polígono, polígono, não polígono, não polígono.
c) Não polígono, não polígono, não polígono, polígono, não polígono, polígono.
d) Não polígono, polígono, não polígono, polígono, polígono, polígono.
e) Não polígono, polígono, não polígono, polígono, polígono, não polígono.
Habilidade da BNCC EF06MA18
Exercício 23 (ângulos) - fácil
ENEM 2017
A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, que foi colocada em uma parede para exposição e fixada nos pontos A e B.
Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.
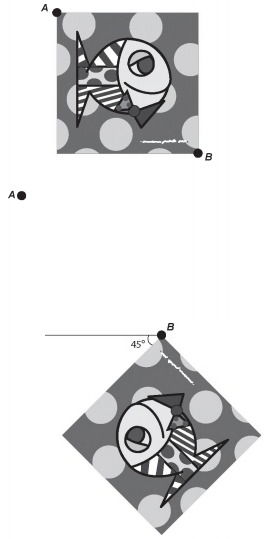
Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360°. A forma de recolocar a tela na posição original, obedecendo ao que foi estabelecido, é girando-a em um ângulo de:
a) 90º no sentido horário.
b) 135º no sentido horário.
c) 180º no sentido anti-horário.
d) 270º no sentido anti-horário.
e) 315º no sentido horário.
Habilidade da BNCC EF06MA18
Exercício 24 (ângulos) - fácil
Veja também Planos de aula de Matemática para o 6º ano do EF.
Aprenda mais com
- 23 exercícios de Matemática 7º ano
- 27 exercícios de Matemática Básica
- Exercícios de Matemática 8º ano
- Exercícios de Matemática 9º ano com respostas
- Como calcular porcentagem
- Exercícios sobre ângulos respondidos
- Subtração
- Potência com expoente fracionário
- Atividades de multiplicação para 6º ano
- Atividades sobre antecessor e sucessor (Matemática | 1º ano do Fundamental)
ASTH, Rafael. Atividades de Matemática do 6º ano (com questões resolvidas). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-matematica-6-ano/. Acesso em:





