Princípio fundamental da contagem

O princípio fundamental da contagem, também chamado de princípio multiplicativo, é utilizado para encontrar o número de possibilidades para um evento constituído de n etapas. Para isso, as etapas devem ser sucessivas e independentes.

Se a primeira etapa do evento possui x possibilidades e a segunda etapa é constituída de y possibilidades, então existem x . y possibilidades.

Portanto, o princípio fundamental da contagem é a multiplicação das opções dadas para determinar o total de possibilidades.

Esse conceito é importante para a análise combinatória, área da Matemática que reúne os métodos para resolução de problemas que envolvem a contagem e, por isso, é muito útil na investigação de possibilidades para determinar a probabilidade de fenômenos.

Exemplo 1

João está em um hotel e pretende ir visitar o centro histórico da cidade. Partindo do hotel existem 3 linhas de metrô que levam ao shopping e 4 ônibus que se deslocam do shopping para o centro histórico.

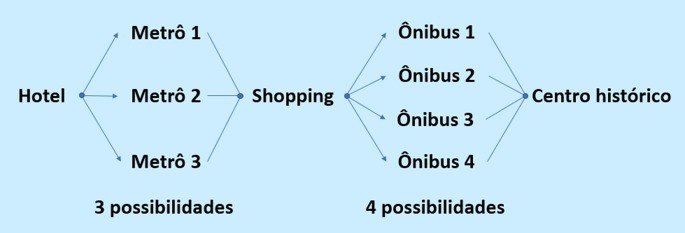
De quantas maneiras João pode sair do hotel e chegar até o centro histórico passando pelo shopping?

Solução: O diagrama de árvore ou árvore de possibilidades é útil para analisar a estrutura de um problema e visualizar o número de combinações.

Observe como a constatação das combinações foi feita utilizando o diagrama de árvore.

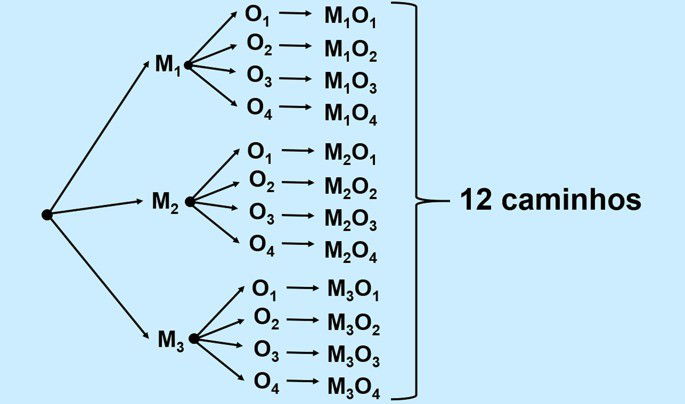
Se existem 3 possibilidades de sair do hotel e chegar até o shopping, e do shopping para o centro histórico temos 4 possibilidades, então o total de possibilidades é 12.

Outra maneira de resolver o exemplo seria pelo princípio fundamental da contagem, efetuando a multiplicação das possibilidades, ou seja, 3 x 4 = 12.

Exemplo 2

Um restaurante possui em seu cardápio 2 tipos de entradas, 3 tipos de pratos principais e 2 tipos de sobremesas. Quantos menus poderiam ser montados para uma refeição com uma entrada, um prato principal e uma sobremesa?

Solução: Utilizaremos a árvore de possibilidades para entender a montagem dos menus com entrada (E), prato principal (P) e sobremesa (S).

Pelo princípio fundamental da contagem, temos: 2 x 3 x 2 = 12. Portanto, poderiam ser formados 12 menus com uma entrada, um prato principal e uma sobremesa.

Exercícios de princípio fundamental da contagem resolvidos

Questão 1

Ana estava se organizando para viajar e colocou na mala 3 calças, 4 blusas e 2 sapatos. Quantas combinações Ana pode formar com uma calça, uma blusa e um sapato?

a) 12 combinações
b) 32 combinações
c) 24 combinações
d) 16 combinações

Questão 2

Um professor elaborou uma prova com 5 questões e os alunos deveriam respondê-la assinalando verdadeiro (V) ou falso (F) para cada uma das questões. De quantas maneiras distintas o teste poderia ser respondido?

a) 25
b) 40
c) 24
d) 32

Questão 3

De quantas maneiras um número com 3 algarismos distintos pode ser formado utilizando 0, 1, 2, 3, 4 e 5?

a) 200
b) 150
c) 250
d) 100

Adquira mais conhecimento com os textos a seguir:

• Combinação na matemática: como calcular e exemplos
• Análise Combinatória
• Permutação
• Arranjo na matemática: o que é, como calcular, exemplos
• Fatorial
• Probabilidade

Comece a praticar com:

• Exercícios de Análise Combinatória
• Exercícios de Probabilidade
• Exercícios sobre princípio fundamental da contagem