Permutação: simples e com repetição

Rafael C. Asth

Professor de Matemática e Física

A permutação é uma técnica de contagem utilizada para determinar quantas maneiras existem para ordenar os elementos de um conjunto finito. Fazer uma permuta é realizar uma troca e, nos problemas de combinatória, significa trocar os elementos de lugar, considerando a ordenação desses.

Essas técnicas fazem parte de um campo da Matemática chamado, Análise Combinatória, que se destina a conhecer e contar os diferentes modos de organizar conjuntos e seus elementos. A permutação simples e a com elementos repetidos tratam desta categoria de problemas.

Permutação simples

Uma permutação simples é a ordenação dos elementos de um conjunto finito, quando seus elementos não se repetem, são distintos. É utilizada para determinar a quantidade dessas ordenações.

A quantidade $P com n subscrito$ de permutações de um conjunto de n elementos é igual a n! (lê-se n fatorial).

A fórmula para determinar a quantidade de permutações simples é

$começar estilo tamanho matemático 18px reto P com reto n subscrito espaço igual a espaço reto n fatorial fim do estilo$

Considere um conjunto com n elementos. Para organizá-los em uma fila, precisamos escolher o primeiro e, para isso, temos n possibilidades. Para escolher o segundo, temos (n-1) possibilidades, uma menos, pois, já usamos uma opção ao escolher o primeiro. Esse processo continua até que só reste um elemento.

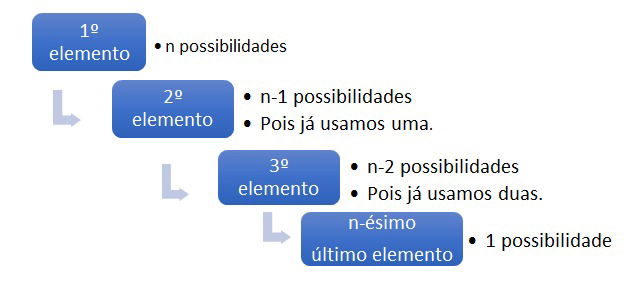
Ordem dos elementos e suas possibilidades. — Ordens dos elementos e suas possibilidades.

Para determinar a quantidade total de permutações, multiplicamos a quantidade de possibilidades existentes na escolha de cada elemento. Dessa forma:

$n sinal de multiplicação parêntese esquerdo n menos 1 parêntese direito sinal de multiplicação parêntese esquerdo n menos 2 parêntese direito sinal de multiplicação espaço reticências horizontais espaço sinal de multiplicação 3 espaço x espaço 2 espaço x espaço 1$

A expressão acima é chamada fatorial de n e usamos o símbolo n!.

Aprenda mais sobre fatorial .

Exemplo
Os diferentes modos de organizar as letras de uma palavra são chamados de anagramas. Quantos anagramas existem para a palavra PATO?

Essas são as possibilidades:

Assim, como a palavra PATO possui 4 letras, temos que

$P com 4 subscrito espaço igual a espaço 4 fatorial espaço igual a espaço 4 espaço x espaço 3 espaço x espaço 2 espaço x espaço 1 espaço igual a espaço 24$

Portanto, há 24 permutações simples para a palavra PATO.

Permutação com repetição

Uma permutação com elementos repetidos acontece quando em um conjunto de n elementos, alguns destes são iguais.

Na fórmula para determinar o número de permutações com repetição, dividimos o fatorial do número total n de elementos, pelo produto entre os fatoriais dos elementos que se repetem.

$P com n subscrito com parêntese esquerdo a vírgula espaço b vírgula espaço c vírgula espaço reticências horizontais parêntese direito sobrescrito fim do sobrescrito espaço igual a numerador n fatorial sobre denominador a fatorial sinal de multiplicação b fatorial sinal de multiplicação c fatorial fim da fração$

$P com n subscrito$ é o número de permutações de n elementos.

$a vírgula espaço b vírgula espaço c vírgula espaço reticências horizontais$ são os números de elementos de cada tipo que se repetem.

$n fatorial$ é o fatorial do número total de elementos n.

Exemplo

Vamos determinar quantas permutações existem para a palavra OVO. Para facilitar vamos colorir as letras. Vejamos os anagramas da palavra OVO.

$Na espaço prática espaço as espaço seguintes espaço permutações espaço equivalem espaço reto a espaço apenas espaço uma. reto O reto V reto O reto O reto V reto O espaço Assim espaço como reto O reto O reto V reto O reto O reto V Também espaço com espaço reto V reto O reto O reto V reto O reto O$

O número de permutações simples com 3 elementos é dada por

$P com 3 subscrito espaço igual a espaço 3 fatorial espaço igual a espaço 3 espaço x espaço 2 espaço x espaço 1 espaço igual a espaço 6$

No entanto, algumas permutações se repetem e não podemos contá-las duas vezes. Para isso devemos dividir o valor de $P com 3 subscrito$ (pois a palavra possui três letras), por $P com 2 subscrito$ (pois a letra O se repete duas vezes).

$P com n subscrito espaço igual a espaço numerador 3 fatorial sobre denominador 2 fatorial fim da fração espaço igual a espaço numerador 3 sinal de multiplicação 2 sinal de multiplicação 1 sobre denominador 2 sinal de multiplicação 1 fim da fração espaço igual a espaço 6 sobre 2 espaço igual a espaço 3$

Dessa forma, o número de permutações para as letras da palavra OVO é igual a 3.

Vejamos este outro exemplo em que definiremos o número de permutações para as letras da palavra BANANA.

$P com 6 subscrito com parêntese esquerdo A vírgula N parêntese direito sobrescrito fim do sobrescrito igual a numerador 6 fatorial sobre denominador 3 fatorial sinal de multiplicação 2 fatorial fim da fração$

Onde:

$P com 6 subscrito com parêntese esquerdo A vírgula N parêntese direito sobrescrito fim do sobrescrito$ significa permutação com 6 elementos onde as letras A e N se repetem.

3! pois, a letra A se repete três vezes.

2! pois, a letra N se repete duas vezes.

Uma dica para facilitar o cálculo é desenvolver o 6! até chegar em 3!, fazendo a simplificação com o denominador. Veja o desenvolvimento.

$P com 6 subscrito com parêntese esquerdo A vírgula N parêntese direito sobrescrito fim do sobrescrito espaço igual a numerador 6 sinal de multiplicação 5 sinal de multiplicação 4 sinal de multiplicação 3 fatorial sobre denominador 3 fatorial sinal de multiplicação 2 fatorial fim da fração espaço texto cortando o 3! fim do texto P com 6 subscrito com parêntese esquerdo A vírgula N parêntese direito espaço sobrescrito fim do sobrescrito igual a numerador 6 sinal de multiplicação 5 sinal de multiplicação 4 sobre denominador 2 sinal de multiplicação 1 fim da fração espaço igual a espaço 120 sobre 2 espaço igual a espaço 60 espaço$

Sendo assim, o número de permutações para as letras da palavra BANANA é igual a 60.

Exercícios de permutação

Questão 1

Calcule o valor de $P com 7 subscrito$ .

Ver Resposta

$P com 7 subscrito espaço igual a espaço 7 fatorial espaço igual a espaço 7 sinal de multiplicação 6 sinal de multiplicação 5 sinal de multiplicação 4 sinal de multiplicação 3 sinal de multiplicação 2 sinal de multiplicação 1 espaço igual a espaço 5040$

Questão 2

Considere uma fila de pessoas organizadas por ordem de chegada em que, em um determinado momento, há seis pessoas. De quantas formas diferentes essas pessoas poderiam estar ordenadas do primeiro ao último lugar?

Ver Resposta

Cada forma de ordenação é uma permutação simples, uma vez que os indivíduos são únicos e não se repetem. Dessa forma, havendo seis pessoas, a resposta é uma permutação com 6 elementos.

$P com 6 subscrito espaço igual a espaço 6 sinal de multiplicação 5 sinal de multiplicação 4 sinal de multiplicação 3 sinal de multiplicação 2 sinal de multiplicação 1 espaço igual a espaço 720$

Questão 3

Considere a palavra GARFO e responda as seguintes questões?

a) Quantos são os anagramas da palavra GARFO?

Ver Resposta

Como as letras não se repetem esse é um caso de permutação simples de 5 elementos.

$reto P com 5 subscrito igual a 5 sinal de multiplicação 4 sinal de multiplicação 3 sinal de multiplicação 2 sinal de multiplicação 1 espaço igual a espaço 120$

b) Quantos são os anagramas que começam com a letra A?

Ver Resposta

Nesse caso, fixamos a letra A no início e calculamos as permutações com as letras GRFO, que são permutações de 4 elementos.

1 possibilidade para a letra A x $P com 4 subscrito espaço igual a espaço 4 sinal de multiplicação 3 sinal de multiplicação 2 sinal de multiplicação 1 espaço igual a espaço 24$

c) Quantos são os anagramas no caso das vogais estarem sempre uma ao lado da outra?

Ver Resposta

Uma possibilidade seria G R F A O.

Consideramos AO como uma letra e fazemos fatorial de 4. P4 = 4 x 3 x 2 x 1 = 24.

Depois multiplicamos por 2 fatorial, pois há AO e OA.

P2 = 2 x 1 = 2

Portanto, existem 48 anagramas no caso em que as vogais estão sempre juntas.

Pratique mais exercícios de permutação.

Talvez se interesse por estes conteúdos sobre Análise Combinatória:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações