Análise Combinatória

A análise combinatória ou combinatória é a parte da Matemática que estuda métodos e técnicas que permitem resolver problemas relacionados com contagem.

Muito utilizada nos estudos sobre probabilidade, ela faz a análise das possibilidades e das combinações possíveis entre um conjunto de elementos.

Princípio Fundamental da Contagem

O princípio fundamental da contagem, também chamado de princípio multiplicativo, postula que:

Quando um evento é composto por n etapas sucessivas e independentes, de tal modo que as possibilidades da primeira etapa é x e as possibilidades da segunda etapa é y, resulta no número total de possibilidades de o evento ocorrer, dado pelo produto (x) . (y).

Em resumo, no princípio fundamental da contagem, multiplica-se o número de opções entre as escolhas que lhe são apresentadas.

Exemplo

Uma lanchonete vende uma promoção de lanche a um preço único. No lanche, estão incluídos um sanduíche, uma bebida e uma sobremesa. São oferecidas três opções de sanduíches: hambúrguer especial, sanduíche vegetariano e cachorro-quente completo. Como opção de bebida, pode-se escolher 2 tipos: suco de maçã ou guaraná. Para a sobremesa, existem quatro opções: cupcake de cereja, cupcake de chocolate, cupcake de morango e cupcake de baunilha. Considerando todas as opções oferecidas, de quantas maneiras um cliente pode escolher o seu lanche?

Solução

Podemos começar a resolução do problema apresentado construindo uma árvore de possibilidades, conforme ilustrado abaixo:

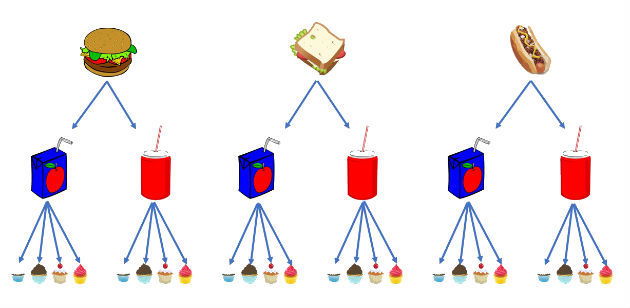
Acompanhando o diagrama, podemos diretamente contar quantos tipos diferentes de lanches podemos escolher. Assim, identificamos que existem 24 combinações possíveis.

Podemos ainda resolver o problema usando o princípio multiplicativo. Para determinar as diferentes possibilidades de lanches, basta multiplicar o número de opções de sanduíches, bebidas e sobremesa.

Total de possibilidades: 3.2.4 = 24

Portanto, temos 24 tipos diferentes de lanches para escolher na promoção.

Aprenda mais sobre princípio fundamental da contagem.

Tipos de Combinatória

O princípio fundamental da contagem pode ser usado na maioria dos problemas relacionados com contagem. Entretanto, em algumas situações seu uso torna a resolução muito trabalhosa.

Desta maneira, usamos algumas técnicas para resolver problemas com determinadas características. Basicamente há três tipos de agrupamentos: arranjos, combinações e permutações.

Antes de conhecermos melhor esses procedimentos de cálculo, precisamos definir uma ferramenta muito utilizada em problemas de contagem, o fatorial.

O fatorial de um número natural é definido como o produto deste número por todos os seus antecessores. Utilizamos o símbolo para indicar o fatorial de um número.

Define-se ainda que o fatorial de zero é igual a 1.

Exemplo

O! = 1
1! = 1
3! = 3.2.1 = 6
7! = 7.6.5.4.3.2.1 = 5 040
10! = 10.9.8.7.6.5.4.3.2.1 = 3 628 800

Note que o valor do fatorial cresce rapidamente, conforme cresce o número. Então, frequentemente usamos simplificações para efetuar os cálculos de análise combinatória.

Saiba mais sobre fatorial.

Arranjos

Nos arranjos, os agrupamentos dos elementos dependem da ordem e da natureza dos mesmos.

Para obter o arranjo simples de n elementos tomados, p a p (p ≤ n), utiliza-se a seguinte expressão:

Exemplo

Como exemplo de arranjo, podemos pensar na votação para escolher um representante e um vice-representante de uma turma, com 20 alunos. Sendo que o mais votado será o representante e o segundo mais votado o vice-representante.

Dessa forma, de quantas maneiras distintas a escolha poderá ser feita? Observe que nesse caso, a ordem é importante, visto que altera o resultado.

Logo, o arranjo pode ser feito de 380 maneiras diferentes.

Permutações

As permutações são agrupamentos ordenados, onde o número de elementos (n) do agrupamento é igual ao número de elementos disponíveis.

Note que a permutação é um caso especial de arranjo, quando o número de elementos é igual ao número de agrupamentos. Desta maneira, o denominador na fórmula do arranjo é igual a 1 na permutação.

Assim a permutação é expressa pela fórmula:

Exemplo

Para exemplificar, vamos pensar de quantas maneiras diferentes 6 pessoas podem se sentar em um banco com 6 lugares.

Como a ordem em que irão se sentar é importante e o número de lugares é igual ao número de pessoas, iremos usar a permutação:

Logo, existem 720 maneiras diferentes para as 6 pessoas sentarem neste banco.

Combinações

As combinações são subconjuntos onde a ordem dos elementos não é importante, entretanto, são caracterizadas pela natureza dos mesmos.

Assim, para calcular uma combinação simples de n elementos tomados p a p (p ≤ n), utiliza-se a seguinte expressão:

Exemplo

A fim de exemplificar, podemos pensar na escolha de 3 membros para formar uma comissão organizadora de um evento, dentre as 10 pessoas que se candidataram.

De quantas maneiras distintas essa comissão poderá ser formada?

Note que, ao contrário dos arranjos, nas combinações a ordem dos elementos não é relevante. Isso quer dizer que escolher: Maria, João e José, é equivalente a escolher: João, José e Maria.

Observe que para simplificar os cálculos, transformamos o fatorial de 10 em produto, mas conservamos o fatorial de 7, pois, desta forma, foi possível simplificar com o fatorial de 7 do denominador.

Assim, existem 120 maneiras distintas formar a comissão.

Aprenda mais sobre combinação.

Probabilidade e Análise Combinatória

A probabilidade permite analisar ou calcular as chances de obter determinado resultado diante de um experimento aleatório. São exemplos as chances de um determinado número sair em um lançamento de dados, ou, a possibilidade de ganhar na loteria.

A partir disso, a probabilidade é determinada pela razão entre o número de casos favoráveis e número de casos possíveis, apresentada pela seguinte expressão:

Sendo:

P (A): probabilidade de ocorrer um evento A;
n (A): número de resultados favoráveis
n (Ω): número total de resultados possíveis

Para encontrar o número de casos possíveis e favoráveis, muitas vezes necessitamos recorrer às fórmulas estudadas em análise combinatória.

Exemplo

Qual a probabilidade de um apostador ganhar o prêmio máximo da mega-sena, fazendo uma aposta mínima, ou seja, apostar exatamente nos seis números sorteados?

Solução

Como vimos, a probabilidade é calculada pela razão entre os casos favoráveis e os casos possíveis. Nesta situação, temos apenas um caso favorável, ou seja, apostar exatamente nos seis números sorteados.

Já o número de casos possíveis é calculado considerando que serão sorteados, ao acaso, 6 números, não importando a ordem, de um total de 60 números.

Para fazer esse cálculo, usaremos a fórmula de combinação, conforme indicado abaixo:

Assim, existem 50 063 860 modos distintos de sair o resultado. A probabilidade de acertarmos então será calculada como:

Veja mais sobre Probabilidade.

Exercícios de análise combinatória com gabarito

Exercício 1

Uma pessoa mora na cidade A e deseja viajar para conhecer a cidade C. Para isso, é preciso passar primeiro pela cidade B. Existem 4 caminhos que levam até a cidade B e, a partir da cidade B, três caminhos que levam até a cidade C. Supondo que a única maneira de chegar até a cidade C seja passando por B, de quantas formas diferentes esta pessoa pode ir até à cidade C, e voltar para cidade A?

Exercício 2

Gabriel, Maurício, Luiza, Paula e Raquel são um grupo de amigos que decidem ir ao cinema. Eles compram ingressos na mesma fileira, de forma que estejam sempre juntos, sem nenhuma cadeira vazia ou ocupada por outro espectador. Como Maurício e Luiza são namorados, eles irão sentar lado a lado. De quantas maneiras o grupo de amigos podem se sentar, de modo que o casal permaneça junto?

Exercício 3

Um restaurante oferece oito opções para montar sua refeição, dentre as quais, o cliente pode escolher 4 destas para cada prato. Suponha que um cliente almoçará todos os dias neste restaurante, enquanto houver opções diferentes. Quantos dias este cliente poderá almoçar no restaurante, sem repetir uma refeição?

Para completar seus estudos faça os Exercícios de Análise Combinatória

Leia também:

• Estatística
• Permutação
• Arranjo na matemática: o que é, como calcular, exemplos
• Probabilidade Condicional
• Exercícios de Probabilidade (fáceis)
• Exercícios de Probabilidade
• Binômio de Newton