Probabilidade Condicional

Rafael C. Asth

Professor de Matemática e Física

Probabilidade condicional ou probabilidade condicionada é um conceito da matemática que envolve dois eventos (A e B) de um mesmo espaço amostral (S) finito e não vazio.

A probabilidade condicional considera que, ocorrido um evento, este influencia a ocorrência do outro, ou seja, são eventos dependentes.

A probabilidade condicional do evento A ocorrer, tendo ocorrido B é:

$começar estilo tamanho matemático 18px reto P parêntese esquerdo reto A dividido por reto B parêntese direito igual a numerador reto P parêntese esquerdo reto A intersecção reto B parêntese direito sobre denominador reto P parêntese esquerdo reto B parêntese direito fim da fração fim do estilo$

Onde,
$reto P parêntese esquerdo reto A intersecção reto B parêntese direito espaço$ é a probabilidade da interseção entre A e B.
$reto P parêntese esquerdo reto B parêntese direito$ é a probabilidade do evento B.

Analogamente, a probabilidade de ocorrer B, tendo ocorrido A é:

$Error converting from MathML to accessible text.$

Probabilidade, espaço amostral e eventos

O “espaço amostral” é o conjunto de resultados possíveis obtidos a partir de um fenômeno aleatório. Já os subconjuntos de um espaço amostral são denominados “eventos”.

Sendo assim, temos que a probabilidade é calculada pela divisão de um evento, pelo espaço amostral.

$reto P parêntese esquerdo reto A parêntese direito igual a numerador reto n parêntese esquerdo reto A parêntese direito sobre denominador reto n parêntese esquerdo reto ómega maiúsculo parêntese direito fim da fração$

Onde,

P(A): probabilidade de ocorrência do evento A,
n(A): número de casos favoráveis ao evento A,
n $reto ómega maiúsculo$ : número total de casos possíveis

Exemplo
Supomos que um avião com 140 passageiros saia de São Paulo com destino à Bahia. Durante esse voo, os passageiros responderam duas questões (eventos):

Já viajou de avião antes? (primeiro evento)
Já esteve na Bahia? (segundo evento)

Eventos	Passageiros viajando de avião pela primeira vez	Passageiros que já tinham viajado de avião	Total
Passageiros que não conheciam a Bahia	85	25	110
Passageiros que já conheciam a Bahia	20	10	30
Total	105	35	140

A partir disso, um passageiro que viaja pela primeira vez de avião é escolhido. Nesse caso, qual seria a probabilidade desse mesmo passageiro já conhecer a Bahia?

n(viajando de avião pela primeira vez) = 105
n(viajando de avião pela primeira vez e já conhecer a Bahia) = 20

Note que esse número corresponde à probabilidade do passageiro escolhido já conhecer a Bahia, enquanto viajava de avião pela primeira vez.

Assim, segundo a tabela acima podemos concluir que:

20 é o número de passageiros que já estiveram na Bahia E estão viajando a primeira vez de avião;
105 é o número total dos passageiros que já viajaram de avião.

A probabilidade condicional é indicada por:

$negrito P negrito espaço negrito parêntese esquerdo negrito já negrito espaço negrito conhece negrito espaço negrito a negrito espaço negrito Bahia negrito espaço negrito dividido por negrito espaço negrito primeira negrito espaço negrito vez negrito espaço negrito que negrito espaço negrito viaja negrito espaço negrito de negrito espaço negrito avião negrito parêntese direito negrito espaço igual a espaço numerador parêntese esquerdo já espaço conhece espaço reto a espaço Bahia espaço intersecção espaço primeira espaço vez espaço que espaço viaja espaço de espaço avião parêntese direito sobre denominador espaço parêntese esquerdo primeira espaço vez espaço que espaço viaja espaço de espaço avião parêntese direito fim da fração igual a 20 sobre 105$

Perceba que o conector E tem o significado de interseção.

Assim, temos que os eventos A e B de um espaço amostral finito e não vazio (Ω) podem ser expressos por:

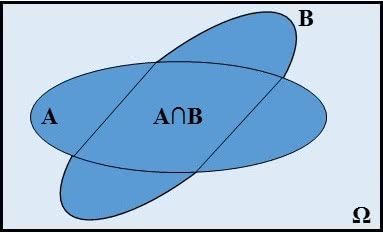
Exercícios de probabilidade condicional

Exercício 1

(UFSCAR) Dois dados usuais e não viciados são lançados. Sabe-se que os números observados são ímpares. Então, a probabilidade de que a soma deles seja 8 é:

a) 2/36
b) 1/6
c) 2/9
d) 1/4
e) 2/18

Ver Resposta

Resposta correta: c) 2/9

Objetivo: uma vez que os resultados foram ímpares, determinar a probabilidade da soma ser 8.

Resolução
Sair soma 8 é um evento condicionado por sair resultados ímpares nos dois dados.

Sejam os eventos:
A, resultados ímpares
B, soma 8

A probabilidade condicional de sair soma 8, tendo saído resultados ímpares, é:

A quantidade total de duplas de resultados é 36, pois 6 x 6 = 36.

A quantidade de apenas resultados ímpares é 9, sendo:

1 e 1; 1 e 3; 1 e 5
3 e 1; 3 e 3; 3 e 5
5 e 1; 5 e 3; 5 e 5

$p parêntese esquerdo A parêntese direito igual a 9 sobre 36$

Destes, as somas 8 são 3 + 5 = 5 + 3 = 8

$P parêntese esquerdo A intersecção B parêntese direito igual a 2 sobre 36$

Substituindo na fórmula da probabilidade condicional:

$P parêntese esquerdo B dividido por A parêntese direito igual a numerador p parêntese esquerdo A intersecção B parêntese direito sobre denominador p parêntese esquerdo A parêntese direito fim da fração igual a numerador começar estilo mostrar numerador 9 sobre denominador diagonal para cima risco 36 fim da fração fim do estilo sobre denominador começar estilo mostrar numerador 2 sobre denominador diagonal para cima risco 36 fim da fração fim do estilo fim da fração igual a 2 sobre 9$

Exercício 2

(Enem-2012) Em um blog de variedades, músicas, mantras e informações diversas, foram postados “Contos de Halloween”. Após a leitura, os visitantes poderiam opinar, assinalando suas reações em: “Divertido”, “Assustador” ou “Chato”. Ao final de uma semana, o blog registrou que 500 visitantes distintos acessaram esta postagem.

O gráfico a seguir apresenta o resultado da enquete.

O administrador do blog irá sortear um livro entre os visitantes que opinaram na postagem “Contos de Halloween”.

Sabendo que nenhum visitante votou mais de uma vez, a probabilidade de uma pessoa escolhida ao acaso entre as que opinaram ter assinalado que o conto “Contos de Halloween” é “Chato” é mais aproximada por:

a) 0,09
b) 0,12
c) 0,14
d) 0,15
e) 0,18

Ver Resposta

Resposta correta: d)0,15

Objetivo: probabilidade de que, entre as que opinaram, ser sorteada uma pessoa que assinalou chato.

Sendo os eventos:

A: opinou
B: assinalou chato

A probabilidade de ser sorteada uma pessoa que assinalou chato, dentre as que as que opinaram é:

Probabilidade de ser alguém que sorteou P(A):

79% das 500 opinaram. Veja que 21% não opinou.

$79 sinal de percentagem espaço d e espaço 500 espaço igual a 79 sobre 100 sinal de multiplicação 500 espaço igual a espaço 395$

Sendo assim, $P parêntese esquerdo A parêntese direito igual a 395 sobre 500$

Probabilidade de ter opinado e assinalar chato $P parêntese esquerdo A intersecção B parêntese direito$ :

Veja que, de fato, 12% de 500 assinalaram chato, logo:

$12 sinal de percentagem espaço d e espaço 500 espaço igual a espaço 12 sobre 100 sinal de multiplicação 500 igual a 60$

Substituindo na fórmula da probabilidade condicional:

$P parêntese esquerdo B dividido por A parêntese direito igual a numerador P parêntese esquerdo A intersecção B parêntese direito sobre denominador P parêntese esquerdo A parêntese direito fim da fração igual a numerador começar estilo mostrar 395 sobre 500 fim do estilo sobre denominador começar estilo mostrar 60 sobre 500 fim do estilo fim da fração igual a 60 sobre 395 aproximadamente igual 0 vírgula 15$