Triângulo de Pascal

Rosimar Gouveia

Professora de Matemática e Física

Triângulo de Pascal é um triângulo aritmético infinito onde são dispostos os coeficientes das expansões binominais. Os números que compõem o triângulo apresentam diversas propriedades e relações.

Essa representação geométrica foi estudada pelo matemático chinês Yang Hui (1238-1298) e por muitos outros matemáticos.

Entretanto, os estudos mais famosos foram do matemático italiano Niccolò Fontana Tartaglia (1499-1559) e do matemático francês Blaise Pascal (1623-1662).

Sendo que Pascal estudou mais profundamente o triângulo aritmético e provou várias de suas propriedades.

Na antiguidade, esse triângulo era usado para o cálculo de algumas raízes. Mais recentemente, ele é utilizado no cálculo de probabilidades.

Além disso, os termos do binômio de Newton e da sequência de Fibonacci podem ser encontrados a partir dos números que constituem o triângulo.

Coeficiente Binomial

Os números que compõem o triângulo de Pascal são chamados de números binomiais ou coeficientes binomiais. Um número binomial é representado por:

$abre parênteses tabela linha com n linha com p fim da tabela fecha parênteses$

Com n e p números naturais e n ≥ p. O número n é denominado numerador e o p denominador.

O número binomial é calculado a partir da relação:

$abre parênteses tabela linha com n linha com p fim da tabela fecha parênteses igual a C com n vírgula p subscrito fim do subscrito igual a numerador n fatorial sobre denominador p fatorial parêntese esquerdo n menos p parêntese direito fatorial fim da fração$

Sendo,

C_n,p: combinação simples de n elementos tomados p a p
n!: fatorial de n, ou seja, n.(n - 1).(n - 2)...3.2.1
p!: fatorial de p, ou seja, p.(p - 1).(p - 2)...3.2.1

Construção do Triângulo

O triângulo de Pascal é construído colocando-se os números binomiais de mesmo numerador na mesma linha e os coeficientes de mesmo denominador na mesma coluna. Assim, temos:

$l i n h a espaço 0 espaço espaço espaço espaço espaço espaço espaço abre parênteses tabela linha com 0 linha com 0 fim da tabela fecha parênteses l i n h a espaço 1 espaço espaço espaço espaço espaço espaço espaço abre parênteses tabela linha com 1 linha com 0 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 1 linha com 1 fim da tabela fecha parênteses l i n h a espaço 2 espaço espaço espaço espaço espaço espaço espaço abre parênteses tabela linha com 2 linha com 0 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 2 linha com 1 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 2 linha com 2 fim da tabela fecha parênteses l i n h a espaço 3 espaço espaço espaço espaço espaço espaço espaço abre parênteses tabela linha com 3 linha com 0 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 3 linha com 1 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 3 linha com 2 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 3 linha com 3 fim da tabela fecha parênteses espaço l i n h a espaço 4 espaço espaço espaço espaço espaço espaço espaço abre parênteses tabela linha com 4 linha com 0 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 4 linha com 1 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 4 linha com 2 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 4 linha com 3 fim da tabela fecha parênteses espaço abre parênteses tabela linha com 4 linha com 4 fim da tabela fecha parênteses espaço espaço espaço espaço reticências verticais l i n h a espaço n espaço espaço espaço espaço espaço espaço espaço espaço abre parênteses tabela linha com n linha com 0 fim da tabela fecha parênteses espaço abre parênteses tabela linha com n linha com 1 fim da tabela fecha parênteses espaço abre parênteses tabela linha com n linha com 2 fim da tabela fecha parênteses espaço abre parênteses tabela linha com n linha com 3 fim da tabela fecha parênteses espaço abre parênteses tabela linha com n linha com 4 fim da tabela fecha parênteses... abre parênteses tabela linha com n linha com n fim da tabela fecha parênteses espaço$

Ao calcular os valores dos coeficientes, encontramos a seguinte representação do triângulo de Pascal:

Propriedades

1.ª) Todas as linhas têm o número 1 como seu primeiro e último elemento.

De fato, o primeiro elemento de todas as linhas é calculado por:

$abre parênteses tabela linha com n linha com 0 fim da tabela fecha parênteses igual a numerador n fatorial sobre denominador 0 fatorial parêntese esquerdo n menos 0 parêntese direito fatorial fim da fração igual a numerador n fatorial sobre denominador 0 fatorial n fatorial fim da fração igual a 1 espaço espaço espaço espaço espaço espaço espaço parêntese esquerdo c o n s i d e r a n d o espaço 0 fatorial igual a 1 parêntese direito$

e o último elemento de todas as linhas é calculado por:

$abre parênteses tabela linha com n linha com n fim da tabela fecha parênteses igual a numerador n fatorial sobre denominador n fatorial fim da fração igual a 1$

2.ª) O restante dos números de uma linha é formado pela adição dos dois números mais próximos da linha acima.

Essa propriedade é chamada de Relação de Stifel e é expressa por:

$abre parênteses tabela linha com célula com n menos 1 fim da célula linha com célula com p menos 1 fim da célula fim da tabela fecha parênteses mais abre parênteses tabela linha com célula com n menos 1 fim da célula linha com p fim da tabela fecha parênteses igual a abre parênteses tabela linha com n linha com p fim da tabela fecha parênteses$

É possível verificar a relação de Stifel diretamente no triângulo de Pascal, porque a partir da segunda linha, cada elemento é igual à soma do elemento acima com o seu anterior.

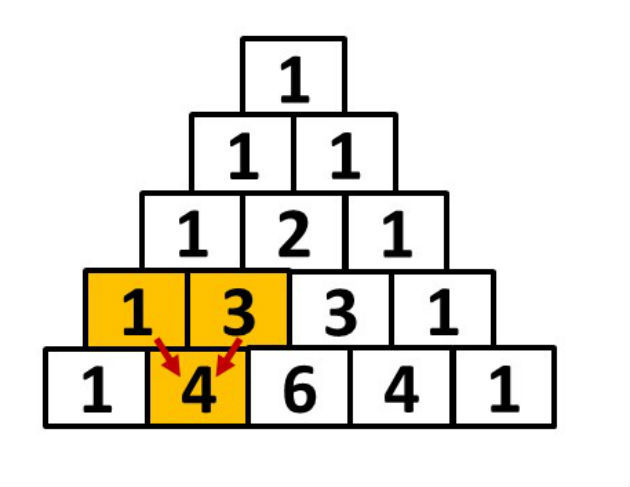
3.ª) Os elementos de uma mesma linha equidistantes dos extremos têm valores iguais.

$abre parênteses tabela linha com n linha com p fim da tabela fecha parênteses igual a abre parênteses tabela linha com n linha com célula com n menos p fim da célula fim da tabela fecha parênteses seta para a direita p mais parêntese esquerdo n menos p parêntese direito igual a n espaço espaço espaço parêntese esquerdo n ú m e r o s espaço b i n o m i a i s espaço c o m p l e m e n t a r e s parêntese direito$

Exemplos

a) $abre parênteses tabela linha com 4 linha com 1 fim da tabela fecha parênteses igual a abre parênteses tabela linha com 4 linha com 3 fim da tabela fecha parênteses seta para a direita 1 mais 3 igual a 4$

b) $abre parênteses tabela linha com 6 linha com 2 fim da tabela fecha parênteses igual a abre parênteses tabela linha com 6 linha com 4 fim da tabela fecha parênteses seta para a direita 2 mais 4 igual a 6$

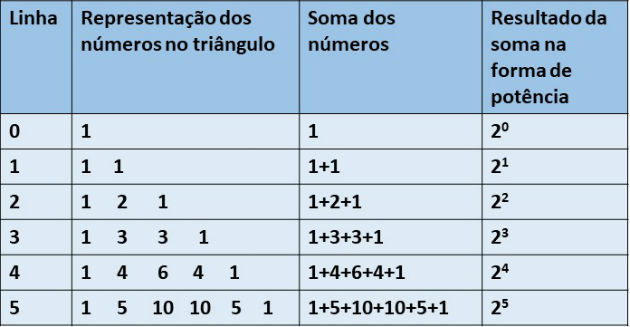
4.ª) A soma dos elementos de uma linha de numerador (n) será igual a 2ⁿ.

Observe a tabela abaixo:

Binômio de Newton

O Binômio de Newton é a potência da forma (x+y)ⁿ, sendo x e y números reais e n um número natural. Para valores pequenos de n a expansão do binômio pode ser feita multiplicando seus fatores.

Contudo, para expoentes maiores esse método pode se tornar muito trabalhoso. Assim, podemos recorrer ao triângulo de Pascal para determinar dos coeficientes binomiais dessa expansão.

Podemos representar a expansão do binômio (x+y)ⁿ, como:

$parêntese esquerdo x mais y parêntese direito à potência de n igual a abre parênteses tabela linha com n linha com 0 fim da tabela fecha parênteses x à potência de n mais abre parênteses tabela linha com n linha com 1 fim da tabela fecha parênteses x à potência de n menos 1 fim do exponencial y mais abre parênteses tabela linha com n linha com 2 fim da tabela fecha parênteses x à potência de n menos 2 fim do exponencial y ao quadrado mais... mais abre parênteses tabela linha com n linha com k fim da tabela fecha parênteses x à potência de n menos k fim do exponencial y à potência de k mais... mais abre parênteses tabela linha com n linha com n fim da tabela fecha parênteses y à potência de n$

Note que os coeficientes da expansão correspondem aos números binomiais, e esses números são os que formam o triângulo de Pascal.

Assim, para determinar os coeficientes da expansão (x+y)ⁿ , devemos considerar a linha n correspondente do triângulo de Pascal.

Exemplo

Desenvolva o binômio (x + 3)⁶:

Solução:

Como o expoente do binômio é igual a 6, iremos utilizar os números relativos a 6.ª linha do triângulo de Pascal para os coeficientes dessa expansão. Assim, temos:

6ª linha do triângulo de Pascal: 1 6 15 20 15 6 1

Esses números serão os coeficientes do desenvolvimento do binômio.

(x + 3)⁶ = 1 . x⁶. 3⁰+ 6 . x⁵. 3¹+15 . x⁴. 3²+ 20 . x³. 3³+ 15 . x². 3⁴+ 6 . x¹. 3⁵+1. x⁰. 3⁶

Resolvendo as operações encontramos a expansão do binômio:

(x + 3)⁶ = x⁶ +18 . x⁵ +135 x⁴ + 540 x³ + 1215 x² + 1458 x + 729

Para saber mais, leia também:

Exercícios Resolvidos

1) Determine o 7º termo do desenvolvimento de (x+1)⁹.

Ver Resposta

84x³

2) Calcule o valor das expressões abaixo, usando as propriedades do triângulo de Pascal.

$a parêntese direito espaço abre parênteses tabela linha com 4 linha com 0 fim da tabela fecha parênteses mais abre parênteses tabela linha com 4 linha com 1 fim da tabela fecha parênteses mais abre parênteses tabela linha com 4 linha com 2 fim da tabela fecha parênteses mais abre parênteses tabela linha com 4 linha com 3 fim da tabela fecha parênteses mais abre parênteses tabela linha com 4 linha com 4 fim da tabela fecha parênteses$

$b parêntese direito espaço abre parênteses tabela linha com 6 linha com 4 fim da tabela fecha parênteses mais abre parênteses tabela linha com 6 linha com 2 fim da tabela fecha parênteses$

$c parêntese direito espaço abre parênteses tabela linha com 7 linha com 3 fim da tabela fecha parênteses mais abre parênteses tabela linha com 7 linha com 4 fim da tabela fecha parênteses$

Ver Resposta

a) 2⁴ = 16
b) 30
c) 70

Pratique mais com:

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.