Triângulo Retângulo

Rafael C. Asth

Professor de Matemática e Física

O triângulo retângulo é uma figura geométrica formada por três lados. Ele possui um ângulo reto, cuja medida é de 90º, e dois ângulos agudos, menores que 90º.

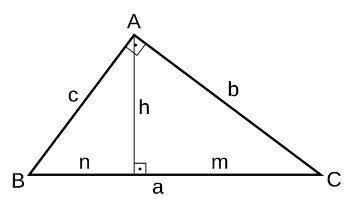
Triângulo Retângulo

Representação de um triângulo retângulo

Principais Características

Lados do Triângulo Retângulo

O lado oposto ao ângulo de 90º é chamado hipotenusa. Esse é o maior dos três lados da figura.

Os demais lados são denominados de cateto adjacente e cateto oposto.

Note que a hipotenusa no triângulo ABC acima, é representada como a (lado BC) e os catetos como b (lado AC) e c (lado AB).

Em relação aos lados dos triângulos, temos a classificação:

Triângulo Equilátero: possui os três lados iguais.
Triângulo Isósceles: possui dois lados iguais, e um diferente.
Triângulo Escaleno: possui os três lados diferentes.

Ângulos do Triângulo Retângulo

Como ocorre em todos os triângulos, a soma dos ângulos internos do triângulo retângulo é de 180º.

Os vértices dos ângulos são representados por (A), (B) e (C). Já o "h" é a altura relativa à hipotenusa.

Portanto, conforme a figura acima temos:

A é um ângulo reto: 90º
B e C são ângulos agudos, ou seja, são menores que 90º

Feita essa observação, o triângulo retângulo possui dois ângulos complementares, donde a soma dos dois ângulos medem 90º.

A + B = 90°.

Em relação aos ângulos internos dos triângulos, temos a classificação:

Triângulo Retângulo: possui um ângulo interno reto (90º).
Triângulo Acutângulo: todos os ângulos internos são agudos, ou seja, as medidas dos ângulos são menores que 90º.
Triângulo Obtusângulo: Um ângulo interno é obtuso, ou seja, possui um ângulo com medida maior do que 90º.

Área do Triângulo Retângulo

Para calcular a área de um triângulo retângulo, utiliza-se a seguinte expressão:

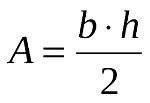
Onde,

A: área
b: base
h: altura

Perímetro do Triângulo Retângulo

O perímetro de uma figura geométrica, corresponde a soma de todos os lados. Ela é calculada pela seguinte fórmula:

P = L+L+L
ou
P = 3L

Onde,

P: perímetro
L: lados

Trigonometria no Triângulo Retângulo

A trigonometria é a área que estuda as relações existentes nos triângulos que possuem um ângulo reto (90º). As relações trigonométricas num triângulo retângulo são:

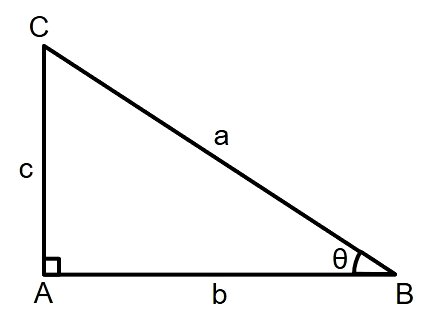
Seno

$sen espaço reto teta igual a numerador cateto espaço oposto sobre denominador hipotenusa fim da fração igual a reto c sobre reto a$

Cosseno

$cos espaço reto teta espaço igual a numerador cateto espaço adjacente sobre denominador hipotenusa fim da fração igual a reto b sobre reto a$ cateto adjacente/hipotenusa

Tangente

$tan espaço reto teta igual a numerador cateto espaço oposto sobre denominador cateto espaço adjacente fim da fração igual a reto c sobre reto b$

Teorema de Pitágoras

O Teorema de Pitágoras é, talvez, o mais importante da matemática. Esse teorema afirma que para qualquer triângulo retângulo, o quadrado da hipotenusa equivale à soma dos quadrados dos catetos. É representado da seguinte forma:

$começar estilo tamanho matemático 18px reto a ao quadrado espaço igual a espaço reto b ao quadrado espaço mais espaço reto c ao quadrado fim do estilo$

Exercícios de triângulo retângulo com gabarito

Exercício 1

(Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:

a) 6√3 m.
b) 12 m.
c) 13,6 m.
d) 9√3 m.
e) 18 m.

Ver Resposta

Alternativa e: 18 m.

$s e n espaço 30 º igual a numerador c a t e t o espaço o p o s t o sobre denominador h i p o t e n u s a fim da fração$

De uma tabela trigonométrica temos que sen 30º é igual a 0,5. O cateto oposto ao ângulo de 30º é a altura do triângulo e o comprimento é a hipotenusa.

$sen espaço 30 º igual a reto h sobre 36 reto h igual a sen espaço 30 º espaço. espaço 36 reto h igual a 0 vírgula 5 espaço. espaço 36 reto h igual a 18 espaço reto m$

Exercício 2

(Enem-2013) As torres Puerta de Europa são duas torres inclinadas uma contra a outra, construídas numa avenida de Madri, na Espanha.

A inclinação das torres é de 15° com a vertical e elas têm, cada uma, uma altura de 114 m (a altura é indicada na figura como o segmento AB).

Estas torres são um bom exemplo de um prisma oblíquo de base quadrada e uma delas pode ser observada na imagem.

Utilizando 0,26 como valor aproximado para a tangente de 15° e duas casas decimais nas operações, descobre-se que a área da base desse prédio ocupa na avenida um espaço

a) menor que 100 m².
b) entre 100 m² e 300 m².
c) entre 300 m² e 500 m².
d) entre 500 m² e 700 m².
e) maior que 700 m².

Ver Resposta

Alternativa e: maior que 700 m².

Como a base é um quadrado, precisamos determinar o lado para determinar a área.

A torre faz um ângulo de 15º com a vertical e utilizando a altura AB de 114 m, é possível determinar a base L

$tan espaço 15 º igual a L sobre 114 L igual a 114 espaço. espaço tan espaço 15 º L igual a 114 espaço. espaço 0 vírgula 26 L igual a 29 vírgula 64$

A área do quadrado é determinada por L . L = L²

$A igual a espaço L ao quadrado A igual a 29 vírgula 64 espaço. espaço 29 vírgula 64 A aproximadamente igual espaço 878 vírgula 53 espaço m ao quadrado$

A resposta é então a alternativa e, sendo a área maior que 700 m².

Exercício 3

(UFAM) Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente, então a tangente do ângulo oposto ao menor lado é:

a) 2√3
b) √3/3
c) √3/6
d) √20/20
e) 3√3

Ver Resposta

Alternativa b: √3/3.

Para determinar o terceiro lado utilizamos o teorema de Pitágoras.

$abre parênteses 4 a fecha parênteses ao quadrado igual a abre parênteses 2 a fecha parênteses ao quadrado mais L ao quadrado 16 a ao quadrado igual a 4 a ao quadrado mais L ao quadrado 16 a ao quadrado menos 4 a ao quadrado igual a L ao quadrado 12 a ao quadrado igual a L ao quadrado raiz quadrada de 12. a ao quadrado fim da raiz igual a L raiz quadrada de 12. raiz quadrada de a ao quadrado fim da raiz igual a L a raiz quadrada de 12 igual a L$

Fatorando o 12, temos

$L igual a 2 raiz quadrada de 3 a$

Como $2 raiz quadrada de 3 a maior que 2 a$ o menor lado é o de medida 2a.

A partir do ângulo oposto ao lado 2a, a tangente será:

$tan espaço igual a espaço numerador 2 a sobre denominador 2 raiz quadrada de 3 a fim da fração tan igual a numerador 1 sobre denominador raiz quadrada de 3 fim da fração$

Racionalizando para tirar o raiz do denominador:

$numerador 1 sobre denominador raiz quadrada de 3 fim da fração. numerador raiz quadrada de 3 sobre denominador raiz quadrada de 3 fim da fração igual a numerador raiz quadrada de 3 sobre denominador raiz quadrada de 9 fim da fração igual a numerador raiz quadrada de 3 sobre denominador 3 fim da fração$

Desta forma, a resposta é a opção b.

Aprenda mais com:

Triângulo: tudo sobre este polígono

Rafael C. Asth

Professor de Matemática, licenciado e pós-graduado em ensino da Matemática e da Física. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.