Ângulos Notáveis

Rafael C. Asth

Professor de Matemática e Física

Os ângulos de 30°, 45º e 60º são chamados de notáveis, por serem os que com mais frequência calculamos.

Sendo assim, é importante conhecer os valores do seno, cosseno e tangente desses ângulos.

Tabela dos ângulos notáveis

A tabela abaixo é muito útil e pode ser facilmente construída, seguindo os passos indicados.

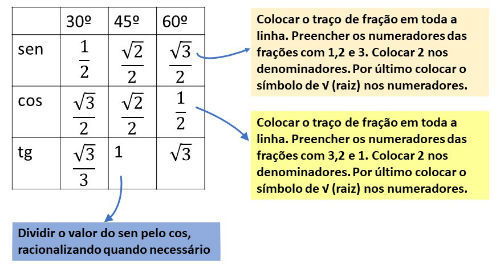
Caso queira aprender mais sobre ângulos.

Valor do seno e do cosseno de 30º e 60º

Os ângulos de 30º e 60º são complementares, ou seja, somam 90º.

Encontramos o valor do seno de 30º calculando a razão entre o cateto oposto e a hipotenusa. Já o valor do cosseno de 60º é a razão entre o cateto adjacente e a hipotenusa.

Desta forma, o seno de 30º e o cosseno de 60º do triângulo representado abaixo, será dado por:

Assim, identificamos que o valor do seno de 30º é igual ao valor do cosseno de 60º. O mesmo acontece com o seno de 60º e o cosseno de 30º, pois:

Portanto, quando dois ângulos são complementares, o valor do seno de um é igual ao valor do cosseno do outro.

Para encontrar o valor do seno de 30º (cosseno de 60º) e o cosseno de 30º (seno de 60º), consideremos um triângulo equilátero ABC de lados iguais a L, representado abaixo:

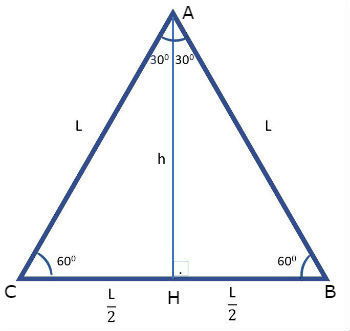
A altura (h) do triângulo equilátero coincide com a mediana, assim, a altura divide o lado relativo ao meio ().

Além disso, a altura coincide com a bissetriz. Desta forma, o ângulo também fica dividido ao meio, conforme mostrado na figura.

Vamos ainda considerar que o valor da altura é dado por:

.

Para calcular o seno e o cosseno de 30º, consideraremos o triângulo retângulo AHB, que foi obtido a partir do triângulo ABC.

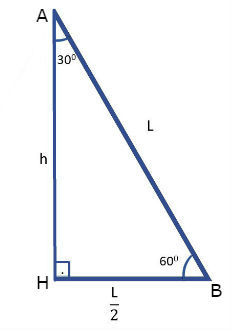
Assim, temos:

e

Aprenda mais sobre o triângulo retângulo.

Valor do seno e do cosseno de 45º

Calcularemos o valor do seno e do cosseno do ângulo de 45º, a partir de um quadrado de lado L representado abaixo:

A diagonal do quadrado é a bissetriz do ângulo, ou seja, a diagonal divide o ângulo ao meio (45º). Além disso, a diagonal d mede .

Para encontrar o valor do seno e do cosseno de 45º consideramos o triângulo retângulo ABC indicado na figura:

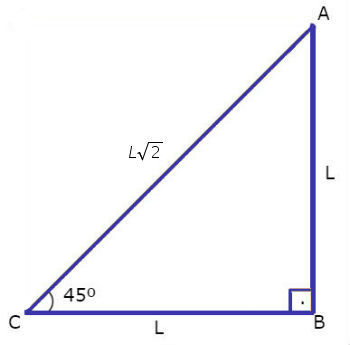
Então:

e

Valor da tangente de 30º, 45º e 60º

Para calcular a tangente dos ângulos notáveis usaremos a razão trigonométrica:

Assim:

Exercícios ângulos notáveis

Exercício 1

Um nadador atravessa um rio, seguindo um ângulo de 30° com uma das margens. Sabendo que a largura do rio mede 40 m, determine a distância percorrida pelo nadador para atravessar o rio.

Exercício 2

(Enem - 2010) Um balão atmosférico, lançado em Bauru (343 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo
previsto de medição.

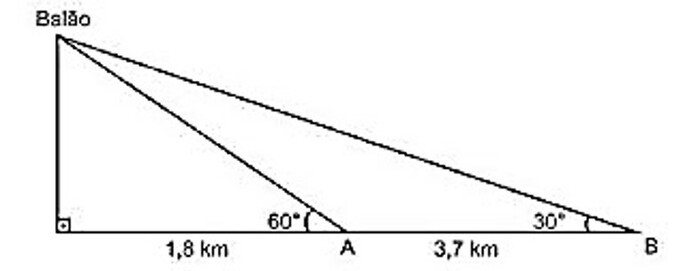
Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60º; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30º.

Qual a altura aproximada em que se encontrava o balão?

a) 1,8km
b) 1,9km
c) 3,1km
d) 3,7km
e) 5,5km

Para saber mais, leia também:

• Tabela Trigonométrica
• Seno, cosseno e tangente
• Trigonometria no Triângulo Retângulo

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.