Razões Trigonométricas
As razões (ou relações) trigonométricas estão relacionadas com os ângulos de um triângulo retângulo. As principais são: o seno, o cosseno e a tangente.
As relações trigonométricas são resultado da divisão entre as medidas de dois lados de um triângulo retângulo, e por isso são chamadas de razões.
Razões Trigonométricas no Triângulo Retângulo
O triângulo retângulo recebe esse nome pois apresenta um ângulo chamado de reto, que possui o valor de 90°.
Os outros ângulos do triângulo retângulo são menores que 90°, chamados de ângulos agudos. A soma dos ângulos internos é de 180°.
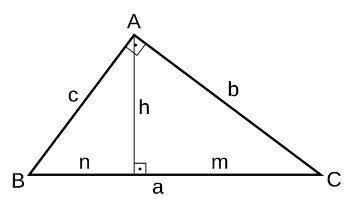
Observe que os ângulos agudos de um triângulo retângulo são chamados de complementares. Ou seja, se um deles tem medida x, o outro terá a medida (90°- x).
Lados do Triângulo Retângulo: Hipotenusa e Catetos
Antes de mais nada, temos que saber que no triângulo retângulo, a hipotenusa é o lado oposto ao ângulo reto e o maior lado do triângulo. Já os catetos são os lados adjacentes e que formam o ângulo de 90°.
Note que dependendo dos lados de referência ao ângulo, temos o cateto oposto e o cateto adjacente.
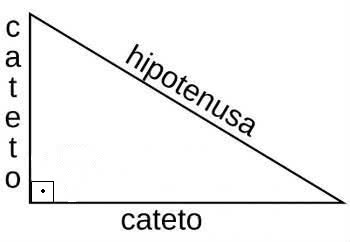
Feita essa observação, as razões trigonométricas no triângulo retângulo são:
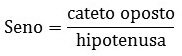
Lê-se cateto oposto sobre a hipotenusa.
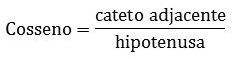
Lê-se cateto adjacente sobre a hipotenusa.
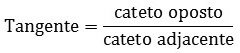
Lê-se cateto oposto sobre o cateto adjacente.
Vale lembrar que pelo conhecimento de um ângulo agudo e a medida de um dos lados de um triângulo retângulo, podemos descobrir o valor dos outros dois lados.
Saiba mais:
- Lei dos Senos
- Lei dos Cossenos
- Seno, Cosseno e Tangente
- Relações Trigonométricas
- Identidades trigonométricas
- Trigonometria no Triângulo Retângulo
- Exercícios sobre razões trigonométricas
Ângulos Notáveis
Os chamados ângulos notáveis são os que surgem com maior frequência nos estudos de razões trigonométricas.
Veja a tabela abaixo com o valor dos ângulos de 30°; 45° e 60°:
| Relações Trigonométricas | 30° | 45° | 60° |
|---|---|---|---|
| Seno | 1/2 | √2/2 | √3/2 |
| Cosseno | √3/2 | √2/2 | 1/2 |
| Tangente | √3/3 | 1 | √3 |
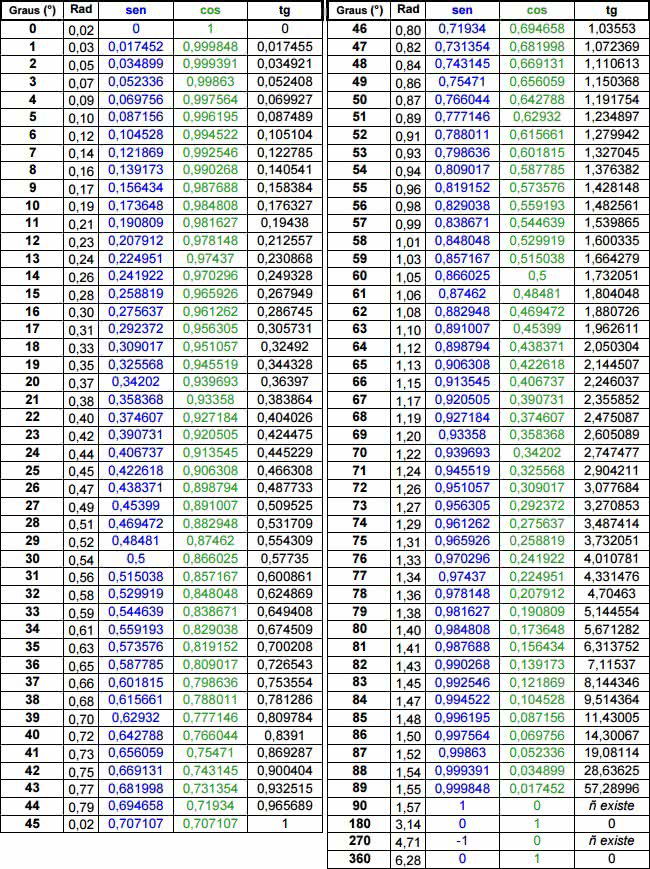
Tabela Trigonométrica
A tabela trigonométrica apresenta os ângulos em graus e os valores decimais do seno, cosseno e tangente. Confira abaixo a tabela completa:
Saiba mais sobre o tema:
- Relações Métricas no Triângulo Retângulo
- Círculo Trigonométrico
- Funções Trigonométricas
- Fórmulas de Matemática
- Exercícios de Trigonometria no triângulo retângulo
- Exercícios de seno, cosseno e tangente
Aplicações
As razões trigonométricas possuem muitas aplicações. Assim, conhecendo os valores do seno, cosseno e tangente de um ângulo agudo, podemos fazer diversos cálculos geométricos.
Um exemplo notório, é o cálculo realizado para descobrir o comprimento de uma sombra ou de um prédio.
Exemplo
Qual o comprimento da sombra de uma árvore de 5m de altura quando o sol está a 30° acima do horizonte?
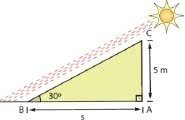
Tg B = AC / AB = 5/s
Uma vez que B = 30° temos que a:
Tg B = 30° = √3/3 = 0,577
Logo,
0,577 = 5/s
s = 5/0,577
s = 8,67
Portanto, o tamanho da sombra é de 8,67 metros.
Exercícios de Vestibular com Gabarito
1. (UFAM) Se um cateto e a hipotenusa de um triângulo retângulo medem 2a e 4a, respectivamente, então a tangente do ângulo oposto ao menor lado é:
a) 2√3
b) √3/3
c) √3/6
d) √20/20
e) 3√3
2. (Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:
a) 6√3 m.
b) 12 m.
c) 13,6 m.
d) 9√3 m.
e) 18 m.
3. (UEPB) Duas ferrovias se cruzam segundo um ângulo de 30°. Em km, a distância entre um terminal de cargas que se encontra numa das ferrovias, a 4 km do cruzamento, e a outra ferrovia, é igual a:
a) 2√3
b) 2
c) 8
d) 4√3
e) √3
Leia também: Exercícios de trigonometria
GOUVEIA, Rosimar. Razões Trigonométricas. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/razoes-trigonometricas/. Acesso em:


