Círculo Trigonométrico

O Círculo Trigonométrico, também chamado de Ciclo ou Circunferência Trigonométrica, é uma representação gráfica que auxilia no cálculo das razões trigonométricas.

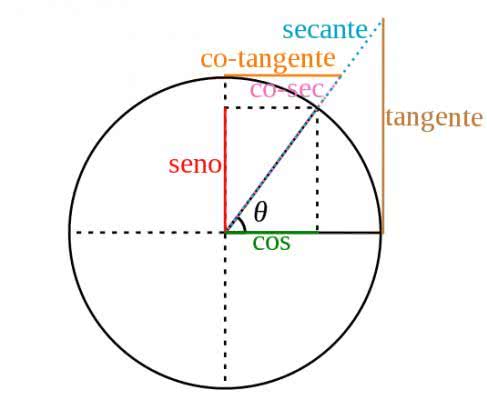
Círculo trigonométrico e as razões trigonométricas

De acordo com a simetria do círculo trigonométrico temos que o eixo vertical corresponde ao seno e o eixo horizontal ao cosseno. Cada ponto dele está associado aos valores dos ângulos.Radianos do Círculo Trigonométrico

A medida de um arco no círculo trigonométrico pode ser dada em grau (°) ou radiano (rad).

• 1° corresponde a 1/360 da circunferência. A circunferência é dividida em 360 partes iguais ligadas ao centro, sendo que cada uma delas apresenta um ângulo que corresponde a 1°.
• 1 radiano corresponde à medida de um arco da circunferência, cujo comprimento é igual ao raio da circunferência do arco que será medido.

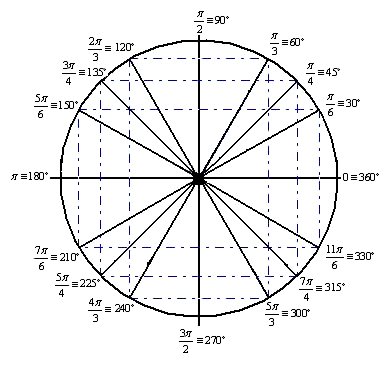Figura do Círculo Trigonométrico dos ângulos expressos em graus e radianos

Para auxiliar nas medidas, confira abaixo algumas relações entre graus e radianos:

• π rad = 180°
• 2π rad = 360°
• π/2 rad = 90°
• π/3 rad = 60°
• π/4 rad = 45°

Obs: Se quiser converter essas unidades de medidas (grau e radiano) utiliza-se a regra de três.

Exemplo: Qual a medida de um ângulo de 30° em radianos?

π rad -180°
x – 30°
x = 30° . π rad/180°
x = π/6 rad

Quadrantes do Círculo Trigonométrico

Quando dividimos o círculo trigonométrico em quatro partes iguais, temos os quatro quadrantes que o constituem. Para compreender melhor, observe a figura abaixo:

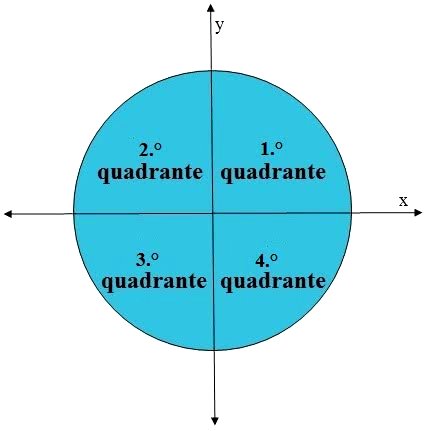
• 1.° Quadrante: 0º
• 2.° Quadrante: 90º
• 3.° Quadrante: 180º
• 4.° Quadrante: 270º

Círculo Trigonométrico e seus Sinais

De acordo com o quadrante em que está inserido, os valores do seno, cosseno e tangente variam.

Ou seja, os ângulos podem apresentar um valor positivo ou negativo.

Para compreender melhor, veja a figura abaixo:

Como Fazer o Círculo Trigonométrico?

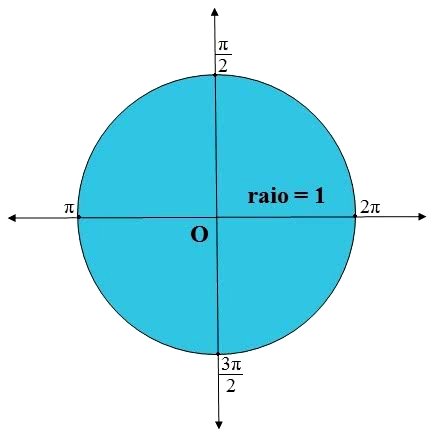
Para fazer um círculo trigonométrico, devemos construí-lo sobre o eixo de coordenadas cartesianas com centro em O. Ele apresenta um raio unitário e os quatro quadrantes.

Razões Trigonométricas

As razões trigonométricas estão associadas às medidas dos ângulos de um triângulo retângulo.

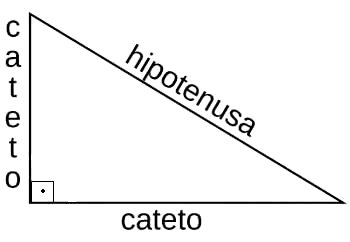
Representação do triângulo retângulo com seus catetos e a hipotenusa

Elas são definidas pelas razões de dois lados de um triângulo retângulo e do ângulo que forma, sendo classificadas em seis maneiras:

Seno (sen)

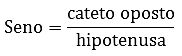
Lê-se cateto oposto sobre a hipotenusa.

Cosseno (cos)

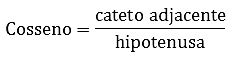
Lê-se cateto adjacente sobre a hipotenusa.

Tangente (tan)

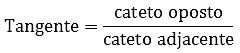
Lê-se cateto oposto sobre cateto adjacente.

Cotangente (cot)

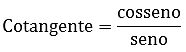
Lê-se cosseno sobre seno.

Cossecante (csc)

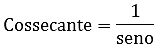
Lê-se um sobre seno.

Secante (sec)

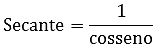
Lê-se um sobre cosseno

Ângulos Notáveis

No círculo trigonométrico podemos representar as razões trigonométricas de um ângulo qualquer da circunferência.

Chamamos de ângulos notáveis aqueles mais conhecidos (30°, 45° e 60°). As razões trigonométricas mais importantes são seno, cosseno e tangente:

Relações Trigonométricas	30°	45°	60°
Seno	1/2	√2/2	√3/2
Cosseno	√3/2	√2/2	1/2
Tangente	√3/3	1	√3

Saiba tudo sobre Trigonometria:

• Trigonometria
• Identidades trigonométricas
• Trigonometria no Triângulo Retângulo
• Relações Trigonométricas
• Funções Trigonométricas
• Triângulo Retângulo
• Seno, Cosseno e Tangente
• Lei dos Senos
• Radiano: o que é e como e medir

Exercícios de círculo trigonométrico com Gabarito

Exercício 1

(Vunesp-SP) Em um jogo eletrônico o “monstro” tem a forma de um setor circular de raio 1 cm, como mostra a figura.

A parte que falta no círculo é a boca do “monstro”, e o ângulo de abertura mede 1 radiano. O perímetro “do monstro”, em cm, é:

a) π – 1
b) π + 1
c) 2 π – 1
d) 2 π
e) 2 π + 1

Exercício 2

(PUC-MG) Os moradores de certa cidade costumam fazer caminhada em torno de duas de suas praças. A pista que contorna uma dessas praças é um quadrado de lado L e tem 640 m de extensão; a pista que contorna a outra praça é um círculo de raio R e tem 628 m de extensão. Nessas condições, o valor da razão R/L é aproximadamente igual a:

Use π = 3,14.

a) 1/2
b) 5/8
c) 5/4
d) 3/2

Exercício 3

(U.F.Pelotas-RS) Nossa época, marcada pela luz elétrica, por estabelecimentos comerciais abertos 24 horas e prazos apertados de trabalho, que muitas vezes exigem o sacrifício dos períodos de sono, pode muito bem ser considerada a era do bocejo. Estamos dormindo menos. A ciência mostra que isso contribui para a ocorrência de males como diabetes, depressão e obesidade. Por exemplo, quem não segue a recomendação de dormir no mínimo de 8 horas por noite, tem 73% mais risco de se tornar obeso. (Revista Saúde, n.º 274, junho de 2006 - adaptado)

Uma pessoa que durma à zero hora e siga a recomendação do texto apresentado, quanto ao número mínimo de horas diárias de sono, acordará às 8 horas da manhã. O ponteiro das horas, que mede 6 cm de comprimento, do despertador dessa pessoa, terá descrito, durante seu período de sono, um arco de circunferência com comprimento igual a:

Use π = 3,14.

a) 6π cm
b) 32π cm
c) 36π cm
d) 8π cm
e) 18π cm

Exercício 4

(UFRS) Os ponteiros de um relógio marcam duas horas e vinte minutos. O menor ângulos entre os ponteiros é:

a) 45°
b) 50°
c) 55°
d) 60°
e) 65°

Pratique mais exercícios sobre círculo trigonométrico com resposta.