Relações Trigonométricas

Rosimar Gouveia

Professora de Matemática e Física

As relações trigonométricas são relações entre valores das funções trigonométricas de um mesmo arco. Essas relações também são chamadas de identidades trigonométricas.

Inicialmente a trigonometria tinha como objetivo o cálculo das medidas dos lados e ângulos dos triângulos.

Nesse contexto, as razões trigonométricas sen θ , cos θ e tg θ são definidas como relações entre os lados de um triângulo retângulo.

Dado um triângulo retângulo ABC com um ângulo agudo θ, conforme figura abaixo:

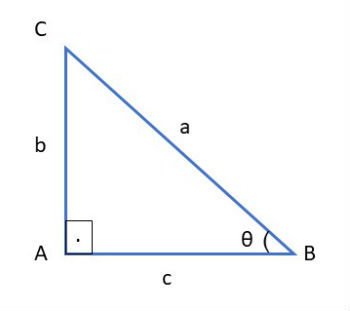
triângulo retângulo

Definimos as razões trigonométricas seno, cosseno e tangente em relação ao ângulo θ, como:

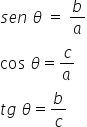
Sendo,

a: hipotenusa, ou seja, lado oposto ao ângulo de 90º
b: cateto oposto ao ângulo θ
c: cateto adjacente ao ângulo θ

Para saber mais, leia também Lei dos Cossenos e Lei dos Senos

Relações fundamentais

A trigonometria ao longo dos anos foi se tornando mais abrangente, não se restringindo apenas aos estudos dos triângulos.

Dentro deste novo contexto, define-se o círculo unitário, também chamado de circunferência trigonométrica. Ele é utilizado para estudar as funções trigonométricas.

Circunferência trigonométrica

A circunferência trigonométrica é uma circunferência orientada de raio igual a 1 unidade de comprimento. Associamos a ela um sistema de coordenadas cartesianas.

Os eixos cartesianos dividem a circunferência em 4 partes, chamadas de quadrantes. O sentido positivo é anti-horário, conforme figura abaixo:

Usando a circunferência trigonométrica, as razões que a princípio foram definidas para ângulos agudos (menores que 90º), passam a ser definidas para arcos maiores de 90º.

Para isso, associamos um ponto P, cuja abscissa é o cosseno de θ e cuja ordenada é o seno de θ.

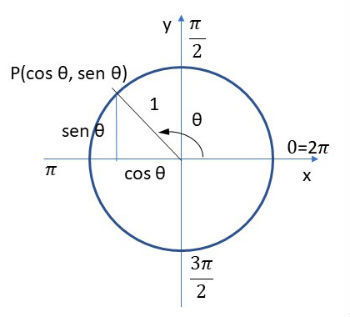
Como todos os pontos da circunferência trigonométrica estão a uma distância de 1 unidade da origem, podemos usar o teorema de Pitágoras. O que resulta na seguinte relação trigonométrica fundamental:

Podemos definir ainda a tg x, de um arco de medida x, no círculo trigonométrico como sendo:

Outras relações fundamentais:

Cotangente do arco de medida x

Secante do arco de medida x.

Cossecante do arco de medida x.

Relações trigonométricas derivadas

Partido das relações apresentadas, podemos encontrar outras relações. Abaixo, mostramos duas importantes relações decorrentes das relações fundamentais.

Aprenda mais sobre identidades trigonométricas.

Para saber mais, leia também:

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações