ASSINAR TODA MATÉRIA+

Exercícios sobre razões trigonométricas

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física

As razões trigonométricas: seno, cosseno e tangente, são relações entre os lados de um triângulo retângulo. Com o uso destas razões é possível determinar valores desconhecidos de ângulos e medidas de lados.

Pratique seu conhecimento com as questões resolvidas.

Questões sobre seno

Questão 1

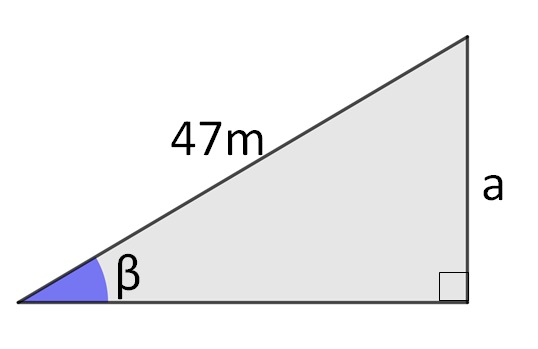
Sendo o ângulo beta igual a 30° e a hipotenusa 47 m, calcule a medida da altura a do triângulo.

A razão trigonométrica seno é o quociente entre as medidas do cateto oposto ao ângulo, e a hipotenusa.

s e n espaço beta espaço igual a espaço numerador c a t e t o espaço o p o s t o sobre denominador h i p o t e n u s a fim da fração s e n espaço beta espaço igual a espaço a sobre 47

Isolando a de um lado da igualdade, temos:

a espaço igual a espaço 47. espaço s e n espaço beta
A partir de uma tabela trigonométrica, temos que seno de 30° é igual a 1 meio, substituindo na equação:

a espaço igual a espaço 47.1 meio igual a 23 vírgula 5

Portanto, a altura do triângulo é de 23,50 m.

Questão 2

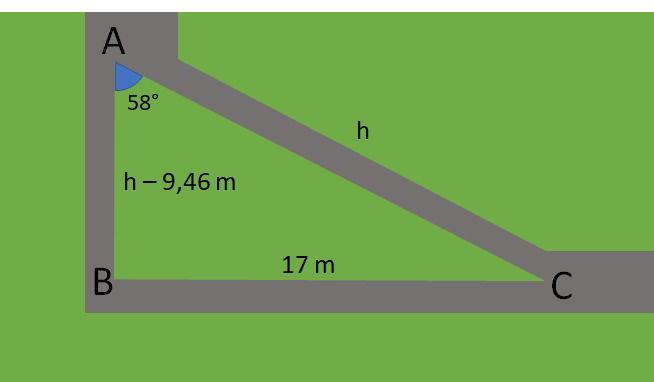
A vista superior de um parque mostra dois caminhos para se chegar ao ponto C, a partir do ponto A. Uma das opções é ir para B, onde há bebedouros e lugares de descanso e, depois ir para C. Caso um visitante do parque queira ir direto para C, quantos metros ele terá caminhado a menos do que a primeira opção?

Considerar as aproximações:
sen 58° = 0,85
cos 58° = 0,53
tan 58° = 1,60

Resposta: saindo de A e indo direto para C, a caminhada é 7,54 m mais curta.

Passo 1: calcular h

s e n espaço 58 sinal de grau igual a 17 sobre h h igual a numerador 17 sobre denominador s e n espaço 58 sinal de grau fim da fração h igual a numerador 17 sobre denominador 0 vírgula 85 fim da fração igual a 20 espaço m

Passo 2: determinar a distância AB com barra sobrescrito.

h espaço menos espaço 9 vírgula 46 20 espaço menos espaço 9 vírgula 46 espaço igual a espaço 10 vírgula 54 espaço m

Passo 3: determinar a distância AB com barra sobrescrito espaço mais espaço BC com barra sobrescrito.

AB com barra sobrescrito mais BC com barra sobrescrito igual a 10 vírgula 54 espaço mais espaço 17 igual a espaço 27 vírgula 54 espaço m

Passo 4: determinar a diferença entre os dois caminhos.

parêntese esquerdo pilha A B com barra acima mais pilha B C com barra acima parêntese direito menos AC com barra sobrescrito igual a 27 vírgula 54 menos 20 igual a 7 vírgula 54 espaço m

Questão 3

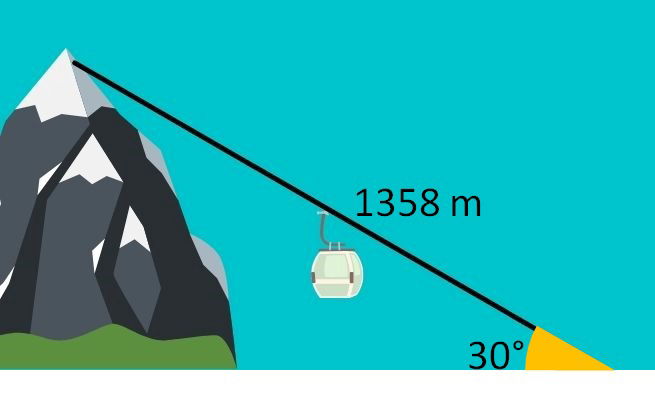
Um teleférico foi instalado ligando uma base ao cume de uma montanha. Para a instalação, foram utilizados 1358 m de cabos, dispostos a uma angulação de 30° em relação ao solo. Qual a altura da montanha?

Resposta correta: a altura da montanha é de 679 m.

Podemos usar a razão trigonométrica seno para determinar a altura da montanha.

De uma tabela trigonométrica, temos que sen 30° = 0,5. Como o seno é a razão entre o cateto oposto e a hipotenusa, determinamos a altura.

s e n 30 sinal de grau igual a numerador c a t e t o espaço o p o s t o sobre denominador h i p o t e n u s a fim da fração s e n 30 sinal de grau igual a numerador a l t u r a espaço d a espaço m o n tan h a sobre denominador c o m p r i m e n t o espaço d o s espaço c a b o s fim da fração 0 vírgula 5 igual a numerador a l t u r a espaço d a espaço m o n tan h a sobre denominador 1358 fim da fração 0 vírgula 5 espaço. espaço 1358 espaço igual a espaço a l t u r a espaço d a espaço m o n tan h a 679 espaço m espaço igual a espaço espaço a l t u r a espaço d a espaço m o n tan h a

Questão 4

(CBM-SC, soldado-2010) Para socorrer uma pessoa num apartamento durante um incêndio, os bombeiros utilizarão uma escada de 30m, que será colocada conforme a figura a seguir formando com o solo um ângulo de 60º. Qual a distância do apartamento ao chão? (Utilize sen60º=0,87; cos60º=0,5 e tg60º= 1,73)

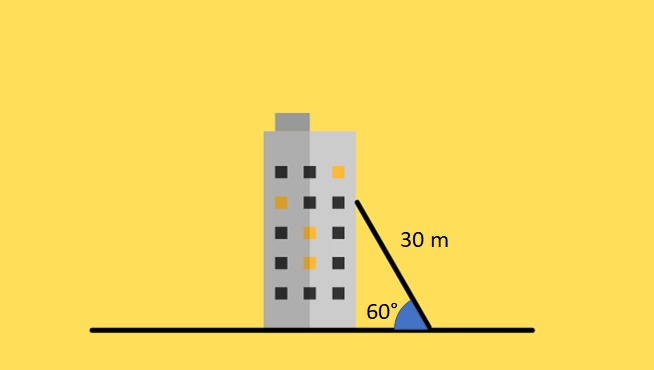
a) 15 m.
b) 26,1 m.
c) 34,48 m.
d) 51,9 m.

Resposta correta: b) 26,1 m.

Para determinar a altura, utilizaremos o seno de 60°. Chamando a altura de h e utilizando seno de 60° igual a 0,87.

s e n espaço 60 sinal de grau igual a h sobre 30 h igual a 30 espaço. espaço s e n espaço 60 sinal de grau h igual a 30 espaço. espaço 0 vírgula 87 h igual a 26 vírgula 1 espaço m.

Questões sobre cosseno

Questão 5

Cosseno é a razão entre o cateto adjacente a um ângulo e a medida da hipotenusa. Sendo alfa igual a 45°, calcule a medida do cateto adjacente ao ângulo alpha, no triângulo da figura.

Considere cos espaço 45 sinal de grau igual a numerador raiz quadrada de 2 sobre denominador 2 fim da fração

cos espaço 45 sinal de grau igual a c sobre 28 28 espaço. espaço cos espaço 45 sinal de grau igual a c 28 espaço. espaço numerador raiz quadrada de 2 sobre denominador 2 fim da fração igual a c 14 raiz quadrada de 2 igual a c

Aproximando o valor da raiz quadra de 2:

14.1 vírgula 41 aproximadamente igual c 19 vírgula 74 espaço aproximadamente igual c

A medida do cateto adjacente é de, aproximadamente, 19,74 m.

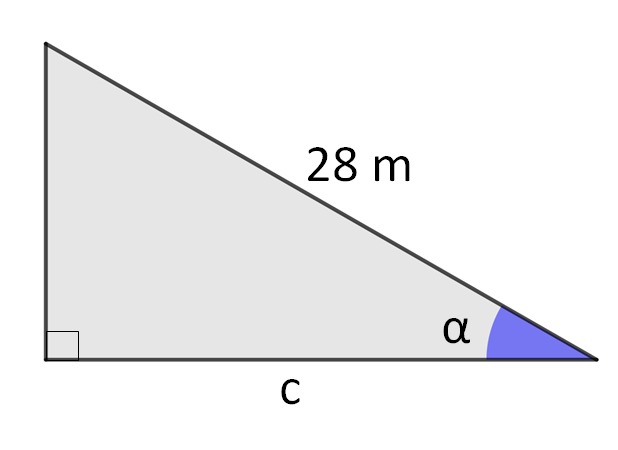
Questão 6

Durante uma partida de futebol, o jogador 1 faz um lançamento para o jogador 2 com um ângulo de 48°. Qual a distância que a bola deverá percorrer até chegar ao jogador 2?

Considere:
sen 48° = 0,74
cos 48° = 0,66
tan 48° = 1,11

Resposta correta: A bola deverá percorrer uma distância de 54,54 m.

A medida entre o jogador 1 e o jogador 2 é a hipotenusa do triângulo retângulo.

O cosseno do ângulo de 48° é a razão entre seu cateto adjacente e a hipotenusa, onde, o cateto adjacente é a distância entre o meio de campo e a grande área.

52,5 - 16,5 = 36 m

Fazendo o cálculo do cosseno, sendo h a hipotenusa.

cos espaço 48 sinal de grau igual a 36 sobre h h igual a numerador 36 sobre denominador cos espaço 48 sinal de grau fim da fração h igual a numerador 36 sobre denominador 0 vírgula 66 fim da fração h aproximadamente igual 54 vírgula 54 espaço m

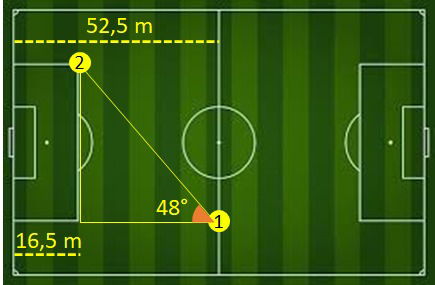
Questão 7

Um telhado é tido como de duas águas quando há dois caimentos. Em uma obra está sendo construído um telhado onde, o encontro de suas duas águas esteja exatamente no meio da lage. O ângulo de inclinação de cada água em relação a lage é de 30°. A lage possui 24 m de comprimento. Para encomendar as telhas antes mesmo da estrutura que irá sustentar o telhado estar concluída, é preciso conhecer o comprimento de cada água, que será de:

Como a lage possui 24 m de comprimento, cada lado terá 12 m.
Chamando o comprimento de cada água do telhado de L, temos:

cos espaço 30 sinal de grau igual a 12 sobre L L igual a numerador 12 sobre denominador cos espaço 30 sinal de grau fim da fração L igual a numerador 12 sobre denominador começar estilo mostrar numerador raiz quadrada de 3 sobre denominador 2 fim da fração fim do estilo fim da fração igual a numerador 2.12 sobre denominador raiz quadrada de 3 fim da fração igual a numerador 24 sobre denominador raiz quadrada de 3 fim da fração

Racionalizando a fração para tirar o número irracional raiz quadrada de 3 do denominador.

numerador 24 sobre denominador raiz quadrada de 3 fim da fração. numerador raiz quadrada de 3 sobre denominador raiz quadrada de 3 fim da fração igual a numerador 24 raiz quadrada de 3 sobre denominador raiz quadrada de 9 fim da fração igual a numerador 24 raiz quadrada de 3 sobre denominador 3 fim da fração igual a 8 raiz quadrada de 3

Fazendo, raiz quadrada de 3 aproximadamente igual 1 vírgula 7

L igual a 8 raiz quadrada de 3 igual a 8.1 vírgula 7 igual a 13 vírgula 6 espaço m

Portanto, o comprimento de cada água do telhado será de, aproximadamente, 13,6 m.

Questões sobre tangente

Questão 8

Tangente é a razão entre o cateto oposto a um ângulo, e seu cateto adjacente. Sendo o ângulo alfa igual a 60°, calcule a altura do triângulo.

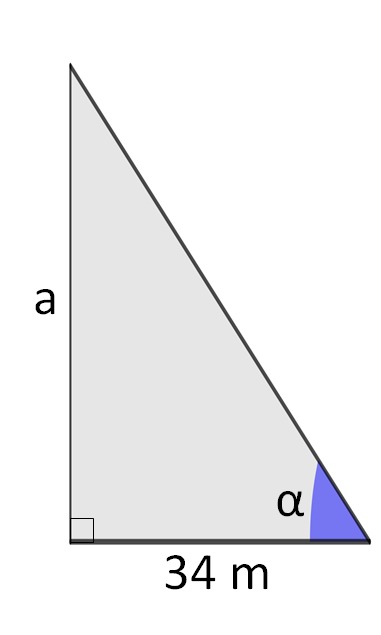
tan espaço alfa igual a a sobre 34 a espaço igual a espaço 34 espaço. espaço tan espaço alfa a igual a 34 espaço. espaço tan espaço 60 a igual a 34. raiz quadrada de 3 espaço m

Questão 9

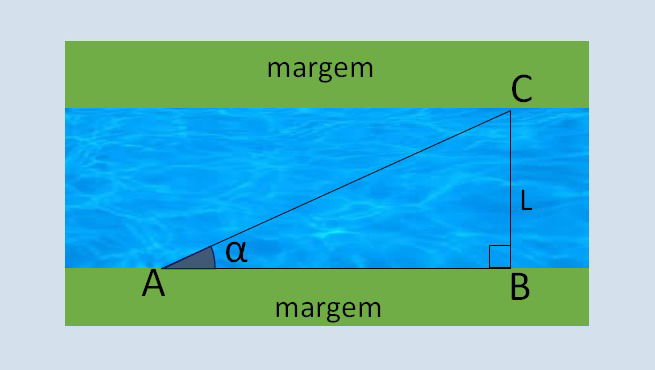
Uma pessoa quer conhecer a largura de um rio antes de atravessá-lo. Para isso, ela fixa um ponto de referência na outra margem, como uma árvore, por exemplo (ponto C). Na posição em que se encontra (ponto B), caminha 10 metros para a esquerda, até se forme um ângulo de 30° entre o ponto A e o ponto C. Calcule a largura do rio.

Considere raiz quadrada de 3 igual a 1 vírgula 73.

Para calcular a largura do rio que chamaremos de L, utilizaremos a tangente do ângulo alfa.

tan espaço alfa espaço igual a espaço L sobre 10 L igual a espaço 10 espaço. espaço tan espaço alfa L igual a espaço 10 espaço. espaço numerador raiz quadrada de 3 sobre denominador 3 fim da fração L igual a 10 espaço. espaço numerador 1 vírgula 73 sobre denominador 3 fim da fração L igual a numerador 17 vírgula 3 sobre denominador 3 fim da fração L aproximadamente igual 5 vírgula 76 espaço m

Questão 10

(Enem 2020) Pergolado é o nome que se dá a um tipo de cobertura projetada por arquitetos, comumente em praças e jardins, para criar um ambiente para pessoas ou plantas, no qual há uma quebra da quantidade de luz,
dependendo da posição do sol. É feito como um estrado de vigas iguais, postas paralelas e perfeitamente
em fila, como ilustra a figura.

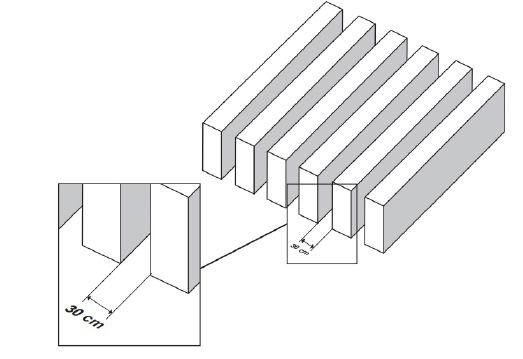
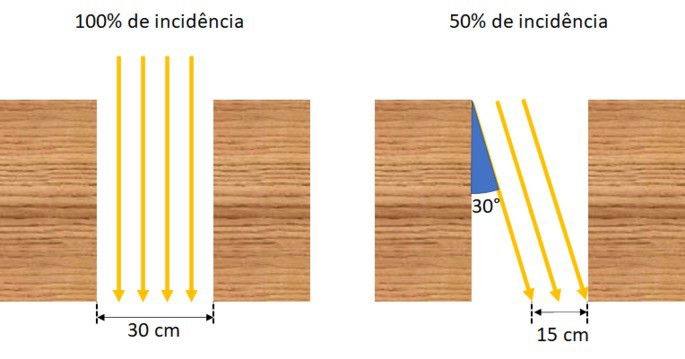
Um arquiteto projeta um pergolado com vãos de 30 cm de distância entre suas vigas, de modo que, no
solstício de verão, a trajetória do sol durante o dia seja realizada num plano perpendicular à direção das
vigas, e que o sol da tarde, no momento em que seus raios fizerem 30° com a posição a pino, gere a metade
da luz que passa no pergolado ao meio-dia.
Para atender à proposta do projeto elaborado pelo arquiteto, as vigas do pergolado devem ser
construídas de maneira que a altura, em centímetro, seja a mais próxima possível de

a) 9.
b) 15.
c) 26.
d) 52.
e) 60.

Resposta correta: c) 26.

Para compreender a situação, faremos um esboço.

A imagem da esquerda mostra a incidência de luz solar ao meio de dia, com 100%. A imagem da direita é que nos interessa. Ela permite que apenas 50% dos raios solares passem pelo pergolado, com a inclinação de 30%.

Utilizamos a razão trigonométrica tangente. A tangente de um ângulo é a razão entre o cateto oposto e o cateto adjacente.

Chamando a altura da peça do pergolado de h, temos:

tan espaço 30 sinal de grau igual a 15 sobre h h igual a numerador espaço 15 sobre denominador tan espaço 30 sinal de grau fim da fração

Fazendo tangente de 30° = numerador raiz quadrada de 3 sobre denominador 3 fim da fração

h igual a numerador 15 sobre denominador começar estilo mostrar numerador raiz quadrada de 3 sobre denominador 3 fim da fração fim do estilo fim da fração igual a numerador 3.15 sobre denominador raiz quadrada de 3 fim da fração igual a numerador 45 sobre denominador raiz quadrada de 3 fim da fração

Vamos racionalizar a última fração para não deixar a raiz de três, um número irracional, no denominador.

numerador 45 sobre denominador raiz quadrada de 3 fim da fração. numerador raiz quadrada de 3 sobre denominador raiz quadrada de 3 fim da fração igual a numerador 45 raiz quadrada de 3 sobre denominador raiz quadrada de 9 fim da fração igual a numerador 45 raiz quadrada de 3 sobre denominador 3 fim da fração igual a 15 raiz quadrada de 3

Fazendo, raiz quadrada de 3 aproximadamente igual 1 vírgula 7

15.1 vírgula 7 igual a 25 vírgula 5

Das opções disponíveis pela questão, a que mais se aproxima é a letra c, a altura das vigas devem possuir, aproximadamente, 26cm.

Questão 11

(Enem 2010) Um balão atmosférico, lançado em Bauru (343 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando
agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França,
Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu
após o cumprimento do tempo previsto de medição.

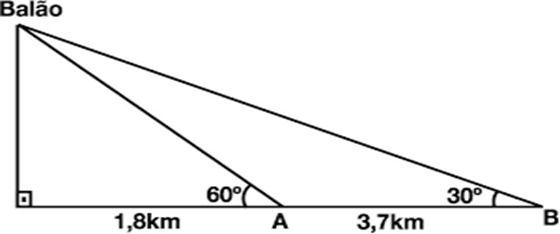
Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão
e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a
primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°.
Qual a altura aproximada em que se encontrava o balão?

a) 1,8 km
b) 1,9 km
c) 3,1 km
d) 3,7 km
e) 5,5 km

Resposta correta: c) 3,1 km

Utilizamos a tangente de 60° que é igual raiz quadrada de 3. A tangente é a razão trigonométrica entre o cateto oposto ao ângulo e seu adjacente.

tan espaço 60 sinal de grau igual a numerador h sobre denominador 1 vírgula 8 fim da fração h igual a 1 vírgula 8 espaço. espaço tan espaço 60 sinal de grau h igual a 1 vírgula 8 espaço. espaço raiz quadrada de 3 h aproximadamente igual 3 vírgula 11 espaço k m

Portanto, a altura do balão era de, aproximadamente, 3,1 km.

Pratique mais com:

Aprenda mais:

Rafael C. Asth
Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também
Leitura Recomendada
Tópicos Relacionados
Exercícios Exercícios de Matemática
Que tal um up?
Toda Matéria+
Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo
Exercícios exclusivos Acesso a centenas de questões com gabaritos
Estude sem publicidade Navegação limpa e focada para evitar distrações
Assinar Toda Matéria+
Toda Matéria no YouTube
Thumbnail Toda Matéria no Youtube
Toda Matéria Inscreva-se