Comprimento da Circunferência: como calcular, fórmula e exemplos

Rafael C. Asth

Professor de Matemática e Física

O comprimento de uma circunferência é a medida da união de todos os pontos que a formam, sendo expressa em alguma unidade de comprimento como: metro, centímetro ou milímetros, por exemplo.

A circunferência também é a borda do círculo, por isso, e calculamos a medida de seu comprimento da mesma forma.

Um modo prático para obter este comprimento é utilizar uma fita métrica flexível ou, desfazendo a circunferência, a esticando em linha reta para, assim, medir.

Como nem sempre é possível desfazer a circunferência ou utilizar uma fita métrica, obtemos esta medida por um cálculo, utilizando a medida do raio.

Comprimento da circunferência

Para calcular o comprimento de uma circunferência multiplicamos três valores: o número 2, o número $reto pi$ (pi) e a medida do raio da circunferência.

Fórmula do comprimento da circunferência

$começar estilo tamanho matemático 18px reto C igual a 2. reto pi. reto r fim do estilo$

Onde:

C é a medida do comprimento;
$reto pi$ (pi) é um número irracional, aproximadamente 3,14;
r é a medida do raio, segmento que liga o centro a um ponto qualquer na circunferência.

A unidade de medida é a mesma utilizada na medição do raio.

Outra forma de escrever esta fórmula é substituir o 2 e o r por d, onde d é o diâmetro da circunferência.
Como o diâmetro é igual a duas vezes o raio, d = 2.r, a fórmula também pode ser escrita da seguinte forma:

$começar estilo tamanho matemático 18px reto C igual a reto d. reto pi fim do estilo$

Exemplo 1
Determine o comprimento de uma circunferência que possui diâmetro de 1,70 m. Considere $reto pi espaço igual a 3 vírgula 14 espaço$ .

Substituindo na fórmula com o diâmetro, temos:

$reto C espaço igual a espaço reto d espaço. espaço reto pi reto C espaço igual a espaço 1 vírgula 70 espaço. espaço 3 vírgula 14 reto C espaço igual a espaço 5 vírgula 338 espaço$

Portanto, o comprimento da circunferência é de 5,338 m.

Exemplo 2
Uma circunferência de raio igual a 1,5 cm, possui quantos centímetros de comprimento?

Utilizando a fórmula do comprimento da circunferência em função do raio, temos:

$começar estilo tamanho matemático 14px reto C espaço igual a espaço 2 espaço. espaço reto pi espaço. espaço reto r reto C espaço igual a espaço 2 espaço. espaço 3 vírgula 14 espaço. espaço 1 vírgula 5 reto C espaço igual a espaço 9 vírgula 42 fim do estilo$

Portanto, o comprimento desta circunferência é de 9,42 cm.

Dedução da fórmula do comprimento da circunferência

A fórmula para o cálculo do comprimento da circunferência vem de um fato curioso: ao dividir o comprimento de qualquer circunferência pela medida de seu diâmetro, sempre se obtêm o número $pi$ (pi), não importa seu tamanho.

$numerador comprimento espaço da espaço circunferência espaço sobre denominador diâmetro espaço da espaço circunferência espaço fim da fração espaço igual a espaço reto pi$

Chamando o comprimento da circunferência de C e seu diâmetro de d, temos:

$reto C sobre reto d igual a reto pi$

Isolando o comprimento da circunferência, obtemos:

$reto C espaço igual a espaço reto d espaço. espaço reto pi$

Ou, como o diâmetro é igual a duas vezes a medida do raio, podemos substituir d por 2r, e obter a fórmula:

$reto C espaço igual a espaço 2 espaço. espaço reto pi espaço. espaço reto r espaço$

Exercícios sobre circunferência resolvidos

Exercício 1

(Enem 2015) A figura é uma representação simplificada do carrossel de um parque de diversões, visto de cima. Nessa representação, os cavalos estão identificados pelos pontos escuros, e ocupam circunferências de raios 3 m e 4 m, respectivamente, ambas centradas no ponto O.

Em cada sessão de funcionamento, o carrossel efetua 10 voltas.

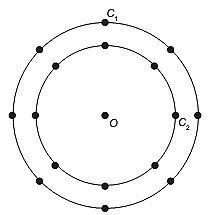
Quantos metros uma criança sentada no cavalo C1 percorrerá a mais do que uma criança no cavalo C2, em uma sessão? Use 3,0 como aproximação para π.

a) 55,5
b) 60,0
c) 175,5
d) 235,5
e) 240,0

Ver Resposta

Resposta correta: b) 60,0.

Resolução

Dados:
Raios de 3 e 4 metros para C2 e C1, respectivamente.
$pi espaço$ = 3
Sessão de 10 voltas.

Objetivo: determinar quanto C1 percorre a mais que C2 em dez voltas.

Diferença = C1 - C2

Passo 1: determinar o comprimento de cada circunferência.

Aplicando os dados na fórmula do comprimento da circunferência temos:

$C 2 espaço igual a espaço 2 espaço. espaço pi espaço. espaço r C 2 espaço igual a espaço 2 espaço. espaço 3 espaço. espaço 3 espaço igual a espaço 18 m e C 1 espaço igual a espaço 2 espaço. espaço 3 espaço. espaço 4 espaço igual a espaço 24 m$

Passo 2: comprimento total percorrido em 10 voltas.

C2 = 18 . 10 = 180m

C1 = 24 . 10 = 240m

Conclusão
Fazendo a diferença entre entre C1 e C2,

C1 - C2 = 240 - 180 = 60m

Portanto, a criança no cavalo 1, percorrerá 60m a mais que a criança no cavalo 2.

Exercício 2

(Marinha 2016) Na figura abaixo, o triângulo ABC está inscrito na circunferência de centro O. Sabendo que AB= 4 cm e AC= 2√5 cm, determine a medida do comprimento da circunferência.

Use $pi espaço igual a espaço 3 vírgula 14$

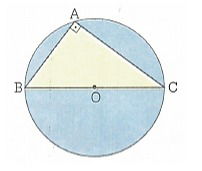
a) 18,84 cm
b) 12,05 cm
c) 10,16 cm
d) 9 cm
e) 3 cm

Ver Resposta

Resposta correta: a) 18,84 cm

Resolução

Objetivo: determinar o comprimento da circunferência.

Estratégia: determinar a medida do diâmetro BC e usa-la para determinar o comprimento da circunferência.

Para o cálculo do comprimento da circunferência, precisamos determinar o diâmetro ou raio. Na figura, o segmento BC é o diâmetro da circunferência e, ao mesmo tempo, a hipotenusa de do triângulo retângulo ABC.

Cálculo de BC
Usando o Teorema de Pitágoras temos,

$B C ao quadrado igual a B A ao quadrado espaço mais espaço A C ao quadrado$

Substituindo os valores fornecidos no enunciado,

$B C ao quadrado igual a 4 ao quadrado espaço mais espaço parêntese esquerdo 2 raiz quadrada de 5 parêntese direito ao quadrado B C à potência de 2 fim do exponencial igual a 16 espaço mais espaço 4 espaço. espaço 5 B C ao quadrado igual a 16 espaço mais espaço 20 B C ao quadrado igual a 36 B C espaço igual a raiz quadrada de 36 B C espaço igual a espaço 6$

Desta forma, o diâmetro BC é igual a 6 cm.

Cálculo do comprimento da circunferência

Utilizando a fórmula do comprimento da circunferência temos,

$C espaço igual a d espaço. espaço pi$

Onde d é o diâmetro BC. Substituindo os valores:

$C espaço igual a espaço 6 espaço. espaço 3 vírgula 14 C espaço igual a espaço 18 vírgula 84$

Conclusão
Desta forma, o comprimento da circunferência é de 18,84 cm.

Veja também:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações