Estudo dos Gases

Rosimar Gouveia

Professora de Matemática e Física

O estudo dos gases compreende a análise da matéria quando se apresenta no estado gasoso, sendo este o seu estado termodinâmico mais simples.

Um gás é composto por átomos e moléculas e nesse estado físico, um sistema apresenta pouca interação entre suas partículas.

Devemos notar que um gás é diferente do vapor. Normalmente consideramos um gás quando a substância encontra-se no estado gasoso em temperatura e pressão ambiente.

Já as substâncias que se apresentam no estado sólido ou líquido em condições ambientes, quando estão no estado gasoso são chamadas de vapor.

Variáveis de estado

Podemos caracterizar um estado de equilíbrio termodinâmico de um gás através das variáveis de estado: pressão, volume e temperatura.

Quando conhecemos o valor de duas das variáveis de estado podemos encontrar o valor da terceira, pois elas estão inter-relacionadas.

Volume

Como existe uma grande distância entre os átomos e moléculas que compõem um gás, a força de interação entre suas partículas é muito fraca.

Por isso, os gases não possuem forma definida e ocupam todo o espaço onde estão contidos. Além disso, podem ser comprimidos.

Pressão

As partículas que compõem um gás exercem força sobre as paredes de um recipiente. A medida dessa força por unidade de área representa a pressão do gás.

A pressão de um gás está relacionada com o valor médio da velocidade das moléculas que o compõem. Desta forma, temos uma ligação entre uma grandeza macroscópica (pressão) com uma microscópica (velocidade das partículas).

Temperatura

A temperatura de um gás representa a medida do grau de agitação das moléculas. Desta forma, a energia cinética média de translação das moléculas de um gás é calculada através da medida da sua temperatura.

Utilizamos a escala absoluta para indicar o valor da temperatura de um gás, ou seja, a temperatura é expressa na escala Kelvin.

Veja também: Transformações Gasosas

Gás Ideal

Sob determinadas condições, a equação de estado de um gás pode ser bastante simples. Um gás que apresenta essas condições é chamado de gás ideal ou gás perfeito.

As condições necessárias para que um gás seja considerado perfeito são:

• Ser constituído por um número muito grande de partículas em movimento desordenado;
• O volume de cada molécula ser desprezível em relação ao volume do recipiente;
• As colisões são elásticas de curtíssima duração;
• As forças entre as moléculas são desprezíveis, exceto durante as colisões.

Na verdade, o gás perfeito é uma idealização do gás real, entretanto, na prática podemos muitas vezes utilizar essa aproximação.

Quanto mais a temperatura de um gás se distanciar do seu ponto de liquefação e a sua pressão for reduzida, mais próximo estará de um gás ideal.

Equação geral dos gases ideais

A lei dos gases ideais ou equação de Clapeyron descreve o comportamento de um gás perfeito em termos de parâmetros físicos e nos permite avaliar o estado macroscópio do gás. Ela é expressa como:

P.V = n.R.T

Sendo,

P: pressão do gás (N/m²)
V: volume (m³)
n: número de moles (mol)
R: constante universal dos gases (J/K.mol)
T: temperatura (K)

Constante universal dos gases

Se considerarmos 1 mol de um determinado gás, a constante R pode ser encontrada pelo produto da pressão com o volume dividido pela temperatura absoluta.

De acordo com a Lei de Avogadro, em condições normais de temperatura e pressão (temperatura é igual a 273,15 K e pressão de 1 atm) 1 mol de um gás ocupa um volume igual a 22,415 litros. Assim, temos:

Fazendo as devidas transformações, podemos ainda expressar a constante dos gases como sendo igual a:

R = 8,314 J/K.mol ou 1,986 cal/k.mol

Exercícios Resolvidos

1) UERJ - 2016

Para descrever o comportamento dos gases ideais em função do volume V, da pressão P e da temperatura T, podem ser utilizadas as seguintes equações:

De acordo com essas equações, a razão é aproximadamente igual a:

2) UFPR - 2014

A equação geral dos gases ideais é uma equação de estado que correlaciona pressão, temperatura, volume e quantidade de matéria, sendo uma boa aproximação ao comportamento da maioria dos gases.

Os exemplos descritos a seguir correspondem às observações realizadas para uma quantidade fixa de matéria de gás e variação de dois parâmetros. Numere as representações gráficas relacionando-as com as seguintes descrições.

1. Ao encher um balão com gás hélio ou oxigênio, o balão apresentará a mesma dimensão.
2. Ao encher um pneu de bicicleta, é necessária uma pressão maior que a utilizada em pneu de carro.
3. O cozimento de alimentos é mais rápido em maiores pressões.
4. Uma bola de basquete cheia no verão provavelmente terá aparência de mais vazia no inverno, mesmo que não tenha vazado ar.

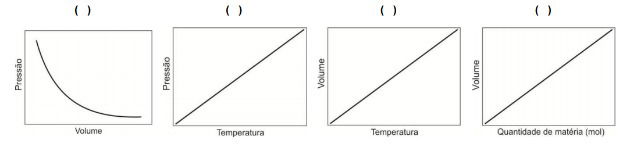
Assinale a alternativa que apresenta a sequência correta na numeração das representações gráficas.

a) 1 – 3 – 4 – 2.
b) 2 – 3 – 4 – 1.
c) 4 – 2 – 1 – 3.
d) 4 – 3 – 1 – 2.
e) 2 – 4 – 3 – 1.

Conheça também a Transformação Isobárica e a Transformação Adiabática.

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.