Exercícios sobre a força elástica (com gabarito explicado)
A força elástica está presente em diversos objetos do nosso dia a dia — de molas e elásticos a instrumentos de medição e sistemas de amortecimento. Dominar esse conceito é essencial para compreender como esses materiais respondem a deformações e como a Lei de Hooke descreve esse comportamento.
Para ajudar você a revisar o tema de forma prática, preparamos uma série de exercícios sobre força elástica, todos com gabarito explicado passo a passo para reforçar o entendimento e evitar os erros mais comuns.
Questão 1
Em uma aula de treinamento funcional, um estudante utiliza um equipamento conhecido como extensor elástico para fortalecer a musculatura dos ombros.
O fabricante do equipamento informa no manual que o elástico se comporta como uma mola ideal e possui uma constante elástica k igual a 400 N/m.
Quando o equipamento está em repouso (sem ser esticado), o elástico possui um comprimento total de 50 cm.
Durante o exercício, o estudante segura as extremidades e estica o elástico até que ele atinja um comprimento total de 90 cm.
Desprezando a massa do elástico e eventuais perdas de energia, qual é a intensidade da força elástica que o equipamento exerce sobre as mãos do estudante nesse momento de extensão máxima?
a) 160 N
b) 200 N
c) 360 N
d) 1.600 N
Resposta correta: alternativa a) 160 N
Para resolver essa questão, precisamos aplicar a Lei de Hooke, cuja fórmula é:
Fel = k . x
Onde:
- Fel é a força elástica em Newtons, N
- k é a constante elástica da mola em N/m
- x é a deformação da mola ou o quanto ela esticou ou comprimiu, em metros.
Vamos primeiro determinar a deformação (x) do elástico.
O erro mais comum é usar o comprimento total final ou o inicial na fórmula. A Lei de Hooke usa a deformação (x), que é a diferença entre o comprimento final e o comprimento inicial (quando o elástico está em repouso). O enunciado trouxe:
Comprimento inicial Lel = 50 cm
Comprimento final L = 90 cm
Então:
x = L − L0
x = 90 cm − 50 cm = 40 cm = 0,4 m
Vamos agora calcular a força elástica usando a Lei de Hooke. Substituímos os valores na fórmula, temos:
F0= 400 . 0,4 = 160 N
Questão 2
Maria trabalha em uma empresa de brinquedos e está testando o sistema de amortecimento de um novo modelo de carrinho de controle remoto.
O sistema é composto por duas molas idênticas que funcionam de forma independente, cada uma com constante elástica de 250 N/m.
Durante um teste de impacto, Maria observa que:
- A primeira mola comprimiu 8 cm
- A segunda mola comprimiu 4 cm
Considerando que as molas se comportam de acordo com a Lei de Hooke, qual é a força elástica total que o sistema de amortecimento está exercendo sobre o carrinho nesse instante?
a) 10 N
b) 15 N
c) 20 N
d) 30 N
Resposta correta: alternativa d) 30 N.
Vamos primeiro organizar os dados do problema:
- Constante elástica de cada mola: k = 250 N/m
- Deformação da mola 1: x1 = 8 cm = 0,08 m
- Deformação da mola 2: x2 = 4 cm = 0,04 m
Vamos calcular a força elástica na primeira mola, aplicando a Lei de Hooke:
F1 = k .x2
F1 = 250 . 0,08 =20 N
Vamos agora calcular a força elástica na segunda mola, aplicando também a Lei de Hooke:
F1= k . x1
F2 = 250 . 0,04 = 10 N
Vamos então calcular a força total do sistema. Como as molas atuam de forma independente e na mesma direção (ambas empurrando o carrinho), a força total é igual à soma das forças individuais, ou:
F2= F2 + Ftotal
F1 = 20 + 10
F2= 30 N
Questão 3
Em uma feira de produtores locais, um agricultor utiliza uma balança analógica antiga, do tipo dinamômetro, para pesar suas mercadorias.
Essa balança funciona através da distensão de uma mola vertical localizada em seu interior.
Um cliente escolhe um saco de laranjas cuja massa total é de 3,0 kg.
Ao pendurar o saco de laranjas no gancho da balança e aguardar o sistema ficar em repouso, o agricultor nota que a mola sofreu uma deformação de 15 cm em relação ao seu comprimento original.
Considerando a aceleração da gravidade g = 10 m/s² e que a mola obedece à Lei de Hooke, qual é a constante elástica (k) da mola dessa balança?
a) 2 N/m
b) 20 N/m
c) 200 N/m
d) 250 N/m
Resposta correta: alternativa c) 200 N/m.
Para resolver esta questão devemos lembrar que, quando o saco de laranjas está parado em equilíbrio estático, a força total que atua sobre ele deve ser nula.
Assim, a força que a mola faz para segurá-lo (Força Elástica) deve ser igual ao peso do saco de laranjas.
Vamos primeiro calcular a Força Peso P do saco de laranja.
P = m . g
P = 3 kg . 10 m/s2 = 30 N
Assim, a força elástica que estica a mola é de 30 N.
Antes de usar a Lei de Hooke, vamos converter a deformação da mola para o Sistema Internacional, ou seja, metros:
x = 15 cm = 0,15 m
Podemos agora aplicar a Lei de Hooke:
Fel = k . x
30 N = k . 0,15 m
k = 30 N / 0,15 m
k = 200 N/m
Questão 4
Em um laboratório de controle de qualidade de uma fábrica de colchões, um técnico realiza testes em uma mola helicoidal para garantir que ela atende aos padrões de conforto.
O procedimento consiste em aplicar diferentes forças sobre a mola e medir a deformação resultante.
No primeiro teste, o técnico aplica uma força de 120 N e observa que a mola encolhe 4,0 cm.
Considerando que a mola se comporta como ideal obedecendo à Lei de Hooke dentro desse intervalo de testes, qual deve ser a intensidade da força aplicada para que essa mesma mola sofra uma deformação total de 10,0 cm?
a) 240 N
b) 300 N
c) 480 N
d) 1.200 N
Resposta correta: alternativa b) 300 N.
Essa questão pode ser resolvida de duas maneiras: usando a Lei de Hooke e encontrando o valor da constante elástica primeiro ou a proporcionalidade na Lei de Hooke, que é uma relação de primeira ordem entre a força e a deformação.
Vamos usar os dois métodos.
Método 1: Encontrando a Constante Elástica (k)
O primeiro teste nos permite determinar o valor de k ao substituir os valores dados na Lei de Hooke. Foram dados:
- F1 = 120 N
- x1 = 4,0 cm = 0,04 m
F1 = k . x1
120 = k . 0,04
k = 120 / 0,04 = 3000 N/m
Agora, tendo k e x1 , podemos calcular a força F1 para a nova deformação.
- x2 = 10,0 cm = 0,1 m
- k = 3000 N/m
F1= k . x1
F2 = 3000 . 0,1 = 300 N
Método 2: Por proporcionalidade
Como a Lei de Hooke (F2 = k . x) é uma função linear, a Força é diretamente proporcional à deformação.
Se a mola é a mesma, a constante k não muda, podemos dizer que:
F2 = k . x ⇒ k = F2 / x = constante
Então:
Questão 5
Durante uma aula prática de Física, um grupo de estudantes realizou um experimento para determinar a rigidez de uma mola helicoidal.
Eles aplicaram diferentes intensidades de força sobre a mola e mediram as respectivas deformações com uma régua, registrando os valores na tabela abaixo:
| Experimento | Força aplicada (N) | Deformação (cm) |
|---|---|---|
| 1 | 4,0 | 2,0 |
| 2 | 8,0 | 4,0 |
| 3 | 12,0 | 6,0 |
| 4 | 16,0 | 8,0 |
Observando a regularidade dos dados, os alunos confirmaram que a mola obedece à Lei de Hooke.
Com base na tabela apresentada, qual é o valor da constante elástica (k) dessa mola, expressa no Sistema Internacional em N/m?
a) 0,5 N/m
b) 2,0 N/m
c) 72 N/m
d) 200 N/m
Resposta correta: alternativa d) 200 N/m.
O primeiro passo é escolher um par de dados da tabela.
Como a mola obedece à Lei de Hooke e seu comportamento é linear, a razão entre a força e a deformação é constante.
Por isso você pode escolher qualquer linha da tabela.
Vamos usar, por exemplo, a linha 3 que possui:
- F3 = 12,0 N
- x3 = 6,0 cm = 0,06 m
Substituindo na Lei de Hooke, temos:
Fel = k . x
k = Fel / x
k = 12,0 / 0,06 = 200 N/m
Podemos verificar se a resposta está certa usando esse valor de K em qualquer outra linha da tabela. Vamos usar a linha 1 que possui, Fel = 4,0 N.
Nesse caso, temos:
Fel,1 = k . x1
4,0 = 200 . x1
x1 = 4,0 / 200 = 0,02 m = 2,0 cm
Chegamos ao valor da deformação da linha 1 da tabela, comprovando que o valor de k encontrado está correto.
Questão 6
Um engenheiro está projetando o sistema de suspensão de um carrinho de brinquedo.
Para escolher a mola ideal, ele submete uma mola de testes a diferentes forças e registra o quanto ela estica.
O comportamento dessa mola foi registrado no gráfico de força (F) em função da deformação (x) apresentado abaixo:
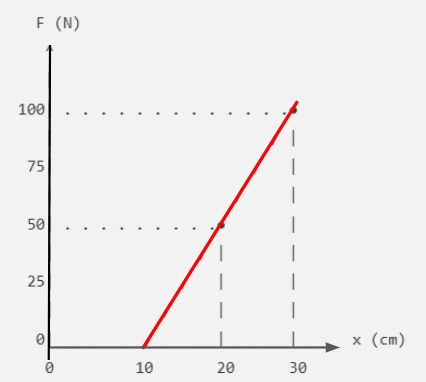
Analisando o gráfico, determine a constante elástica (k) dessa mola no Sistema Internacional de Unidades (N/m).
a) 250 N/m
b) 500 N/m
c) 1000 N/m
d) 1500 N/m
Resposta correta: alternativa b) 500 N/m
A primeira coisa que temos que fazer é interpretar o Gráfico.
Ele mostra uma reta partindo do ponto (10 cm, 0 N) ou x0 = 10 cm para F = 0N. Esse ponto indica o tamanho da mola quando ela está em repouso, ou seja, quando nenhuma força atura sobre ela.
Para calcular a constante k, precisamos escolher um ponto bem definido na reta. Podemos identificar dois pontos claros no gráfico:
- Ponto A: Força FA = 50 N com comprimento da mola xA = 20 cm.
- Ponto B: Força FB = 100 N com comprimento da mola xB = 30 cm.
Vamos escolher o Ponto B para o cálculo, mas o resultado seria o mesmo com o Ponto A, pois a Lei de Hooke é de primeira ordem.
Antes de substituir os valores do ponto B na Lei de Hooke, precisamos determinar a deformação da mola em metros. Lembre que a deformação da mola é dada por:
deformação = xA - xA = 30 cm - 10 cm = 20 cm = 0,2 m
Podemos agora usar a Lei de Hooke:
FB = k . xB
k = FB / xB
k = 100 N / 0,2 m = 500 N/m
Questão 7
Um grupo de estudantes do clube de robótica da escola está projetando um sistema de amortecimento para as "pernas" de um pequeno robô explorador.
Para escolher a mola ideal, eles realizaram um teste experimental em laboratório: suspenderam a mola verticalmente e foram adicionando diferentes pesos (forças) à sua extremidade, medindo o comprimento total da mola a cada adição.
Os dados coletados foram plotados no gráfico abaixo, que relaciona a Força Aplicada (F) com o Comprimento Total da mola (L):
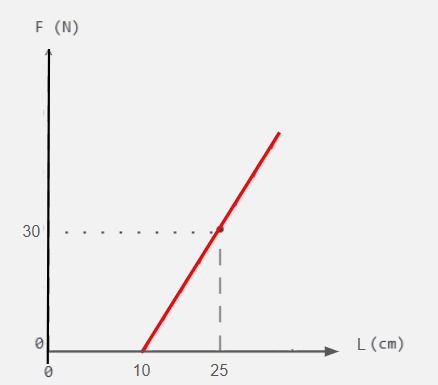
Com base no gráfico obtido pelos estudantes, determine, respectivamente: a constante elástica (k) dessa mola no Sistema Internacional de Unidades (N/m) e qual será o comprimento total da mola se for aplicada uma força de 50 N, assumindo que a mola não exceda seu limite elástico.
a) 120 N/m e 35 cm
b) 200 N/m e 25 cm
c) 200 N/m e 35 cm
d) 300 N/m e 30 cm
Resposta correta: alternativa c) 200 N/m e 35 cm.
A Lei de Hooke é dada pela fórmula:
Fel = k . x
Onde:
- F é a força elástica em Newtons.
- k é a constante elástica em N/m.
- x é a deformação da mola ou o quanto ela esticou ou comprimiu.
Observe que o gráfico dessa questão fornece o Comprimento Total (L), não a deformação da mola.
A deformação (x) é calculada pela diferença entre o comprimento final e o comprimento inicial ou natural da mola, quando ela não está sujeita a nenhuma força, ou:
x = L − L0.
Identificando o Comprimento Inicial (L0).
Observe o gráfico no ponto onde a reta encontra o eixo x, nesse ponto a força é 0 N, então a mola não está deformada (esticada ou comprimida), possuindo o tamanho natural ou inicial.
Portanto, o comprimento natural da mola (L0) é 10 cm = 0,1 m.
O outro ponto mostrado no gráfico é o ponto (25 cm, 30N) que diz que o comprimento total da mola é igual a 25 cm quando a força elástica é de 30 N.
Vamos usar esses dados, para determinar a constante elástica da mola k, usando a Lei de Hooke:
- Fel = 30 N
- Comprimento Total L = 25 cm = 0,25 m
Para tanto temos que calcular a deformação x para este ponto:
x= 0,25 m − 0,10 m = 0,15 m
Agora podemos aplicar a Lei de Hooke:
Fel = k . x
30 = k . 0,15
k = 30 / 0,15 = 200 N/m
Vamos agora calcular o comprimento da mola para uma força de 50 N. Vamos usar novamente a Lei de Hooke, usando k = 200 N/m. Temos:
Fel = k . x
50 = 200 . x
x = 50 / 200 = 0,25 m = 25 cm
Agora lembre que a questão pede o comprimento total, não a deformação da mola. Assim temos que somar o tamanho inicial da mola à deformação encontrada de 25cm, ou:
Lfinal = L0 + x
Lfinal = 10 cm + 25 cm = 35 cm
Estude mais sobre força elástica e faça também exercícios sobre força de tração.
SOUTO, Ana. Exercícios sobre a força elástica (com gabarito explicado). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-a-forca-elastica-com-gabarito-explicado/. Acesso em:


