Acelere seus estudos para o ENEM: conheça o Toda Matéria+

Acelere seu aprendizado

ASSINAR TM +

Busque um tema

Língua Portuguesa
Matemática
História
Inglês
Geografia
Mais Matérias
Exercícios

ENEM 2025
Ajudante de Dever de CasaNOVO

Toda Matéria
Enem
›
Matemática e suas Tecnologias

Questões de Matemática no Enem

Rafael C. Asth

Professor de Matemática e Física

Remover anúncios

Confira questões resolvidas das últimas edições do Enem com as respostas comentadas.

Mas antes de começar, lembre: estudar com provas anteriores é importante, mas aprender com explicações detalhadas faz toda a diferença. No Toda Matéria+, você acessa exercícios exclusivos no estilo do Enem, com gabarito comentado passo a passo por professores especialistas, para entender o raciocínio por trás de cada questão.

Questão 1

(Enem 2022) Uma cozinheira produz docinhos especiais por encomenda. Usando uma receita-base de massa, ela prepara uma porção, com a qual produz 50 docinhos maciços de formato esférico, com 2 cm de diâmetro. Um cliente encomenda 150 desses docinhos, mas pede que cada um tenha formato esférico com 4 cm de diâmetro. A cozinheira pretende preparar o número exato de porções da receita-base de massa necessário para produzir os docinhos dessa encomenda.

Quantas porções da receita-base de massa ela deve preparar para atender esse cliente?

a) 2

b) 3

c) 6

d) 12

e) 24

Gabarito explicado

O volume total de receita-base é a multiplicação do volume de cada unidade, sendo esferas com 1 cm de raio, por 50 unidades.

Volume de uma unidade de doce é dado por:

$reto V igual a 4 sobre 3 reto pi reto r ao cuboreto V igual a 4 sobre 3 reto pi 1 ao cuboreto V igual a 4 sobre 3 reto pi$

Como são 50 unidade:

$50 espaço. espaço 4 sobre 3 reto pi espaço$

Pedido do cliente: 150 docinhos com 2 centímetros de raio.

O volume de uma unidade do novo docinho, é:

$reto V igual a 4 sobre 3 reto pi reto r ao cuboreto V igual a 4 sobre 3 reto pi 2 ao cuboreto V igual a 4 sobre 3 reto pi 8reto V igual a 32 sobre 3 reto pi$

Como são 150 docinhos:

$150 espaço. espaço 32 sobre 3 reto pi$

Número de receitas-base:

O número de receitas-base será o volume do pedido dividido pelo volume da receita-base.

$reto n igual a numerador volume espaço do espaço pedido sobre denominador volume espaço da espaço receita menos base fim da fraçãoreto n igual a numerador numerador 150 espaço. espaço 32 reto pi sobre denominador 3 fim da fração sobre denominador numerador 50 espaço. espaço 4 reto pi sobre denominador 3 fim da fração fim da fração igual a numerador 150 espaço. espaço 32 reto pi sobre denominador 3 fim da fração. numerador 3 sobre denominador 50 espaço. espaço 4 reto pi fim da fraçãoreto n igual a numerador riscado diagonal para cima sobre 150 ao cubo fim do riscado espaço. espaço 32 diagonal para cima risco reto pi sobre denominador diagonal para cima risco 3 fim da fração. numerador diagonal para cima risco 3 sobre denominador riscado diagonal para cima sobre 50 à potência de 1 fim do riscado espaço. espaço 4 diagonal para cima risco reto pi fim da fração igual a numerador 3.32 sobre denominador 4 fim da fração igual a 96 sobre 4 igual a 24$

Ainda com dúvidas? Pergunta ao Ajudante IA do Toda Matéria

Questão 2

Enem (2022) Ao escutar à notícia de que um filme recém-lançado arrecadou, no primeiro mês de lançamento, R$ 1,35 bilhão em bilheteria, um estudante escreveu corretamente o número que representa essa quantia, com todos os seus algarismos.

O número escrito pelo estudante foi

a) 135 000,00

b) 1 350 000,00

c) 13 500 000,00

d) 135 000 000,00

e) 1 350 000 000,00

Gabarito explicado

1,35 bilhão significa que a parte inteira, antes da vírgula, representa 1 unidade de bilhão. Assim, os números após a vírgula representam as ordens que vem logo em seguida, os milhões.

Basta completar as ordens e classes com zeros. Logo:

1 350 000 000,00

Questão 3

Uma montadora de automóveis divulgou que oferta a seus clientes mais de 1 000 configurações diferentes de carro, variando o modelo, a motorização, os opcionais e a cor do veículo. Atualmente, ela oferece 7 modelos de carros com 2 tipos de motores: 1.0 e 1.6. Já em relação aos opcionais, existem 3 escolhas possíveis: central multimídia, rodas de liga leve e bancos de couro, podendo o cliente optar por incluir um, dois, três ou nenhum dos opcionais disponíveis.

Para ser fiel à divulgação feita, a quantidade mínima de cores que a montadora deverá disponibilizar a seus clientes é

a) 8.

b) 9.

c) 11.

d) 18.

e) 24.

Gabarito explicado

Pelo princípio multiplicativo:

modelos de carros x tipos de motores x opcionais x cores $maior que ou igual a inclinado$ 1000

Entre os opcionais:

Escolher nenhum (1 possibilidade) ou;
Escolher um (3 possibilidades) ou;
Escolher dois (3 possibilidades);
- banco e multimídia
- banco e rodas
- multimídia e rodas, ou
Escolher três (1 possibilidade).

banco e multimídia
banco e rodas
multimídia e rodas, ou

Entre os opcionais utilizamos o princípio aditivo, logo:

1 + 3 + 3 + 1 = 8

Aplicando os valores conhecidos na inequação inicial e nomeando o número de cores por cm temos:

$modelos espaço de espaço carros espaço reto x espaço tipos espaço de espaço motores espaço reto x espaço opcionais espaço reto x espaço cores espaço 10007 espaço reto x espaço 2 espaço reto x espaço 8 espaço reto x espaço reto c espaço maior que ou igual a inclinado 1000112 reto c espaço maior que ou igual a inclinado 1000reto c espaço maior que ou igual a inclinado 1000 sobre 112reto c espaço maior que ou igual a inclinado 8 vírgula 92 espaço$

Desta forma, o número mínimo de cores que devem ser disponibilizadas é 9.

Questão 4

Uma máquina em operação tem sua temperatura T monitorada por meio de um registro gráfico, ao longo do tempo t. Essa máquina possui um pistão cuja velocidade V varia com a temperatura T da máquina, de acordo com à expressão V = T² - 4. Após a máquina funcionar durante o intervalo de tempo de 10 horas, o seu operador analisa o registro gráfico, apresentado na figura, para avaliar à necessidade de eventuais ajustes, sabendo que a máquina apresenta falhas de funcionamento quando a velocidade do pistão se anula.

Quantas vezes a velocidade do pistão se anulou durante as 10 horas de funcionamento?

a) 1.

b) 2.

c) 3.

d) 4.

e) 5.

Gabarito explicado

A velocidade do pistão se relaciona com a temperatura conforme a função:

V = T² - 4

Fazendo V igual a zero determinamos as temperaturas onde a velocidade se anula.

$reto V espaço igual a espaço reto T ² espaço menos espaço 40 espaço igual a espaço reto T ² espaço menos espaço 44 espaço igual a espaço reto T ²raiz quadrada de 4 espaço igual a reto Tmais ou menos 2$

Do gráfico, obtemos que a temperatura esteve em 2 ou -2 °C cinco vezes.

Questão 5

Uma das informações que pode auxiliar no dimensionamento do número de pediatras que devem atender em uma Unidade Básica de Saúde (UBS) é o número que representa a mediana da quantidade de crianças por família existente na região sob sua responsabilidade. O quadro mostra a distribuição das frequências do número de crianças por família na região de responsabilidade de uma UBS.

O número que representa a mediana da quantidade de crianças por família nessa região é

a) 1,0.

b) 1,5.

c) 1,9.

d) 2,1.

e) 2,5.

Gabarito explicado

Somando as frequências temos:

100 + 400 + 200 + 150 + 100 + 50 = 1000

Como o número de elementos é par, a mediana será a média aritmética entre os dois termos centrais, tempo organizado os dados de forma crescente.

Os termos centrais serão as posição 500 e 501.

Da tabela temos que o número de crianças por família na posição 500 é 1, enquanto para 501 é 2.

A mediana é:

$numerador 1 espaço mais espaço 2 sobre denominador 2 fim da fração espaço igual a 3 sobre 2 igual a 1 vírgula 5$

Acertar uma questão do Enem vai muito além de chutar a alternativa certa. Com o Toda Matéria+, você treina com exercícios exclusivos criados por professores especialistas em Enem, com resolução completa, explicada passo a passo, mostrando como pensar como a banca.

Questão 6

(Enem 2020). A Pesquisa Nacional por Amostra de Domicílios (Pnad) é uma pesquisa feita anualmente pelo IBGE, exceto nos anos em que há Censo. Em um ano, foram entrevistados 363 mil jovens para fazer um levantamento sobre suas atividades profissionais e/ou acadêmicas. Os resultados da pesquisa estão indicados no gráfico.

Remover anúncios

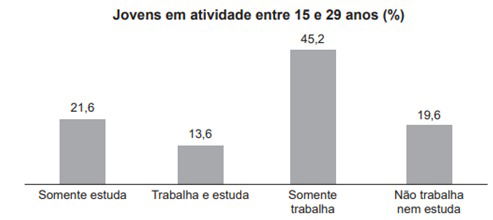
De acordo com as informações dadas, o número de jovens entrevistados que trabalha é

a) 114 708.
b) 164 076.
c) 213 444.
d) 284 592.
e) 291 582.

Ver Resposta

Resposta correta: c) 213 444.

Dado: número total de entrevistados: 363 000.

Ideia 1: percentual dos que trabalham.

Trabalha e estuda = 13,6%
Somente trabalha = 45,2%

Total que trabalham = 13,6 + 45,2 = 58,8%

Ideia 2: 58,8% de 363 000.

$58 vírgula 8 espaço sinal de percentagem espaço d e espaço 363 espaço 000 espaço espaço numerador 58 vírgula 8 sobre denominador 100 fim da fração espaço d e espaço 363 espaço 000 espaço espaço numerador 588 sobre denominador 1 espaço 000 fim da fração espaço sinal de multiplicação espaço 363 espaço 000 espaço espaço 588 espaço sinal de multiplicação espaço numerador 363 espaço 000 espaço sobre denominador 1 espaço 000 fim da fração 588 espaço sinal de multiplicação espaço 363 espaço espaço 213.444$

Portanto, o número de jovens entrevistados que trabalha é 213 444.

Questão 7

(Enem 2020). Para chegar à universidade, um estudante utiliza um metrô e, depois, tem duas opções:

• seguir num ônibus, percorrendo 2,0 km;
• alugar uma bicicleta, ao lado da estação do metrô, seguindo 3,0 km pela ciclovia.

O quadro fornece as velocidades médias do ônibus e da bicicleta, em km/h, no trajeto metrô−universidade.

A fim de poupar tempo no deslocamento para a universidade, em quais dias o aluno deve seguir pela ciclovia?

a) Às segundas, quintas e sextas-feiras.
b) Às terças e quintas-feiras e aos sábados.
c) Às segundas, quartas e sextas-feiras.
d) Às terças, quartas e sextas-feiras.
e) Às terças e quartas-feiras e aos sábados.

Ver Resposta

Resposta correta: c) Às segundas, quartas e sextas-feiras.

Interpretação e dados

Para saber em quais dias a bicicleta é mais rápida, é preciso fazer a comparação dia-a-dia.
É preciso calcular o tempo dia após dia, para cada veículo, pois o que a tabela fornece é a velocidade em km/h.

Distâncias percorridas:
2,0 Km de ônibus.
3,0 Km de bicicleta.

Velocidade é a distância percorrida em um intervalo de tempo.

$v e l o c i d a d e espaço igual a espaço numerador d i s t â n c i a sobre denominador espaço t e m p o fim da fração$

Assim, temos que:

$t e m p o espaço igual a espaço numerador d i s t â n c i a espaço sobre denominador v e l o c i d a d e fim da fração$

Comparação das frações de tempo

segunda-feira

$ô n i b u s espaço espaço espaço espaço espaço espaço b i c i c l e t a espaço espaço espaço espaço 2 sobre 9 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 3 sobre 15$

Igualando os denominadores: para isso, o denominador de cada fração multiplica o numerador e o denominador da outra fração.

$ô n i b u s espaço espaço espaço espaço espaço espaço espaço espaço espaço b i c i c l e t a numerador 2 sinal de multiplicação 15 sobre denominador 9 sinal de multiplicação 15 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 9 sinal de multiplicação espaço 3 sobre denominador 9 sinal de multiplicação 15 fim da fração$

Com os denominadores iguais, basta comparar os numeradores.

$ô n i b u s espaço espaço espaço espaço espaço espaço espaço espaço espaço b i c i c l e t a numerador 30 sobre denominador 9 sinal de multiplicação 15 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 27 sobre denominador 9 sinal de multiplicação 15 fim da fração$

Como 27 < 30, na segunda-feira o aluno deve seguir pela ciclovia.

Repetindo o mesmo raciocínio e cálculo para os outros dias da semana.

terça-feira

$espaço ô n i b u s espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço b i c i c l e t a espaço espaço espaço espaço 2 sobre 20 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 3 sobre 22 numerador 2 espaço sinal de multiplicação espaço 22 sobre denominador 20 espaço sinal de multiplicação espaço 22 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 20 espaço sinal de multiplicação espaço 3 sobre denominador 20 espaço sinal de multiplicação espaço 22 fim da fração numerador 44 sobre denominador 20 espaço sinal de multiplicação espaço 22 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 60 sobre denominador 20 espaço sinal de multiplicação espaço 22 fim da fração$

Assim, na terça-feira o ônibus é mais rápido.

quarta-feira

$espaço espaço ô n i b u s espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço b i c i c l e t a espaço espaço espaço espaço 2 sobre 15 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 3 sobre 24 numerador 2 espaço sinal de multiplicação espaço 24 sobre denominador 15 espaço sinal de multiplicação 24 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 15 espaço sinal de multiplicação espaço 3 sobre denominador 15 espaço sinal de multiplicação espaço 24 fim da fração numerador 48 sobre denominador 15 espaço sinal de multiplicação espaço 24 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 45 sobre denominador 15 espaço sinal de multiplicação espaço 24 fim da fração$

Na quarta-feira, a bicicleta é mais rápida.

quinta-feira

$espaço espaço ô n i b u s espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço b i c i c l e t a espaço espaço espaço espaço espaço 2 sobre 12 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador espaço 3 sobre denominador 15 fim da fração numerador 2 espaço sinal de multiplicação espaço 15 sobre denominador 12 espaço sinal de multiplicação espaço 15 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço numerador 3 espaço sinal de multiplicação espaço 12 sobre denominador 12 espaço sinal de multiplicação espaço 15 fim da fração numerador 30 sobre denominador 12 espaço sinal de multiplicação espaço 15 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço numerador 36 sobre denominador 12 espaço sinal de multiplicação espaço 15 fim da fração$

Na quinta-feira, o ônibus é mais rápido.

sexta-feira

$espaço espaço ô n i b u s espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço b i c i c l e t a espaço espaço espaço espaço espaço espaço 2 sobre 10 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 3 sobre 18 numerador 2 espaço sinal de multiplicação espaço 18 sobre denominador 10 espaço sinal de multiplicação espaço 18 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 10 espaço sinal de multiplicação espaço 3 sobre denominador 10 espaço sinal de multiplicação espaço 18 fim da fração espaço numerador 36 sobre denominador 10 espaço sinal de multiplicação espaço 18 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 30 sobre denominador 10 espaço sinal de multiplicação espaço 18 fim da fração$

Na sexta-feira a bicicleta é mais rápida.

sábado

$espaço espaço ô n i b u s espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço b i c i c l e t a espaço espaço espaço espaço espaço 2 sobre 30 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço 3 sobre 16 numerador 2 espaço sinal de multiplicação espaço 16 sobre denominador 30 espaço sinal de multiplicação espaço 16 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 30 espaço sinal de multiplicação espaço 3 sobre denominador 30 espaço sinal de multiplicação espaço 16 fim da fração numerador 32 sobre denominador 30 espaço sinal de multiplicação espaço 16 fim da fração espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço numerador 30 espaço sinal de multiplicação espaço 3 sobre denominador 30 espaço sinal de multiplicação espaço 16 fim da fração$

Assim, a bicicleta será mais eficiente às segundas, quartas e sextas-feiras.

Questão 8

(Enem 2020). Pesquisadores da Universidade de Tecnologia de Viena, na Áustria, produziram miniaturas de objetos em impressoras 3D de alta precisão. Ao serem ativadas, tais impressoras lançam feixes de laser sobre um tipo de resina, esculpindo o objeto desejado. O produto final da impressão é uma escultura microscópica de três dimensões, como visto na imagem ampliada.

A escultura apresentada é uma miniatura de um carro de Fórmula 1, com 100 micrômetros de comprimento. Um micrômetro é a milionésima parte de um metro. Usando notação científica, qual é a representação do comprimento dessa miniatura, em metro?

$a parêntese direito espaço 1 vírgula 0 espaço sinal de multiplicação espaço 10 à potência de menos 1 fim do exponencial espaço espaço espaço b parêntese direito espaço 1 vírgula 0 espaço sinal de multiplicação espaço 10 à potência de menos espaço 3 fim do exponencial espaço espaço espaço c parêntese direito espaço 1 vírgula 0 espaço sinal de multiplicação espaço 10 à potência de menos espaço 4 fim do exponencial espaço espaço espaço d parêntese direito espaço 1 vírgula 0 espaço sinal de multiplicação espaço 10 à potência de menos espaço 6 fim do exponencial espaço espaço espaço espaço e parêntese direito espaço 1 vírgula 0 espaço sinal de multiplicação espaço 10 à potência de menos espaço 7 fim do exponencial espaço$

Ver Resposta

Resposta correta: c) $1 vírgula 0 espaço sinal de multiplicação espaço 10 à potência de menos espaço 4 fim do exponencial espaço$

Objetivo: escrever o número 100 micrômetros em metro, usando notação científica.

1 micrômetro = 1 m / 1 000 000

Multiplicando por 100 ambos os lados da equação.

1 micrômetros x 100 = 1 m x 100 / 1 000 000

100 micrômetros = 1 m / 10 000

100 micrômetros = 0,0001 m

Escrevendo em notação científica.

Para escrever em notação científica, deixamos um algarismo na parte inteira, antes da vírgula e escrevemos a potência de base 10.

$0 vírgula 0001 igual a 1 vírgula 0 espaço sinal de multiplicação espaço 10 à potência de menos 4 fim do exponencial$

Como deslocamos a vírgula para direita, aumentando o número, compensamos com o expoente negativo na potência de base 10.

Portanto, $100 espaço m i c r ô m e t r o s igual a 1 vírgula 0 espaço x espaço 10 à potência de menos 4 fim do exponencial espaço m.$

Remover anúncios

Questão 9

(Enem 2020). Uma empresa de ônibus utiliza um sistema de vendas de passagens que fornece a imagem de todos os assentos do ônibus, diferenciando os assentos já vendidos, por uma cor mais escura, dos assentos ainda disponíveis. A empresa monitora, permanentemente, o número de assentos já vendidos e compara-o com o número total de assentos do ônibus para avaliar a necessidade de alocação de veículos extras. Na imagem tem-se a informação dos assentos já vendidos e dos ainda disponíveis em um determinado instante.

A razão entre o número de assentos já vendidos e o total de assentos desse ônibus, no instante considerado na imagem, é

a) 16/42
b) 16/26
c) 26/42
d) 42/26
e) 42/16

Ver Resposta

Resposta correta: a) 16/42

Razão é uma divisão na forma de uma fração e estamos em busca da seguinte razão:

$numerador n ú m e r o espaço d e espaço a s s e n t o s espaço v e n d i d o s sobre denominador n ú m e r o espaço t o t a l espaço d e espaço a s s e n t o s fim da fração$

De acordo com a imagem, temos:

16 vendidos em um total de 42 lugares. Por isso, a razão procurada é 16/42.

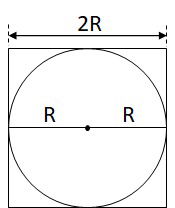
Questão 10

A caixa-d’água de um edifício terá a forma de um paralelepípedo retângulo reto com volume igual a 28 080 litros. Em uma maquete que representa o edifício, a caixa-d’água tem dimensões 2 cm × 3,51 cm × 4 cm.

Dado: 1 dm³ = 1 L.

A escala usada pelo arquiteto foi

a) 1 : 10
b) 1 : 100
c) 1 : 1 000
d) 1 : 10 000
e) 1 : 100 000

Ver Resposta

Resposta correta: b) 1 : 100

Ideia 1
O enunciado pergunta a escala das medidas lineares. Queremos determinar quantos centímetros de comprimento a caixa real possui para cada 1 centímetro da maquete. Ou seja:

$numerador 1 espaço sobre denominador D fim da fração$

Onde D representa uma medida de 1 dimensão.

Ideia 2
Primeiro, vamos determinar a escala dos volumes que são quantos cm³ a caixa real possui para cada 1 cm³ a maquete possui.

$1 sobre D ao cubo$

Onde D³ representa uma medida de 3 dimensões, ou seja, de volume.

Ideia 3

Por fim, convertemos de cm³ para dm³ e, assim, pala litros. Uma vez determinado a quantidade de líquido na maquete, fazemos a razão da escala comparando com a caixa real.

Passo 1: volume da maquete

Volume = comprimento x largura x altura
Como é um produto, a ordem não altera o resultado.

Volume = 2 x 3,51 x 4 = 28,08 cm³

Passo 2: passando de cm³ para dm³

1 dm³ = 10 cm x 10 cm x 10 cm = 1 000 cm³

Fazendo uma regra de três

Se 1 000 cm³ é igual a 1 dm³, então 28,08 cm³ será igual a x dm³ .

$numerador 1 espaço d m ³ sobre denominador 1 espaço 000 espaço c m ³ espaço fim da fração igual a espaço numerador x espaço d m ³ sobre denominador 28 vírgula 08 espaço c m ³ fim da fração$

1000 . x = 28,08 x 1
x = 28,08 / 1000
x = 0,02808 dm³

Passo 3: decímetros cúbicos para litros

Se 1 dm³ equivale a 1 litro, então 0,02808 dm³ será igual a 0,02808 L.
Dessa forma, 0,02808 L é a capacidade da maquete.

Passo 4: razão dos volumes

$numerador V o l u m e espaço r e a l sobre denominador v o l u m e espaço d a espaço m a q u e t e fim da fração espaço igual a espaço numerador 28080 sobre denominador 0 vírgula 02808 fim da fração espaço igual a espaço 1 espaço 000 espaço 000$

Passo 5: a escala de volume 1 / D³

$numerador 1 sobre denominador v o l u m e fim da fração igual a numerador 1 sobre denominador 1 espaço 000 espaço 000 fim da fração$

Como o volume é espacial, possuindo três dimensões, fazemos volume igual a D³.

$1 sobre D ao cubo igual a numerador 1 sobre denominador 1 espaço 000 espaço 000 fim da fração$

Passo 6: a escala linear 1 / D

Multiplicando cruzado

$1 sobre D ao cubo igual a numerador 1 sobre denominador 1 espaço 000 espaço 000 fim da fração$

$D ao cubo igual a 1 espaço 000 espaço 000 D igual a cúbica raiz de 1 espaço 000 espaço 000 fim da raiz D espaço igual a espaço 100 espaço$

Logo, a escala procurada é 1/100

Questão 11

(Enem 2020). Um processo de aeração, que consiste na introdução de ar num líquido, acontece do seguinte modo: uma bomba B retira o líquido de um tanque T1 e o faz passar pelo aerador A1, que aumenta o volume do líquido em 15%, e em seguida pelo aerador A2, ganhando novo aumento de volume de 10%. Ao final, ele fica armazenado num tanque T2, de acordo com a figura.

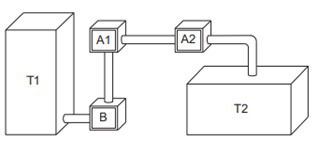
Os tanques T1 e T2 são prismas retos de bases retangulares, sendo que a base de T1 tem comprimento c e largura L, e a base de T2 tem comprimento c/2 e largura 2L.

Para finalizar o processo de aeração sem derramamento do líquido em T2, o responsável deve saber a relação entre a altura da coluna de líquido que já saiu de T1, denotada por X, e a altura da coluna de líquido que chegou a T2, denotada por y.

A equação que relaciona as medidas das alturas y e x é dada por

a) y = 1,265x
b) y = 1,250x
c) y = 1,150x
d) y = 1,125x
e) y = x

Ver Resposta

Resposta correta: a) y = 1,265x

Temas cobrados nesta questão: porcentagem e geometria espacial.

Ideia 1: alteração percentual de volume do tanque T1 para o T2.

O volume V2, do tanque T2 é maior, pois sofreu processo de aeração.

Em A1 o volume aumenta 15%. Basta multiplicar por 1,15.
Em A2 o volume aumenta mais 10%. Basta multiplicar por 1,10.

Ideia 2: relação entre os volumes

Caso não sofresse aeração, o volume de líquido V1, que sai de T1, seria igual ao volume V2 em T2.

Como o volume final, V2, é maior devido aos aumentos, temos:

V2 = (1,15 )(1,10) . V1
V2 = 1,265 . V1 relação I

Ideia 3: função dos volumes

Como os tanques são prismas, o volume é o resultado da multiplicação de suas três dimensões.

Substituindo o produto na relação I, temos:

V2 = 1,265 . V1 relação I

$y espaço. espaço C sobre 2 espaço. espaço 2 L espaço igual a espaço 1 vírgula 265 espaço. espaço x espaço. espaço C. espaço L espaço espaço y espaço. espaço C espaço. espaço L espaço igual a espaço 1 vírgula 265 espaço. espaço x espaço. espaço C espaço. espaço L espaço espaço y espaço igual a espaço 1 vírgula 265 espaço. espaço x espaço. espaço numerador C espaço. espaço L sobre denominador C espaço. espaço L fim da fração espaço espaço y espaço igual a espaço 1 vírgula 265 espaço x$

Portanto, a equação que relaciona as medidas das alturas y e x é dada por y = 1,265 x

Questão 12

(Enem 2020). A fabricação da Bandeira Nacional deve obedecer ao descrito na Lei n. 5.700, de 1º de setembro de 1971, que trata dos Símbolos Nacionais. No artigo que se refere às dimensões da Bandeira, observa-se: “Para cálculos das dimensões, será tomada por base a largura, dividindo-a em 14 (quatorze) partes iguais, sendo que cada uma das partes será considerada uma medida ou módulo (M). Os demais requisitos dimensionais seguem o critério abaixo:

Remover anúncios

I. Comprimento será de vinte módulos (20 M);

II. A distância dos vértices do losango amarelo ao quadro externo será de um módulo e sete décimos (1,7 M);

III. O raio do círculo azul no meio do losango amarelo será de três módulos e meio (3,5 M).”

BRASIL. Lei n. 5.700, de 1º de setembro de 1971.Disponível em: www.planalto.gov.br. Acesso em: 15 set. 2015.

A figura indica as cores da bandeira do Brasil e localiza o quadro externo a que se refere a Lei n. 5.700.

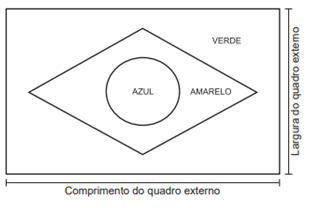
Um torcedor, preparando-se para a Copa do Mundo e dispondo de cortes de tecidos verde (180 cm x 150 cm) e amarelo (o quanto baste), deseja confeccionar a maior Bandeira Nacional possível a partir das medidas do tecido verde.

Qual a medida, em centímetro, do lado do menor quadrado de tecido azul que deverá ser comprado para confecção do círculo da bandeira desejada?

a) 27
b) 32
c) 53
d) 63
e) 90

Ver Resposta

Resposta correta: d) 63

Ideia 1: lado do quadrado

O lado do menor quadrado de tecido azul é igual a dois raios do círculo.

De acordo com a norma citada no enunciado em III, o raio R do círculo tem 3,5M.

Como o lado do quadrado é igual a 2R, temos:

Lado do quadrado = 2R = 2 . 3,5M = 7M

Ideia 2: cálculo de M em duas tentativas

O tecido verde é um retângulo e possui as dimensões: 180 cm X 150 cm.
De acordo com a norma, em I, o comprimento deve possuir 20M e a largura 14M.

1ª tentativa

Vamos utilizar o menor lado do tecido (150 cm) para o menor lado da bandeira (largura).

Largura da bandeira = 14M

Se a largura for de 150 cm, M será:

14M = 150 cm
M = 150/14

Devemos conferir se a medida maior do tecido (180 cm) será suficiente para o comprimento de 20M da bandeira.

Largura = 20M = 20. 150/14
Ou, aproximadamente, 214 cm, que é uma medida maior que a do tecido disponível.

2ª tentativa

Comprimento da bandeira de 20M com 180 cm.

20M = 180
M = 180/20 = 9 cm

Largura da bandeira = 14M
Largura da bandeira = 14 x 9 = 126 cm

Nesse caso, haverá tecido suficiente.

Ideia 3: medida do lado do quadrado

Como visto na ideia 1, o lado do quadrado possui 7M. Dessa forma:

Lado do quadrado = 7M = 7.9 = 63

Portanto, o lado do menor quadrado de tecido azul que deverá ser comprado para confecção do círculo da bandeira deve medir 63 cm.

Questão 13

(Enem 2020). Nos livros Harry Potter, um anagrama do nome do personagem “TOM MARVOLO RIDDLE” gerou a frase “I AM LORD VOLDEMORT”.

Suponha que Harry quisesse formar todos os anagramas da frase “I AM POTTER”, de tal forma que as vogais e consoantes aparecessem sempre intercaladas, e sem considerar o espaçamento entre as letras.

Nessas condições, o número de anagramas formados é dado por

a) 9!
b) 4! 5!
c) 2 × 4! 5!
d) 9! / 2
e) 4! 5! / 2

Ver Resposta

Resposta correta: e) 4! 5! / 2

Assunto cobrado na questão: permutação com repetição.

Na frase I AM POTTER, a letra T se repete duas vezes, sendo um caso de permutação com repetição.

Atenção: por ser uma permutação com repetição, devemos dividir o cálculo por 2! Pois a letra T se repete duas vezes.

Condição: vogais (V) e consoantes (C) devem estar intercaladas.

Na frase há 4 vogais e 5 consoantes.

Vamos considerar o caso em que começamos a dispor as letras, sendo a primeira vogal.

Esse caso não satisfaz a condição de vogais e consoantes intercaladas.

Agora, começando por consoante.

Esse caso satisfaz a condição.

Para as consoantes temos o seguinte produto de possibilidades:

5 possibilidades para escolher a primeira consoante, multiplicado por
4 possibilidades para escolher a segunda consoante, multiplicado por
3 possibilidades para escolher a terceira consoante, multiplicado por
2 possibilidades para escolher a quarta consoante, multiplicado por
1 possibilidade para escolher a quinta consoante.

Dessa forma, temos 5! que é o fatorial de 5.

Para as vogais temos o seguinte produto de possibilidades:

4 possibilidades para escolher a primeira vogal, multiplicado por
3 possibilidades para escolher a segunda vogal, multiplicado por
2 possibilidades para escolher a terceira vogal, multiplicado por
1 possibilidade para escolher a quarta vogal.

Dessa forma, temos 4! que é o fatorial de 4.

A quantidade total de anagramas é dada por:

Possibilidades das consoantes (5!), multiplicado pelas possibilidades das vogais (4!), dividido por 2! pois T se repete duas vezes.

$numerador V fatorial sinal de multiplicação C fatorial sobre denominador 2 fatorial fim da fração espaço$

Portanto, o número de anagramas formados é dado por:

$numerador 4 fatorial espaço 5 fatorial sobre denominador 2 fatorial fim da fração espaço$

Questão 14

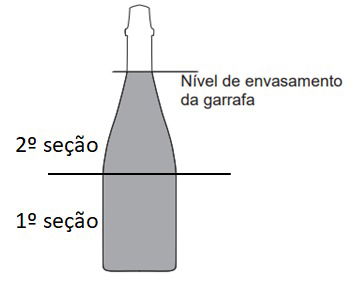
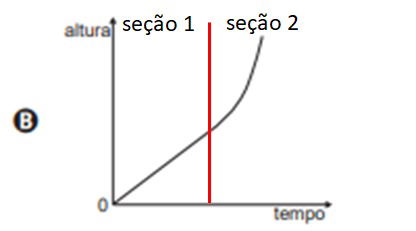
(Enem 2020). O consumo de espumantes no Brasil tem aumentado nos últimos anos. Uma das etapas do seu processo de produção consiste no envasamento da bebida em garrafas semelhantes às da imagem. Nesse processo, a vazão do líquido no interior da garrafa é constante e cessa quando atinge o nível de envasamento.

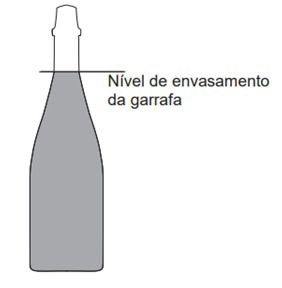
Qual esboço de gráfico melhor representa a variação da altura do líquido em função do tempo, na garrafa indicada na imagem?

Remover anúncios

Ver Resposta

Resposta correta: b)

Informação: a vazão é constante.

A vazão é a quantidade de líquido que entra na garrafa por unidade de tempo.

Por exemplo, a quantidade de líquido que entra na garrafa em 1 segundo, é a mesma, que entra no próximo segundo, e assim por diante.

Se o recipiente for grande como uma caixa d’água, o nível de líquido vai subir mais devagar. Dizemos que demora mais para encher uma caixa d’água do que uma garrafa pois o volume da garrafa é menor.

Com a garrafa é o mesmo princípio. Dividindo a garrafa em duas seções temos:

1ª seção

Na primeira seção o volume é maior, sendo um cilindro, sua circunferência é a mesma em toda altura. Como a vazão é constante, o gráfico da altura do nível em função do tempo é uma reta com inclinação que depende da vazão.

Se a vazão for maior, a garrafa se enche em menos tempos e, a inclinação da reta é maior.

2ª seção

Na segunda seção o volume (espaço dentro da garrafa) começa a diminuir. Conforme a altura do líquido aumenta a circunferência diminui e com isso o volume também diminui.

Sendo a vazão constante mas, o volume a ser preenchido cada vez menor, a medida que a altura aumenta, mais rápido é o preenchimento, ou seja, em menor tempo.

Questão 15

(Enem 2020). A exposição a barulhos excessivos, como os que percebemos em geral em trânsitos intensos, casas noturnas e espetáculos musicais, podem provocar insônia, estresse, infarto, perda de audição, entre outras enfermidades. De acordo com a Organização Mundial da Saúde, todo e qualquer som que ultrapasse os 55 decibéis (unidade de intensidade do som) já pode ser considerado nocivo para a saúde. O gráfico foi elaborado a partir da medição do ruído produzido, durante um dia, em um canteiro de obras.

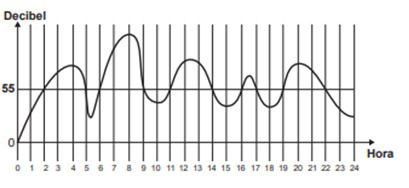
Nesse dia, durante quantas horas o ruído esteve acima de 55 decibéis?

a) 5
b) 8
c) 10
d) 11
e) 13

Ver Resposta

Resposta correta: e) 13

O ruído esteve acima de 55 dB nos períodos em que a curva do gráfico se mantém acima da linha horizontal de 55 dB.

Fazendo a contagem no gráfico, temos:

Horas em que o ruído esteve acima de 55 decibéis

3h + 3h + 3h + 1h + 3h = 13h

Portanto, neste dia, o ruído esteve por 13h acima do nível de 55 dB.

Questão 16

(Enem 2020). Os gráficos representam a produção de peças em uma indústria e as horas trabalhadas dos funcionários no período de cinco dias. Em cada dia, o gerente de produção aplica uma metodologia diferente de trabalho. Seu objetivo é avaliar a metodologia mais eficiente para utilizá-la como modelo nos próximos períodos. Sabe-se que, neste caso, quanto maior for a razão entre o número de peças produzidas e o número de horas trabalhadas, maior será a eficiência da metodologia.

Em qual dia foi aplicada a metodologia mais eficiente?

a) 1
b) 2
c) 3
d) 4
e) 5

Ver Resposta

Resposta correta: c) 3

A razão será:

$numerador n ú m e r o espaço d e espaço p e ç a s espaço p r o d u z i d a s sobre denominador n ú m e r o espaço d e espaço h o r a s espaço t r a b a l h a d a s fim da fração$

Analisando as razões para cada dia, temos:

Dia 1
800 / 4 = 200

Dia 2
1000 / 8 = 125

Dia 3
1 100 / 5 = 220

Dia 4
1800 / 9 = 200

Dia 5
1400 / 10 = 140

Desta forma, a metodologia mais produtiva foi a aplicada no dia 3.

Questão 17

(Enem/2019) Em um determinado ano, os computadores da receita federal de um país identificaram como inconsistentes 20% das declarações de imposto de renda que lhe foram encaminhadas. Uma declaração é classificada como inconsistente quando apresenta algum tipo de erro ou conflito nas informações prestadas. Essas declarações consideradas inconsistentes foram analisadas pelos auditores, que constataram que 25% delas eram fraudulentas. Constatou-se ainda que, dentre as declarações que não apresentaram inconsistências, 6,25% eram fraudulentas.

Qual é a probabilidade de, nesse ano, a declaração de um contribuinte ser considerada inconsistente, dado que ela era fraudulenta?

a) 0,0500
b) 0,1000
c) 0,1125
d) 0,3125
e) 0,5000

Ver Resposta

Alternativa correta: e) 0,5000.

1º passo: determinar a porcentagem de declarações inconsistentes que apresentam fraudes.

A quantidade de declarações recebidas nesse ano pela receita federal não foi dada, mas segundo o enunciado 20% do total são inconsistentes. Da parcela de inconsistentes, 25% foram consideradas fraudulentas. Precisamos então calcular porcentagem de porcentagem, ou seja 25% de 20%.

$espaço espaço 25 sinal de percentagem espaço reto x espaço 20 sinal de percentagem espaço 25 sobre 100 espaço reto x espaço 20 sinal de percentagem espaço igual a espaço 5 sinal de percentagem$

2º passo: determinar a porcentagem de declarações consistentes que apresentam fraudes.

O restante das declarações, que representa 80%, foram consideradas consistentes. Entretanto, constatou-se que dessa parcela 6,25% eram fraudulentas, ou seja:

$espaço 6 vírgula 25 sinal de percentagem espaço reto x espaço 80 sinal de percentagem numerador 6 vírgula 25 sobre denominador 100 fim da fração espaço reto x espaço 80 sinal de percentagem espaço igual a espaço 5 sinal de percentagem$

3º passo: calcular a probabilidade de uma declaração ser inconsistente e apresentar fraude.

A probabilidade é dada por:

$reto P parêntese esquerdo reto A parêntese direito = numerador espaço reto n parêntese esquerdo reto A parêntese direito sobre denominador reto n parêntese esquerdo reto ómega maiúsculo parêntese direito fim da fração$

Onde, a probabilidade de ocorrer um evento, P(A), é dada pela razão entre número de casos que nos interessam, n(A), e o número total de casos possíveis, n( $reto ómega maiúsculo$ ).

$reto P espaço estreito igual a espaço numerador 5 sinal de percentagem sobre denominador 5 sinal de percentagem espaço mais espaço 5 sinal de percentagem fim da fração igual a espaço numerador 5 sinal de percentagem sobre denominador 10 sinal de percentagem fim da fração igual a espaço 50 sinal de percentagem$

Sendo assim, a probabilidade de uma declaração ser inconsistente e fraudulenta é de 50% ou 0,5000.

Questão 18

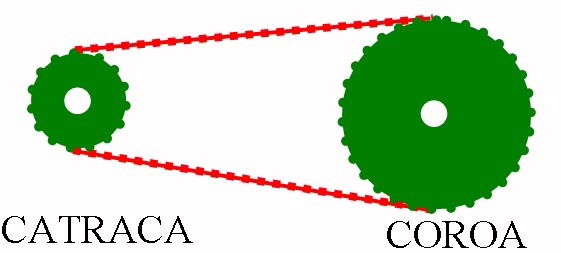
(Enem/2019) Um ciclista quer montar um sistema de marchas usando dois discos dentados na parte traseira de sua bicicleta, chamados catracas. A coroa é o disco dentado que é movimentado pelos pedais da bicicleta, sendo que a corrente transmite esse movimento às catracas, que ficam posicionadas na roda traseira da bicicleta. As diferentes marchas ficam definidas pelos diferentes diâmetros das catracas, que são medidos conforme indicação da figura.

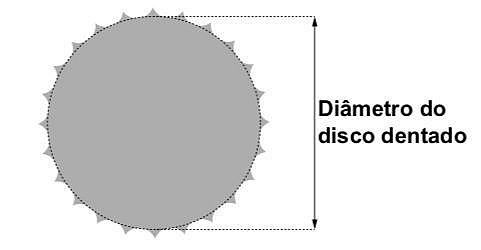
O ciclista já dispõe de uma catraca com 7 cm de diâmetro e pretende incluir uma segunda catraca, de modo que, à medida em que a corrente passe por ela, a bicicleta avance 50% a mais do que avançaria se a corrente passasse pela primeira catraca, a cada volta completa dos pedais.

O valor mais próximo da medida do diâmetro da segunda catraca, em centímetro e com uma casa decimal, é

a) 2,3
b) 3,5
c) 4,7
d) 5,3
e) 10,5

Remover anúncios

Ver Resposta

Alternativa correta: c) 4,7.

Observe como são posicionadas catraca e coroa na bicicleta.

Quando os pedais da bicicleta se movimentam, a coroa gira e o movimento é transmitido para catraca através da corrente.

Por ser menor, um giro da coroa faz com que a catraca realize mais voltas. Se, por exemplo, a catraca tiver um quarto do tamanho da coroa, significa que um giro da coroa fará com que a catraca gire quatro vezes mais.

Como a catraca está localizada na roda, quanto menor a catraca utilizada maior será a velocidade alcançada e, consequentemente, maior a distância percorrida. Por isso, diâmetro da catraca e distância percorrida são grandezas inversamente proporcionais.

Já foi escolhida uma de 7 cm e pretende-se avançar mais 50% com a bicicleta, ou seja, a distância percorrida (d) mais 0,5 d (que representa 50%). Logo, a nova distância que deve ser alcançada é de 1,5 d.

Distância percorrida	Diâmetro da catraca
d	7 cm
1,5 d	x

Já que a proporcionalidade entre as grandezas é inversa, devemos inverter a grandeza do diâmetro da catraca e efetuar o cálculo com a regra de três.

$tabela linha com reto d menos x blank linha com célula com 1 vírgula 5 espaço reto d fim da célula menos célula com 7 espaço cm fim da célula blank linha com blank blank blank blank linha com reto x igual a célula com numerador 7 espaço cm espaço. espaço diagonal para cima risco reto d sobre denominador 1 vírgula 5 espaço diagonal para cima risco reto d fim da fração fim da célula blank linha com reto x aproximadamente igual célula com 4 vírgula 7 fim da célula blank fim da tabela$

Como a roda e a catraca estão interligadas, o movimento realizado no pedal é transmitido para coroa e movimenta a catraca de 4,7 cm fazendo com que a bicicleta avance mais 50%.

Questão 19

(Enem/2019) Para construir uma piscina, cuja área total da superfície interna é igual a 40 m², uma construtora apresentou o seguinte orçamento:

R$ 10 000,00 pela elaboração do projeto;
R$ 40 000,00 pelos custos fixos;
R$ 2 500,00 por metro quadrado para construção da área interna da piscina.

Após a apresentação do orçamento, essa empresa decidiu reduzir o valor de elaboração do projeto em 50%, mas recalculou o valor do metro quadrado para a construção da área interna da piscina, concluindo haver a necessidade de aumentá-lo em 25%.

Além disso, a construtora pretende dar um desconto nos custos fixos, de maneira que o novo valor do orçamento seja reduzido em 10% em relação ao total inicial.

O percentual de desconto que a construtora deverá conceder nos custos fixos é de

a) 23,3%
b) 25,0%
c) 50,0%
d) 87,5%
e) 100,0%

Ver Resposta

Alternativa correta: d) 87,5%.

1º passo: calcular o valor inicial do investimento.

Orçamento	Valor
Elaboração do projeto	10 000,00
Custos fixos	40 000,00
Construção da área interna de 40 m² da piscina.	40 x 2 500,00

$10 espaço 000 espaço mais espaço 40 espaço 000 espaço mais espaço 100 espaço 000 espaço igual a espaço 150 espaço 000$

2º passo: Calcular o valor de elaboração do projeto após a redução de 50%

$10 espaço 000 espaço. espaço parêntese esquerdo 1 menos 0 vírgula 5 parêntese direito espaço igual a espaço 5 espaço 000$

3º passo: Calcular o valor do metro quadrado da piscina após aumento de 25%.

$100 espaço 000 espaço. espaço parêntese esquerdo 1 mais 0 vírgula 25 parêntese direito espaço igual a espaço 125 espaço 000$

4º passo: Calcular o desconto aplicado nos custos fixos para reduzir o valor do orçamento inicial em 10%.

$tabela linha com célula com Elaboração espaço fim da célula mais custos mais célula com metro espaço fim da célula igual a linha com célula com do espaço projeto fim da célula blank fixos blank quadrado blank linha com blank blank blank blank blank blank linha com célula com 5 espaço 000 fim da célula mais célula com 40 espaço 000. parêntese esquerdo 1 menos reto i parêntese direito fim da célula mais célula com 125 espaço 000 fim da célula igual a fim da tabela tabela linha com célula com valor espaço fim da célula linha com célula com do espaço investimento fim da célula linha com blank linha com célula com 150 espaço 000. parêntese esquerdo 1 menos 0 vírgula 1 parêntese direito fim da célula fim da tabela 1 menos espaço reto i espaço igual a espaço numerador 135 espaço 000 espaço menos espaço 5 espaço 000 espaço menos espaço 125 espaço 000 sobre denominador 40 espaço 000 fim da fração 1 menos espaço reto i espaço igual a 0 vírgula 125 espaço reto i espaço igual a espaço 1 espaço menos espaço 0 vírgula 125 espaço reto i espaço igual a 0 vírgula 875 espaço igual a espaço 87 vírgula 5 sinal de percentagem$

Com a aplicação dos 87,5% de desconto, os custos fixos passarão de R$ 40 000 para R$ 5 000 para que o valor final pago seja de R$ 135 000.

Ficar só nas provas antigas não basta. Com o Toda Matéria+, você estuda com exercícios inéditos organizados por tema, e cada questão vem com resolução detalhada, explicada por professores especialistas no estilo Enem. Você entende o porquê de cada passo, e aprende a pensar como a prova exige.

Questão 20

Conteúdo exclusivo para assinantes Toda Matéria+

Além de mais exercícios, tenha acesso a mais recursos para dar um up nos seus estudos.

Corretor de Redação para o Enem

Exercícios exclusivos

Estude sem publicidade

Assinar Toda Matéria+

Já é Toda Matéria+? Faça seu login

Não pare por aqui. Acreditamos que esses textos serão muito úteis nos seus estudos:

Matemática no Enem
Exercícios de Matemática Básica
Quiz Matemática e suas tecnologias
Quiz Ciências da Natureza e Suas Tecnologias
Simulado Enem: 20 questões que caíram na prova
- Questões Enem: 30 questões que caíram na prova

Este conteúdo foi útil?

sim

não

Obrigado. Como podemos melhorar ainda mais?

Como podemos melhorar?

Este conteúdo contém informação incorreta
Este conteúdo não tem a informação que procuro
Outro

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

ASTH, Rafael. Questões de Matemática no Enem. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/questoes-de-matematica-enem/. Acesso em:

Veja também