Condição de alinhamento de três pontos: aprenda a verificar (com exemplos)
Três pontos estão alinhados quando podem ser conectados por uma única reta no plano cartesiano.
Em outras palavras, se conseguirmos traçar uma reta que passe exatamente pelos três pontos, a condição para estarem alinhados é satisfeita e podemos afirmar que são colineares.
Com auxílio da Geometria Analítica, utilizamos métodos que nos garantem que três pontos estão alinhados.
Condições para que três pontos estejam alinhados
Existem diferentes formas de verificar se três pontos estão alinhados no plano cartesiano. Vamos explorar os principais métodos, lembrando que basta utilizar um deles.
Método do Determinante
Sejam três pontos ,
e
no plano cartesiano. Estes pontos estão alinhados se, e somente se, o determinante da seguinte matriz é igual a zero:
Condição de alinhamento:
-
Se Det = 0 → Pontos alinhados;
-
Se Det ≠ 0 → Pontos não alinhados (formam um triângulo).
Desenvolvendo este determinante:
Para calcular um determinante, você também pode utilizar a regra de Sarrus.
Exemplo: Verifique se os pontos A(1, 2), B(3, 4) e C(5, 6) estão alinhados.
x1 = 1; x2 = 3; x3 = 5;
y1 = 2; y2 = 4; y3 = 6.
Resolução: Aplicamos a fórmula do determinante:
A condição do determinante igual a zero foi satisfeita, logo, os pontos A, B e C estão alinhados.
Método do Coeficiente Angular
Três pontos estão alinhados quando os coeficientes angulares das retas que passam por quaisquer dois deles são iguais.
Se tivermos os pontos A(x1,y1), B(x2,y2) e C(x3,y3), podemos calcular:
Coeficiente angular da reta AB:
Coeficiente angular da reta BC:
Se , então os três pontos estão alinhados.
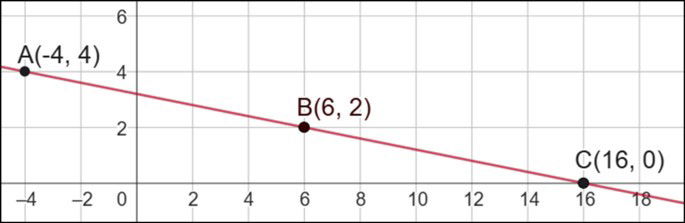
Exemplo: Verifique se os pontos A(1,2), B(3,6) e C(5,10) estão alinhados.
Calculando o coeficiente angular de AB:
Calculando o coeficiente angular de BC:
A condição de que os coeficientes angulares das retas que dão suporte a ambos os seguimentos serem iguais foi satisfeita, logo, os pontos são colineares. Acompanhe:
Método da equação da reta
Outra forma de verificar se três pontos pertencem a mesma reta é determinar a equação da reta que passa pelos pontos A e B, e verificar se o ponto C satisfaz esta equação.
A equação da reta no plano cartesiano pode ser apresentada de várias formas, vamos relembrar a forma reduzida:
Com m e n sendo números reais.
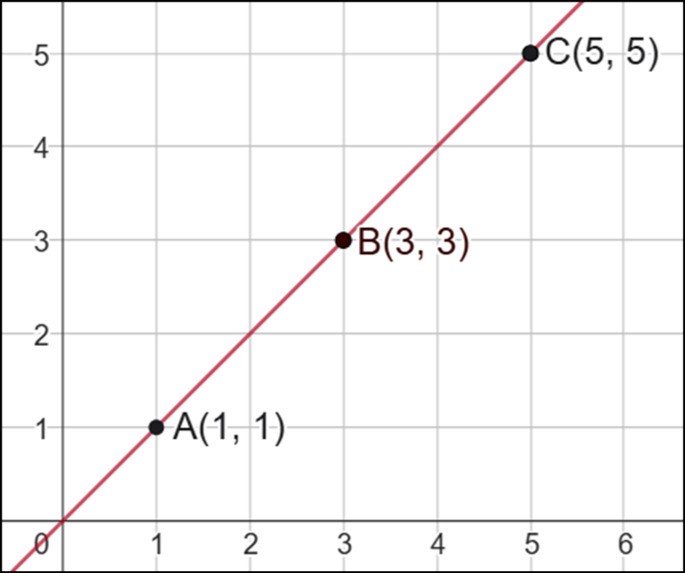
Exemplo: Verificar se os pontos A(1,1), B(3,3) e C(5,5) estão alinhados.
Vamos determinar a equação da reta que passa por A e B.
Primeiro calculamos o coeficiente angular:
Substituímos na equação da reta:
Para determinar n, substituímos os valores de x e y do ponto A ou B. Vamos utilizar o ponto A(1,1):
Logo, a equação da reta fica:
Por fim, testamos as coordenadas do ponto C(5,5):
De fato, é verdade que 5 = 5.
Como a condição das coordenadas de um terceiro ponto pertencerem à reta que dá suporte aos dois primeiros foi satisfeita, os três pontos estão alinhados.
Veja:
Exercícios sobre alinhamento de três pontos
Questão 1
Os pontos A(2, 1), B(4, 3) e C(8, 7) estão alinhados?
a) Sim, pois formam um triângulo equilátero.
b) Não, pois o determinante formado por suas coordenadas não é nulo.
c) Sim, pois o determinante formado por suas coordenadas é nulo.
d) Não, pois os coeficientes angulares das retas AB e BC são diferentes.
e) Não, pois formam um triângulo isósceles.
Explicação: Calculando o determinante:
x1 = 2; y1 = 1
x2 = 4; y2 = 3
x3 = 8; y3= 7
Resolvendo:
Como o determinante é zero, os pontos estão alinhados.
Questão 2
Determine o ponto P(x, 5) para que os pontos A(1, 2), B(3, 4) e P estejam alinhados.
a) P(5, 5)
b) P(4, 5)
c) P(6, 5)
d) P(5, 6)
e) P(1, 6)
Vamos aplicar a condição de alinhamento do determinante igual a zero.
x1 = x; y1 = 5
x2 = 1; y2 = 2
x3 = 3; y3 = 4
Logo, as coordenadas do ponto P são (4, 5).
Questão 3
Qual é o valor de y para que os pontos (1, 2), (3, 4) e (5, y) estejam alinhados?
a) 5
b) 6
c) 7
d) 8
e) 9
Podemos usar o coeficiente angular da reta que passa por (1, 2) e (3, 4):
Para que o terceiro ponto (5, y) esteja na mesma reta, o coeficiente angular entre (3, 4) e (5, y) deve ser igual a 1:
Portanto, a resposta correta é B.
Questão 4
Os pontos P(1,3), Q(2,5) e R(4,9) estão alinhados?
a) Sim, porque a soma das coordenadas é igual.
b) Não, porque formam um triângulo.
c) Sim, porque .
d) Não, porque o determinante é diferente de zero.
Vamos analisar as possibilidades:
a) Sim, porque a soma das coordenadas é igual.
Esta não é uma condição para os pontos estarem alinhados.
b) Não, porque formam um triângulo.
Formar um triângulo é uma consequência do não alinhamento dos pontos.
c) Sim, porque .
Coeficiente angular PQ:
Coeficiente angular PR:
Como os coeficientes angulares são iguais, os pontos estão alinhados.
Pratique mais com exercícios sobre condição de alinhamento de três pontos.
Veja também:
- Equação da reta: geral, reduzida e segmentária
- Exercícios sobre Geometria Analítica
- Exercícios sobre a distância entre ponto e reta
- Distância entre dois pontos: como calcular e exemplos
- Cálculo do Coeficiente Angular: fórmula e exercícios
Referências Bibliográficas
IEZZI, Gelson et al. Matemática: Ciência e Aplicações - Volume 3. 9ª ed. São Paulo: Saraiva, 2020.
DANTE, Luiz Roberto. Matemática: Contexto e Aplicações. 3ª ed. São Paulo: Ática, 2016.
ASTH, Rafael. Condição de alinhamento de três pontos: aprenda a verificar (com exemplos). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/condicao-de-alinhamento-de-tres-pontos/. Acesso em:


