Exercícios sobre geradores elétricos (com gabarito explicado)
Você está preparado para resolver as questões de geradores elétricos do ENEM?
Resolva as questões abaixo e teste seus conhecimentos.
Questão 1
Os geradores elétricos são dispositivos fundamentais para a produção de energia elétrica, transformando energia mecânica em energia elétrica através do fenômeno da indução eletromagnética. No Brasil, aproximadamente 65% da matriz energética provém de usinas hidrelétricas, onde a energia potencial da água é convertida em energia elétrica através desses geradores.
Em uma usina hidrelétrica experimental, um engenheiro realizou testes com um gerador elétrico variando alguns parâmetros como velocidade de rotação, número de espiras e intensidade do campo magnético. Os dados coletados estão apresentados no gráfico abaixo, que mostra a tensão elétrica gerada (em volts) em função da velocidade angular (em rad/s) para três configurações diferentes do gerador.
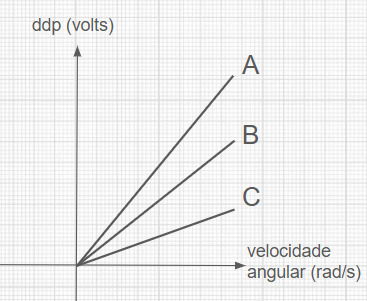
Com base nas informações apresentadas e nos conhecimentos sobre geradores elétricos, analise as afirmações a seguir:
I. A força eletromotriz induzida em um gerador é diretamente proporcional à taxa de variação do fluxo magnético.
II. A configuração A provavelmente possui o maior número de espiras ou o campo magnético mais intenso entre as três configurações apresentadas.
III. Se dobrarmos simultaneamente o número de espiras e reduzirmos à metade a intensidade do campo magnético, a tensão gerada permanecerá inalterada.
IV. Para obter uma tensão de 60 V utilizando a configuração C, seria necessário aumentar a velocidade angular para além do limite mecânico seguro do gerador.
Está correto apenas o que se afirma em:
a) I e II
b) I, II e III
c) II e IV
d) I, III e IV
Resposta correta: alternativa b) I, II e III
Vamos analisar cada afirmação para resolver a questão:
Afirmação I: "A força eletromotriz induzida em um gerador é diretamente proporcional à taxa de variação do fluxo magnético."
Esta afirmação está correta de acordo com a Lei de Faraday-Lenz. A força eletromotriz (ε) induzida em um circuito é dada por:
Quanto maior a taxa de variação do fluxo magnético, maior será a força eletromotriz induzida.
Afirmação II: "A configuração A provavelmente possui o maior número de espiras ou o campo magnético mais intenso entre as três configurações apresentadas."
Esta afirmação também está correta. No gráfico, a reta A apresenta a maior inclinação, o que significa que para uma mesma velocidade angular, ela produz a maior tensão. Pela Lei de Faraday, a tensão induzida é proporcional ao número de espiras (N) e à intensidade do campo magnético (B). Como a reta A gera mais tensão para a mesma velocidade, ela deve ter maior número de espiras e/ou campo magnético mais intenso.
Afirmação III: "Se dobrarmos simultaneamente o número de espiras e reduzirmos à metade a intensidade do campo magnético, a tensão gerada permanecerá inalterada."
Esta afirmação está correta. A tensão induzida é proporcional tanto ao número de espiras (N) quanto à intensidade do campo magnético (B). Se dobrarmos N (multiplicando por 2) e reduzirmos B à metade (multiplicando por 0,5), o produto N×B permanecerá o mesmo, resultando na mesma tensão induzida para uma dada velocidade angular.
Afirmação IV: "Para obter uma tensão de 60 V utilizando a configuração C, seria necessário aumentar a velocidade angular para além do limite mecânico seguro do gerador."
Não temos informações suficientes para determinar se 60 V estaria além do limite mecânico seguro do gerador. O texto não especifica qual seria esse limite, nem fornece valores numéricos precisos no gráfico para calcularmos qual velocidade angular seria necessária para atingir 60 V na configuração C. Portanto, esta afirmação não pode ser considerada correta com base apenas nas informações fornecidas.
Questão 2
O acesso à energia elétrica é fundamental para o desenvolvimento socioeconômico e qualidade de vida. Em regiões remotas da Amazônia, onde a extensão da rede elétrica convencional é inviável, comunidades ribeirinhas têm adotado sistemas autônomos de geração de energia.
Em uma dessas comunidades, instalou-se um sistema híbrido composto por painéis solares fotovoltaicos e um gerador a diesel para garantir fornecimento contínuo de eletricidade. Durante o dia, os painéis solares fornecem energia com força eletromotriz de 24 V e resistência interna de 0,5 Ω. À noite, quando necessário, utiliza-se o gerador a diesel que possui força eletromotriz de 24 V e resistência interna de 2,0 Ω.
A comunidade utiliza diversos equipamentos elétricos como lâmpadas LED, refrigerador para conservação de vacinas, pequena bomba dʼágua e equipamentos de comunicação. O consumo total equivale a uma resistência de carga de 6,0 Ω.
Assinale a alternativa correta.
a) A potência elétrica fornecida pelo gerador a diesel para a comunidade é maior que a fornecida pelos painéis solares, considerando a mesma resistência de carga, devido à menor resistência interna do gerador a diesel.
b) A tensão nos terminais do painel solar quando conectado à carga é de 24 V, pois a força eletromotriz independe da resistência interna do gerador.
c) A corrente elétrica fornecida pelo painel solar ao circuito externo é de aproximadamente 3,7 A, enquanto a fornecida pelo gerador a diesel é de aproximadamente 3,0 A.
d) O rendimento do sistema de geração é maior durante a noite, quando o gerador a diesel está em funcionamento, pois combustíveis fósseis produzem maior densidade energética que a radiação solar.
Resposta correta: alternativa c) A corrente elétrica fornecida pelo painel solar ao circuito externo é de aproximadamente 3,7 A, enquanto a fornecida pelo gerador a diesel é de aproximadamente 3,0 A.
Vamos primeiro calcular a corrente em cada caso. Lembre que . Temos:
Agora, vamos determinar a potência fornecida por cada um dos geradores. Lembre que P = R . i².
A potência fornecida pelo painel solar é maior que a fornecida pelo gerador a diesel.
Vamos determinar agora, a tensão nos terminais. Lembre que U = ε - r·i
Por fim, vamos determinar os rendimentos () dos geradores. Lembre que:
η = Potência útil/Potência total = R·i²/(ε·i) = R·i/ε = R/(R+r). Assim:
O rendimento é maior durante o dia, com o painel solar.
Questão 3
Os sistemas de energia de emergência são fundamentais em hospitais, garantindo o funcionamento ininterrupto de equipamentos médicos essenciais durante quedas de energia. Em um hospital do interior brasileiro, foi instalado um sistema de backup composto por um gerador elétrico que aciona automaticamente quando ocorre falha no fornecimento da rede elétrica.
Durante um teste de manutenção preventiva, o técnico responsável montou um circuito simples para verificar o funcionamento do gerador, conforme representado na figura abaixo:
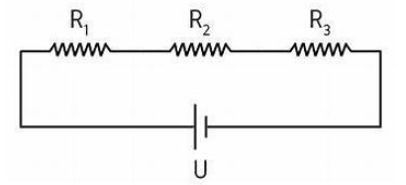
No teste, o gerador apresentou força eletromotriz (ε) de 120 V e resistência interna (r) de 2 Ω. O técnico mediu a corrente no circuito e a tensão nos terminais do gerador, anotando os valores para seu relatório.
Após finalizar os testes, verificou que o gerador estava operando dentro dos parâmetros esperados, garantindo assim a segurança energética do hospital em casos de emergência.
Analise o circuito de teste e assinale a alternativa correta.
a) A corrente elétrica que circula no circuito durante o teste é de 4 A, e a tensão nos terminais do gerador é de 112 V.
b) A potência total dissipada nos resistores externos (R₁, R₂ e R₃) é de 480 W, representando 90% da potência fornecida pelo gerador.
c) Se a resistência interna do gerador fosse nula (r = 0 Ω), a corrente no circuito seria de 4 A, igual à situação real de teste.
d) O rendimento do gerador nesse circuito de teste é de aproximadamente 94%, indicando que apenas 6% da energia é perdida na resistência interna.
Resposta correta: alternativa d) O rendimento do gerador nesse circuito de teste é de aproximadamente 94%, indicando que apenas 6% da energia é perdida na resistência interna.
Vamos resolver o problema passo a passo, analisando o circuito fornecido:
O enunciado trouxe os seguintes dados:
Força eletromotriz do gerador: ε = 120 V
Resistência interna do gerador: r = 2 Ω
Resistores externos: R₁ = 10 Ω, R₂ = 15 Ω, R₃ = 5 Ω
Passo 1: vamos calcular a resistência equivalente do circuito externo (Req)
Como os resistores estão em série, vem:
Req = R₁ + R₂ + R₃ = 10 + 15 + 5 = 30 Ω
Passo 2: cálculo da resistência total do circuito (RT):
RT = r + Req = 2 + 30 = 32 Ω
Passo 3: cálculo da corrente elétrica do circuito (i) na situação real do teste:
i = ε / RT = 120 / 32 = 3,75 A
Passo 4: cálculo da tensão nos terminais do gerador (U):
U = ε - r . i = 120 - 2 . 3,75 = 120 - 7,5 = 112,5 V
Passo 5: cálculo da potência dissipada nos resistores externos (Pext):
Pext = i² . Req = (3,75)² . 30 = 14,0625 . 30 = 421,875 W
Passo 6: cálculo da potência total fornecida pelo gerador (Ptotal):
Ptotal = ε . i = 120 . 3,75 = 450 W
Passo 7: cálculo do rendimento do gerador (η):
η = Pext / Ptotal = 421,875 / 450 = 0,9375 = 93,75%
Questão 4
Em comunidades rurais isoladas da região Norte do Brasil, os geradores elétricos são fundamentais para garantir o acesso à energia elétrica, permitindo a conservação de alimentos, o uso de equipamentos de saúde e comunicação. Em uma dessas comunidades, está sendo implementado um projeto de microgeração distribuída utilizando um pequeno gerador hidrelétrico instalado em um córrego local.
O engenheiro responsável pelo projeto realizou testes para determinar as características elétricas do gerador antes de sua instalação definitiva. Para isso, montou um circuito de teste conforme a figura abaixo:
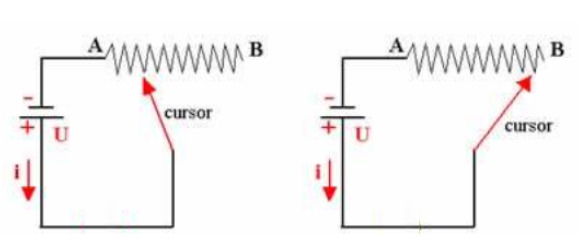
Durante os testes, foram coletados dados da corrente elétrica (i) e da tensão nos terminais do gerador (U) para diferentes valores de resistência externa (R). Os resultados estão apresentados na tabela:
Resistência, R (Ω) |
Corrente, i (A) | Tensão, U (V) |
|---|---|---|
| 1,0 | 6,0 | 6,0 |
| 2,0 | 4,0 | 8,0 |
| 3,0 | 3,0 | 9,0 |
| 4,0 | 2,4 | 9,6 |
| 5,0 | 2,0 | 10,0 |
Assinale a alternativa correta.
a) A força eletromotriz do gerador é 12 V, e quando o circuito está em curto-circuito (R = 0), a corrente elétrica será infinita, caracterizando uma situação de perigo.
b) A potência elétrica máxima fornecida pelo gerador ao circuito externo ocorre quando a resistência externa é igual a 2 Ω, com valor de 32 W.
c) A resistência interna do gerador é 1 Ω, e quando o reostato é ajustado para este mesmo valor, o rendimento do gerador é de 50%.
d) A força eletromotriz do gerador é 12 V, e sua resistência interna é 1 Ω, o que limita a corrente máxima do circuito a 12 A.
Resposta correta: alternativa c) A resistência interna do gerador é 1 Ω, e quando o reostato é ajustado para este mesmo valor, o rendimento do gerador é de 50%.
Vamos resolver o problema utilizando os dados da tabela e as equações relacionadas de geradores elétricos.
Passo 1: cálculo da força eletromotriz (ε) e da resistência interna (r) do gerador.
Para um gerador elétrico, a relação entre tensão nos terminais (U), força eletromotriz (ε), corrente (i) e resistência interna (r) é dada por:
U = ε - r . i
Podemos usar dois pontos da tabela para formar um sistema de equações:
Para R = 1,0 Ω, temos: 6,0 = ε - r . 6,0
Para R = 5,0 Ω, temos: 10,0 = ε - r . 2,0
Vamos resolver esse sistema subtraindo a primeira equação da segunda. Ficamos com:
10,0 - 6,0 = (ε - r . 2,0) - (ε - r . 6,0)
4,0 = r . 6,0 - r . 2,0
4,0 = r . 4,0
r = 1,0 Ω
Substituindo agora r = 1,0 Ω na primeira equação:
6,0 = ε - 1,0·6,0
6,0 = ε - 6,0
ε = 12,0 V
Alternativamente, podemos verificar usando a Lei de Ohm que diz que:
i = ε/(R + r)
Para cada ponto da tabela, isso deve ser verdadeiro. Por exemplo:
Para R = 1,0 Ω, temos: 6,0 = ε/(1,0 + 1,0) → ε = 12,0 V
Para R = 2,0 Ω, temos: 4,0 = ε/(2,0 + 1,0) → ε = 12,0 V
Assim, confirmamos que ε = 12,0 V e r = 1,0 Ω.
Passo 2: vamos verificar o que acontece em curto-circuito, ou seja, quando R = 0.
Para R = 0, a corrente seria igual a: i = ε / (R + r) = 12,0 / (0 + 1,0) = 12,0 A
A corrente não seria infinita no curto-circuito, seria igual a 12,0 A.
Passo 3: cálculo da potência fornecida ao circuito externo para cada valor de R.
A potência fornecida ao circuito externo (resistência R) é dada por: P = i² . R
Calculando para cada valor da tabela, temos:
Para R = 1,0 Ω vem: P = (6,0)²·1,0 = 36,0 W
Para R = 2,0 Ω vem: P = (4,0)²·2,0 = 32,0 W
Para R = 3,0 Ω vem: P = (3,0)²·3,0 = 27,0 W
Para R = 4,0 Ω vem: P = (2,4)²·4,0 = 23,04 W
Para R = 5,0 Ω vem: P = (2,0)²·5,0 = 20,0 W
A potência máxima ocorre quando R = 1,0 Ω, e tem valor de 36,0 W.
Passo 4: cálculo do rendimento para R = r = 1,0 Ω.
Lembre que o rendimento é dado por:
η = Pútil / Ptotal = PR / (PR + Pr) = R . i² / (R . i² + r . i²) = R / (R + r)
Quando R = r = 1,0 Ω, ficamos com:
η = 1,0 / (1,0 + 1,0) = 0,5 = 50%
Passo 5: vamos analisar o comportamento da potência dissipada na resistência interna.
A potência dissipada na resistência interna é: Pr = i² . r
À medida que R aumenta, vemos pela tabela que a corrente i diminui. Como Pr depende do quadrado da corrente, ela também irá diminuir com o aumento de R. No limite, quando R→∞ (ou seja, no caso do circuito aberto) temos: i→0, e Pr→0.
Observação: a alternativa d) traz que a força eletromotriz do gerador é 12 V, e sua resistência interna é 1 Ω, o que limita a corrente máxima do circuito a 12 A, estando aparentemente correta. Mas, o enunciado "limita a corrente máxima do circuito a 12 A" pode ser interpretado como se houvesse um limitador externo, quando na verdade, é simplesmente o resultado das leis de circuito.
Questão 5
Na cidade de Belo Horizonte, uma escola técnica implementou um projeto sustentável utilizando um sistema de geração híbrida de energia elétrica, combinando painéis fotovoltaicos e pequenos geradores eólicos. O projeto visa não apenas reduzir a conta de energia da instituição, mas também servir como laboratório prático para os estudantes dos cursos técnicos em Eletrotécnica e Meio Ambiente.
O professor explicou que, diferentemente de uma pilha ou bateria convencional, a força eletromotriz do gerador eólico varia de acordo com a velocidade do vento. No dia do experimento, com velocidade do vento constante, o gerador apresentou uma força eletromotriz de 24 V e resistência interna de 2 Ω.
Os alunos realizaram medições com diferentes resistências de carga e anotaram os resultados no gráfico abaixo, que mostra a relação entre a potência elétrica útil em função da resistência da carga utilizada.
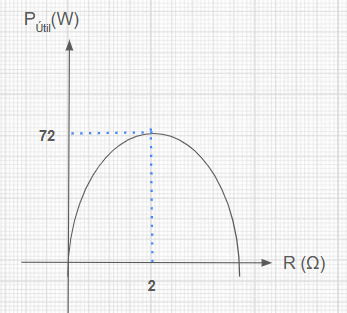
Assinale a alternativa correta.
a) Caso o circuito permanecesse aberto (sem carga conectada), a tensão nos terminais do gerador seria nula, pois não haveria corrente elétrica circulando.
b) A potência máxima fornecida à carga ocorre quando a resistência da carga é igual à resistência interna do gerador, o que comprova o teorema da máxima transferência de potência.
c) O rendimento do gerador é máximo quando a carga conectada possui resistência de 2 Ω, atingindo 50% nessa condição.
d) Se a velocidade do vento aumentar, elevando a força eletromotriz para 36 V, a potência máxima transferida à carga seria triplicada, mantendo-se a resistência interna constante.
Resposta correta: alternativa b) A potência máxima fornecida à carga ocorre quando a resistência da carga é igual à resistência interna do gerador, o que comprova o teorema da máxima transferência de potência.
Vamos resolver a questão passo a passo.
Foram dadas as seguintes informações no enunciado:
Força eletromotriz do gerador (ε): 24 V
Resistência interna do gerador (r): 2 Ω
Potência máxima fornecida à carga: 72 W para R = 2 Ω
Passo 1: vamos determinar a corrente e a tensão com carga de 6 Ω.
A corrente no circuito quando conectada uma carga R é dada por:
i = ε / (r + R), que nesse caso fica: i = 24 / (2 + 6) = 24 / 8 = 3 A
A tensão nos terminais do gerador é: U = ε - r . i = 24 - 2 . 3 = 24 - 6 = 18 V
Portanto, com uma carga de 6 Ω, a corrente é de 3 A e a tensão nos terminais é igual a 18 V.
Passo 2: vamos analisar a condição de máxima transferência de potência.
O teorema da máxima transferência de potência estabelece que a potência máxima é transferida de um gerador para uma carga quando a resistência da carga é igual à resistência interna do gerador.
De acordo com o gráfico, a potência máxima ocorre quando R = 2 Ω, que é igual à resistência interna do gerador. Isso confirma o teorema da máxima transferência de potência.
Passo 3: cálculo do rendimento com R = 2 Ω.
O rendimento de um gerador é dado por:
η = Pútil / Ptotal = PR / (PR + Pr) = R . i² / (R . i² + r . i²) = R / (R + r)
Quando R = r = 2 Ω, temos:
η = 2 / (2 + 2) = 2 / 4 = 0,5 = 50%
Passo 4: vamos analisar o efeito do aumento da força eletromotriz.
A potência máxima transferida à carga é dada por:
Pmáx = ε² / 4r quando R = r
Se ε aumentar de 24 V para 36 V, teremos:
Potência máxima inicial: P₁ = (24)² / (4 . 2) = 576 / 8 = 72 W
Nova potência máxima: P₂ = (36)² / (4 . 2) = 1296 / 8 = 162 W
A razão entre as potências é:
P₂ / P₁ = 162 / 72 = 2,25
Portanto, a potência máxima seria multiplicada por 2,25 (aumentaria 125%), não seria triplicada.
Passo 5: vamos analisar o que ocorre quando o circuito está aberto.
Em um circuito aberto R → ∞ e a corrente é nula ou i = 0. A tensão nos terminais do gerador é: U = ε - r . i = ε - r . 0 = 24 V
Portanto, com o circuito aberto, a tensão nos terminais do gerador é igual à força eletromotriz, não seria nula.
Questão 6
O Brasil, por sua extensa rede hidrográfica, tem na energia hidrelétrica sua principal fonte de geração de eletricidade. Na usina hidrelétrica de Itaipu, localizada na fronteira entre Brasil e Paraguai, a energia potencial da água é convertida em energia elétrica por meio de geradores acoplados à turbinas. A usina conta com 20 unidades geradoras, com capacidade total de 14.000 MW, suficiente para abastecer aproximadamente 10% da demanda energética brasileira.
Em aulas práticas de Física em uma escola técnica, os alunos estudam o funcionamento de geradores elétricos utilizando modelos em escala reduzida. Em um experimento específico, um professor montou um circuito para demonstrar as relações entre as principais grandezas associadas a um gerador elétrico. O circuito continha um gerador (com força eletromotriz ε e resistência interna r), um amperímetro em série, um voltímetro em paralelo com o gerador, e um conjunto de resistores que podiam ser associados de diferentes formas.
Durante o experimento, os alunos mediram a corrente elétrica (i) e a tensão nos terminais do gerador (U) para diferentes configurações de resistência equivalente (R) no circuito externo. Com os dados obtidos, eles construíram o gráfico mostrado abaixo:
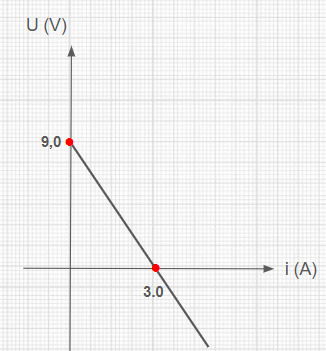
Analise as afirmações a seguir e marque a alternativa correta.
I. A força eletromotriz do gerador utilizado no experimento é 9,0 V.
II. A resistência interna do gerador pode ser determinada pela razão entre a força eletromotriz e a corrente de curto-circuito, resultando em 3,0 Ω.
III. Se uma resistência externa de 6,0 Ω for conectada ao gerador, a corrente no circuito será de 1,0 A.
IV. O rendimento máximo desse gerador é obtido quando a resistência externa é muito maior que a resistência interna, aproximando-se de 100%.
V. A potência elétrica dissipada na resistência interna do gerador é maior quando o circuito está em curto-circuito.
Estão corretas as afirmações:
a) I, II e III apenas.
b) I, III e IV apenas.
c) II, IV e V apenas.
d) I, II, III, IV e V.
Resposta correta: alternativa d) I, II, III, IV e V.
Vamos analisar cada uma das afirmações com base nas informações fornecidas e nos conceitos de geradores.
Dados obtidos do gráfico:
Para i = 0 A temos U = 9,0 V e circuito aberto
Quando U = 0 V temos i = 3,0 A e curto-circuito
Afirmação I: A força eletromotriz do gerador utilizado no experimento é 9,0 V.
Para um gerador elétrico, a relação entre a tensão nos terminais (U), a força eletromotriz (ε), a corrente (i) e a resistência interna (r) é dada por:
U = ε - r . i
Quando o circuito está aberto (i = 0 A), a tensão nos terminais é igual à força eletromotriz:
U = ε - r . 0 = ε
Pelo gráfico temos que: quando i = 0 A, U = 9,0 V, e portanto, ε = 9,0 V.
A affirmação I está correta.
Afirmação II: A resistência interna do gerador pode ser determinada pela razão entre a força eletromotriz e a corrente de curto-circuito, resultando em 3,0 Ω.
Quando ocorre curto-circuito, temos U = 0 V e:
0 = ε - r . icurto
r . icurto = ε
r = ε / icurto
Substituindo os valores, ficamos com: r = 9,0 / 3,0 = 3,0 Ω
A afirmação II está correta.
Afirmação III: Se uma resistência externa de 6,0 Ω for conectada ao gerador, a corrente no circuito será de 1,0 A.
A corrente em um circuito com resistência externa R é dada por:
i = ε / (r + R) = 9,0 / (3,0 + 6,0) = 9,0 / 9,0 = 1,0 A
Podemos verificar se este valor é consistente com o gráfico:
Para i = 1,0 A, a tensão nos terminais é:
U = ε - r . i = 9,0 - 3,0 . 1,0 = 9,0 - 3,0 = 6,0 V
O ponto (1,0 A, 6,0 V) deve estar na reta do gráfico, o que é consistente com uma reta que vai de (0A, 9,0V) a (3,0A, 0 V).
A afirmação III está correta.
Afirmação IV: O rendimento máximo desse gerador é obtido quando a resistência externa é muito maior que a resistência interna, aproximando-se de 100%.
O rendimento de um gerador é dado por:
η = Pútil / Ptotal = R . i² / (ε . i) = R . i / ε = R / (R + r)
Quando R >> r, o rendimento se aproxima de:
η ≈ R / R = 1 ou 100%
A afirmação IV está correta.
Afirmação V: A potência elétrica dissipada na resistência interna do gerador é maior quando o circuito está em curto-circuito.
A potência dissipada na resistência interna é: Pr = r . i²
A corrente é máxima no curto-circuito quando i = 3,0 A. Portanto, a potência dissipada na resistência interna também atinge seu valor máximo nessa condição:
Para qualquer outra condição, a corrente será menor, e como Pr depende do quadrado da corrente, a potência dissipada será menor.
A afirmação V está correta.
Veja também geradores elétricos: o que são, tipos e exemplos e continue praticando com
exercícios sobre associação de geradores elétricos (com gabarito explicado)
exercícios sobre corrente elétrica (com gabarito explicado)
exercícios sobre amperímetro e voltímetro (com gabarito explicado).
SOUTO, Ana. Exercícios sobre geradores elétricos (com gabarito explicado). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-sobre-geradores-eletricos-com-gabarito-explicado/. Acesso em:


