Progressão Aritmética (P.A.)

Rafael C. Asth

Professor de Matemática e Física

A Progressão Aritmética (P.A.) é uma sequência de números onde a diferença entre dois termos consecutivos é sempre a mesma. Essa diferença constante é chamada de razão da P.A..

Sendo assim, a partir do segundo elemento da sequência, os números que surgem são resultantes da soma da constante com o valor do elemento anterior.

Isso é o que a diferencia da progressão geométrica (P.G.), pois nesta, os números são multiplicados pela razão, enquanto na progressão aritmética, eles são somados.

As progressões aritméticas podem apresentar um número determinado de termos (P.A. finita) ou um número infinito de termos (P.A. infinita).

Para indicar que uma sequência continua indefinidamente utilizamos reticências, por exemplo:

• a sequência (4, 7, 10, 13, 16, ...) é uma P.A. infinita.
• a sequência (70, 60, 50, 40, 30, 20, 10) é uma P.A. finita.

Cada termo de uma P.A. é identificado pela posição que ocupa na sequência e para representar cada termo utilizamos uma letra (normalmente a letra a) seguida de um número que indica sua posição na sequência.

Por exemplo, o termo a₄ na P.A (2, 4, 6, 8, 10) é o número 8, pois é o número que ocupa a 4ª posição na sequência.

Classificação de uma P.A.

De acordo com o valor da razão, as progressões aritméticas são classificadas em:

• Constante: quando a razão for igual a zero. Por exemplo: (4, 4, 4, 4, 4...), sendo r = 0.
• Crescente: quando a razão for maior que zero. Por exemplo: (2, 4, 6, 8,10...), sendo r = 2.
• Decrescente: quando a razão for menor que zero (15, 10, 5, 0, - 5,...), sendo r = - 5

Propriedades da P.A.

1ª propriedade:

Em uma P.A. finita, a soma de dois termos equidistantes dos extremos é igual à soma dos extremos.

Exemplo

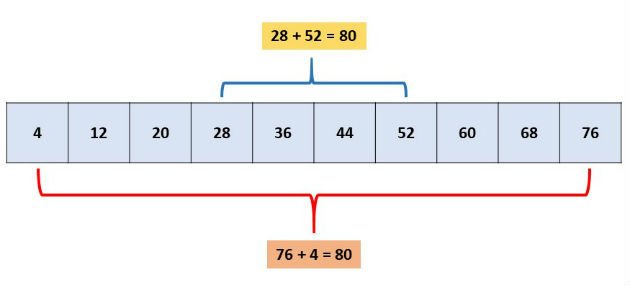
2ª propriedade:

Considerando três termos consecutivos de uma P.A., o termo do meio será igual a média aritmética dos outros dois termos.

Exemplo

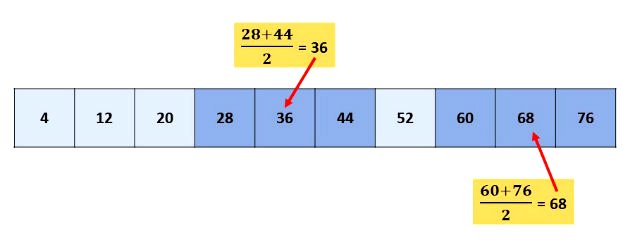
3ª propriedade:

Em uma P.A. finita com número de termos ímpar, o termo central será igual a média aritmética entre termos equidistantes deste. Esta propriedade deriva da primeira.

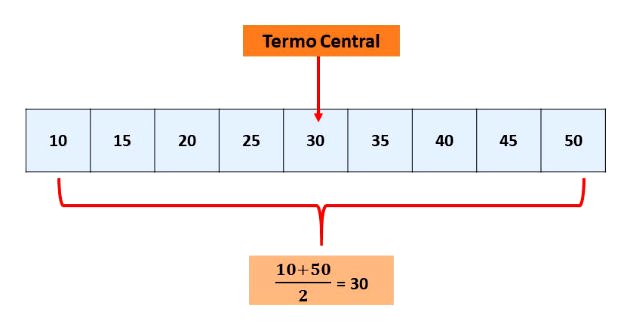
Fórmula do Termo Geral

Onde,

an: termo que queremos calcular
a1: primeiro termo da P.A.
n: posição do termo que queremos descobrir
r: razão

Explicação da fórmula

Como a razão de uma P.A. é constante, podemos calcular seu valor a partir de quaisquer termos consecutivos, ou seja:

Sendo assim, podemos encontrar o valor do segundo termo da P.A. fazendo:

Para encontrar o terceiro termo utilizaremos o mesmo cálculo:

Substituindo o valor de a₂, que encontramos anteriormente, temos:

Se seguirmos o mesmo raciocínio, podemos encontrar:

Observando os resultados encontrados, notamos que cada termo será igual a soma do primeiro termo com a razão multiplicada pela posição anterior.

Esse cálculo é expresso através da fórmula do termo geral da P.A., que nos permite conhecer qualquer elemento de uma progressão aritmética.

Exemplo

Calcule o 10° termo da P.A.: (26, 31, 36, 41, ...)

Solução

Primeiro, devemos identificar que:

a₁ = 26
r = 31 - 26 = 5
n = 10 (10º termo).

Substituindo esses valores na fórmula do termo geral, temos:

a_n = a₁ + (n - 1) . r
a₁₀ = 26 + (10-1) . 5
a₁₀ = 26 + 9 .5
a₁₀ = 71

Portanto, o décimo termo da progressão aritmética indicada é igual a 71.

Fórmula do termo geral a partir de um termo k qualquer

Muitas vezes, para definir um termo genérico qualquer, que chamamos de an, não temos o primeiro termo a1, mas conhecemos outro qualquer, que chamamos de ak.

Podemos usar a fórmula do termo geral a partir de um termo k qualquer:

Repare que a única diferença, foi a mudança do índice 1 na primeira fórmula, pelo k, na segunda.

Sendo,

an: o n-ésimo termo da P.A. (um termo numa posição n qualquer)
ak: o k-ésimo termo de uma P.A. (um termo numa posição k qualquer)
r: a razão

Soma dos Termos de uma P.A.

Para encontrar a soma dos termos de uma P.A. finita, basta utilizar a fórmula:

Onde,

S_n: soma dos n primeiros termos da P.A.
a₁: primeiro termo da P.A.
a_n: ocupa a enésima posição na sequência (uma termo na posição n)
n: posição do termo

Leia também sobre PA e PG.

Exercício Resolvido

Exercício 1

PUC/RJ - 2018

Sabendo que os números da sequência (y, 7, z, 15) estão em progressão aritmética, quanto vale a soma y + z?

a) 20
b) 14
c) 7
d) 3,5
e) 2

Exercício 2

IFRS - 2017

Na figura abaixo, temos uma sequência de retângulos, todos de altura a. A base do primeiro retângulo é b e dos retângulos subsequentes é o valor da base do anterior mais uma unidade de medida. Sendo assim, a base do segundo retângulo é b+1 e do terceiro b+2 e assim sucessivamente.

Considere as afirmativas abaixo.

I - A sequência das áreas dos retângulos é uma progressão aritmética de razão 1.
II - A sequência das áreas dos retângulos é uma progressão aritmética de razão a.
III - A sequência das áreas dos retângulos é uma progressão geométrica de razão a.
IV - A área do enésimo retângulo (A_n) pode ser obtida pela fórmula A_n = a . (b + n - 1).

Assinale a alternativa que contém a(as) afirmativa(s) correta(s).

a) I.
b) II.
c) III.
d) II e IV.
e) III e IV.

Exercício 3

UERJ

Admita a realização de um campeonato de futebol no qual as advertências recebidas pelos atletas são representadas apenas por cartões amarelos. Esses cartões são convertidos em multas, de acordo com os seguintes critérios:

• Os dois primeiros cartões recebidos não geram multas;
• O terceiro cartão gera multa de R$500,00.
• Os cartões seguintes geram multas cujos valores são sempre acrescidos de R$500,00 em relação ao valor da multa anterior.

No quadro, indicam-se as multas relacionadas aos cinco primeiros cartões aplicados a um atleta.

Considere um atleta que tenha recebido 13 cartões amarelos durante o campeonato. O valor total, em reais, das multas geradas por todos esses cartões equivale a:

a)30 000
b)33 000
c)36 000
d)39 000

Resolva mais exercícios em:

Progressão Aritmética - Exercícios

Saiba mais, lendo também:

• Sequência Numérica
• Progressão Geométrica
• Progressão Geométrica - Exercícios
• Exercícios sobre PA e PG
• Fórmulas de Matemática
• Sequência de Fibonacci

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.