Média Aritmética
A Média Aritmética de um conjunto de dados é obtida somando todos os valores e dividindo o valor encontrado pelo número de dados desse conjunto.
É muito utilizada em estatística como uma medida de tendência central.
Pode ser simples, onde todos os valores possuem a mesma importância, ou ponderada, quando considera pesos diferentes aos dados.
Média Aritmética Simples
Esse tipo de média funciona de forma mais adequada quando os valores são relativamente uniformes.
Por ser sensível aos dados, nem sempre fornece os resultados mais adequados.
Isso porque todos os dados possuem a mesma importância (peso).
Fórmula
![]()
Onde,
Ms: média aritmética simples
x1, x2, x3,...,xn: valores dos dados
n: número de dados
Exemplo:
Sabendo que as notas de um aluno foram: 8,2; 7,8; 10,0; 9,5; 6,7, qual a média que ele obteve no curso?
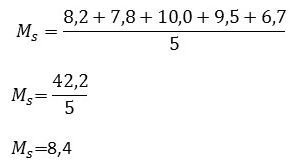
Média Aritmética Ponderada
A média aritmética ponderada é calculada multiplicando cada valor do conjunto de dados pelo seu peso.
Depois, encontra-se a soma desses valores que será dividida pela soma dos pesos.
Fórmula
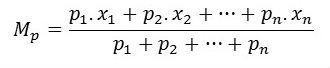
Onde,
Mp: Média aritmética ponderada
p1, p2,..., pn: pesos
x1, x2,...,xn: valores dos dados
Exemplo:
Considerando as notas e os respectivos pesos de cada uma delas, indique qual a média que o aluno obteve no curso.
| Disciplina | Nota | Peso |
|---|---|---|
| Biologia | 8,2 | 3 |
| Filosofia | 10,0 | 2 |
| Física | 9,5 | 4 |
| Geografia | 7,8 | 2 |
| História | 10,0 | 2 |
| Língua Portuguesa | 9,5 | 3 |
| Matemática | 6,7 | 4 |
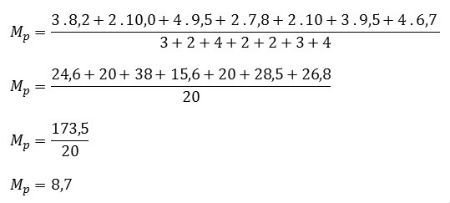
Leia:
- Média Aritmética Ponderada
- Média Geométrica
- Média, Moda e Mediana
- Variância e Desvio Padrão
- Frequência Relativa
Exercícios do Enem Comentados
1. (ENEM-2012) A tabela a seguir mostra a evolução da receita bruta anual nos três últimos anos de cinco microempresas (ME) que se encontram à venda.
| ME |
2009 (em milhares de reais) |
2010 (em milhares de reais) |
2011 (em milhares de reais) |
|---|---|---|---|
| Alfinetes V | 200 | 220 | 240 |
| Balas W | 200 | 230 | 200 |
| Chocolates X | 250 | 210 | 215 |
| Pizzaria Y | 230 | 230 | 230 |
| Tecelagem Z | 160 | 210 | 245 |
Um investidor deseja comprar duas das empresas listadas na tabela. Para tal, ele calcula a média da receita bruta anual dos últimos três anos (de 2009 até 2011) e escolhe as duas empresas de maior média anual.
As empresas que este investidor escolhe comprar são:
a) Balas W e Pizzaria Y.
b) Chocolates X e Tecelagem Z.
c) Pizzaria Y e Alfinetes V.
d) Pizzaria Y e Chocolates X.
e) Tecelagem Z e Alfinetes V.
2. (ENEM-2014) Ao final de uma competição de ciências em uma escola, restaram apenas três candidatos.
De acordo com as regras, o vencedor será o candidato que obtiver a maior média ponderada entre as notas das provas finais de química e física, considerando, respectivamente, os pesos 4 e 6 para elas. As notas são sempre números inteiros.
Por questões médicas, o candidato II ainda não fez a prova final de química. No dia em que sua avaliação for aplicada, as notas dos outros dois candidatos, em ambas as disciplinas, já terão sido divulgadas.
O quadro apresenta as notas obtidas pelos finalistas nas provas finais.
| Candidato | Química | Física |
|---|---|---|
| I | 20 | 23 |
| II | x | 25 |
| III | 21 | 18 |
A menor nota que o candidato II deverá obter na prova final de química para vencer a competição é:
a) 18
b) 19
c) 22
d) 25
e) 26
Veja também:
- Exercícios de Média Aritmética
- Exercícios de Média, Moda e Mediana
- Exercícios sobre frequência absoluta e relativa
- Estatística
- Estatística - Exercícios
- Desvio Padrão
- Medidas de Dispersão
- Frequência Absoluta
GOUVEIA, Rosimar. Média Aritmética. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/media/. Acesso em:



