Exercícios de Média Aritmética (com respostas explicadas)

Rafael C. Asth

Professor de Matemática e Física

Estude média aritmética com a lista de exercícios que o Toda Matéria preparou para você. Tire suas dúvidas com os exercícios resolvidos passo a passo.

Questão 1

Fernando está avaliando o preço médio de sua tarifa de energia elétrica nos cinco primeiros meses do ano. A planilha mostra os valores por mês, de janeiro a maio.

janeiro	fevereiro	março	abril	maio
R$ 173,00	R$ 113,58	R$ 145,67	R$ 98,50	R$ 123,60

Sua meta é fechar o semestre com um preço médio de R$ 130,00. Para alcançar a meta, o maior preço possível a pagar na tarifa do mês de junho, será de

a) R$ 109,05
b) R$ 125,65
c) R$ 130,87
d) R$ 98,55

Ver Resposta

Resposta correta: b) R$ 125,65

Para determinar o maior preço a ser pago para manter o preço médio na meta, devemos calcular a média aritmética nos seis meses. Chamando de X o preço a ser pago em junho, temos:

$numerador 173 vírgula 00 espaço mais espaço 113 vírgula 58 espaço mais espaço 145 vírgula 67 espaço mais espaço 98 vírgula 50 espaço mais espaço 123 vírgula 60 espaço mais espaço reto X sobre denominador 6 fim da fração igual a 130 numerador 654 vírgula 35 espaço mais espaço X sobre denominador 6 fim da fração igual a 130 654 vírgula 35 espaço mais espaço X espaço igual a espaço 130 espaço. espaço 6 654 vírgula 35 espaço mais espaço X espaço igual a espaço 780 654 vírgula 35 espaço mais espaço X espaço igual a espaço 780 X igual a 780 espaço menos espaço 654 vírgula 35 X igual a 125 vírgula 65$

Portanto, o preço máximo a se pagar na conta de junho, é de R$ 125,65.

Questão 2

Em uma escola de Ensino Fundamental um concurso estabelece regras para conceder uma bolsa de estudos para o Ensino Médio. Em cada bimestre os alunos do 9.º ano realizam uma avaliação e, após os quatro bimestres, as notas são somadas. Os quatro alunos finalistas são os que alcançam as maiores pontuações. Ganhará a bolsa aquele que possuir a média mais alta das quatro notas das avaliações.

As notas dos quatro alunos finalistas são:

	1º bimestre	2º bimestre	3º bimestre	4º bimestre
Aluno A	75	86	83	91
Aluno B	78	98	67	99
Aluno C	83	84	89	87
Aluno D	98	65	87	77

O aluno que ganhou a bolsa de estudos foi
a) o aluno A.
b) o aluno B.
c) o aluno C.
d) o aluno D.

Ver Resposta

Resposta correta: c) o aluno C.

Precisamos calcular a média aritmética dos quatro alunos.

Aluno A

$numerador 75 espaço mais espaço 86 espaço mais espaço 83 espaço mais espaço 91 sobre denominador 4 fim da fração igual a 83 vírgula 75$

Aluno B

$numerador 78 espaço mais espaço 98 espaço mais espaço 67 espaço mais espaço 99 sobre denominador 4 fim da fração igual a 85 vírgula 50$

Aluno C

$numerador 83 espaço mais espaço 84 espaço mais espaço 89 espaço mais espaço 87 espaço sobre denominador 4 fim da fração igual a 85 vírgula 75$

Aluno D

$numerador 98 espaço mais espaço 65 espaço mais espaço 87 espaço mais espaço 77 espaço sobre denominador 4 fim da fração igual a 81 vírgula 75 espaço$

Portanto, o aluno C ganhou a bolsa de estudos.

Questão 3

Em duas turmas do 7.º ano do Ensino Fundamental, a média da turma A, que possui 23 alunos, foi 7,3. Ao total, a escola possui 52 alunos matriculados nos 7.ºˢ anos. A média geral dos alunos destas turmas foi de 7,5. Qual das duas turmas teve a maior média?

Ver Resposta

Resposta: a turma B.

Média da turma A

Chamando de X a soma das notas dos alunos da turma A:

$X sobre 23 igual a 7 vírgula 3 X espaço igual a espaço 23 espaço. espaço 7 vírgula 3 espaço igual a espaço 167 vírgula 9$

Média das duas turmas

A média é a soma das notas da turma A, que chamamos de X, com a soma das notas da turma B, que chamaremos de Y, dividido pelo total de alunos nas duas turmas, que é 52.

$numerador X espaço mais espaço Y sobre denominador 52 fim da fração igual a 7 vírgula 5$

Sabemos que X = 167,9, substituindo temos:

$numerador 167 vírgula 9 espaço mais espaço Y sobre denominador 52 fim da fração espaço igual a espaço 7 vírgula 5 espaço 167 vírgula 9 espaço mais espaço Y espaço igual a espaço 7 vírgula 5 espaço. espaço 52 167 vírgula 9 espaço mais espaço Y espaço igual a espaço 390 Y espaço igual a espaço 390 espaço menos espaço 167 vírgula 9 Y espaço igual a espaço 222 vírgula 1$

Números de alunos na turma B.

52 - 23 = 29

Média da turma B

A média será o total de notas dividido pelo total de alunos da turma.

$numerador 222 vírgula 1 sobre denominador 29 fim da fração aproximadamente igual 7 vírgula 66$

Sendo assim, a média da turma B é, aproximadamente, 7,66.

Portanto, a turma B teve a maior média.

Questão 4

A previsão do tempo para os próximos três dias é:

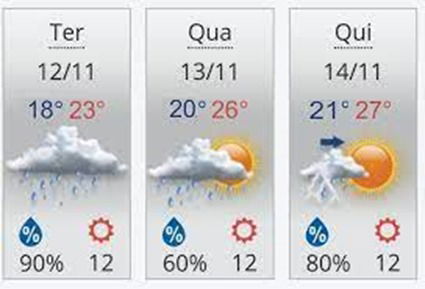
As médias das temperaturas mínima e máxima, para cada um dos próximos três dias, respectivamente, são:

a) 23,0 — 20,5 — 24,0
b) 20,5 — 23,0 — 26,0
c) 20,5 — 23,0 — 24,0
d) 20,5 — 24,5 — 24,0
e) 25,5 — 23,0 — 24,0

Ver Resposta

Resposta correta: c) 20,5 - 23,0 - 24,0

Calculando a média das temperaturas máxima e mínima para cada dia, temos:

Terça 12/11

$numerador 18 espaço mais espaço 23 sobre denominador 2 fim da fração igual a 20 vírgula 5$

Quarta 13/11

$numerador 20 mais 26 sobre denominador 2 fim da fração igual a 23$

Quinta 14/11

$numerador 21 espaço mais espaço 27 sobre denominador 2 fim da fração igual a 24$

Questão 5

Gabriela está preocupada com suas notas em Matemática. Os critérios para aprovação na disciplina são:

A média das notas das três avaliações deve ser maior ou igual a 7. Caso o aluno não consiga atingir a média mínima, ele deve realizar uma avaliação de recuperação. Para ser aprovada, a média entre seu resultado nas três avaliações e a nota da recuperação, devem ter média igual ou maior a 6.

As notas de Gabriela foram:
Prova 1: 8
Prova 2: 5,2
Prova 3: 6,6

Caso Gabriela tenha ficado de recuperação, qual nota mínima ela deverá tirar na recuperação para ser aprovada?

Ver Resposta

Resposta: Na recuperação, Gabriela precisa tirar pelo menos 5,4.

Primeiro verificamos se Gabriela está de recuperação calculando a média entre as notas.

$numerador 8 espaço mais espaço 5 vírgula 2 espaço mais espaço 6 vírgula 6 sobre denominador 3 fim da fração igual a 6 vírgula 6$

Como a média está abaixo de 7, ela ficou de recuperação. Para saber que nota mínima ela precisa na recuperação, calculamos uma nova média.

Chamando de X o valor da nota que ela deverá tirar para ter média pelo menos igual a 6, temos:

$numerador 6 vírgula 6 espaço mais espaço X sobre denominador 2 fim da fração igual a 6 6 vírgula 6 espaço mais espaço X espaço igual a espaço 6 espaço. espaço 2 6 vírgula 6 espaço mais espaço X espaço igual a espaço 12 X espaço igual a espaço 12 espaço menos espaço 6 vírgula 6 X espaço igual a espaço 5 vírgula 4$

Desta forma, Gabriela precisa de, pelo menos, 5,4 na nota da avaliação de recuperação.

Pratique também com Exercícios de Média, Moda e Mediana.

Questão 6

Pedro e Natália estão disputando quem consegue a melhor média aritmética no jogo de lançamento de dados. Eles lançam dois dados e somam os pontos. Após três lançamentos eles calculam a média e, aquele que obtiver a maior média dos lançamentos vencerá o jogo.

Natália obteve os seguintes pontos nos lançamentos:

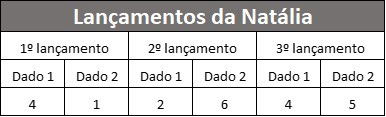
Estas são as pontuações de Pedro nos dois primeiros lançamentos:

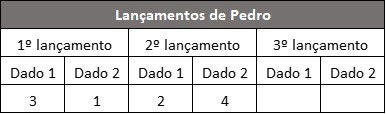
Quantos pontos, Pedro precisa no terceiro lançamento para vencer a partida?

Ver Resposta

Resposta: 11,99 pontos, ou seis em cada dado.

O jogo considera a média dos lançamentos, sendo assim, Natália obteve:

1º lançamento: 4 + 1 = 5
2º lançamento: 2 + 6 = 8
3° lançamento: 4 + 5 = 9

Calculando sua média, obtemos:

$numerador 5 espaço mais espaço 8 espaço mais espaço 9 sobre denominador 3 fim da fração igual a 22 sobre 3 aproximadamente igual 7 vírgula 33$

Assim, Pedro precisa de uma média maior que 7,33 pontos. Seus pontos nos dois primeiros lançamentos são:

1º lançamento: 3 + 1 = 4
2º lançamento: 2 + 4 = 6

Calculando a média e chamando de X a pontuação do terceiro lançamento, temos:

$numerador 4 espaço mais espaço 6 espaço mais espaço X sobre denominador 3 fim da fração igual a 7 vírgula 33 10 espaço mais espaço X espaço igual a espaço 3 espaço. espaço espaço 7 vírgula 33 espaço 10 espaço mais espaço X espaço igual a espaço 21 vírgula 99 X espaço igual a espaço 21 vírgula 99 espaço menos espaço 10 X espaço igual a espaço 11 vírgula 99$

Para vencer, Pedro de somar, pelo menos 11,99 pontos.

A única maneira de Pedro vencer a partida é tirando 6 nos dois dados.

Questão 7

(IF SUL — MG 2018) Celinho é o técnico do time de basquete de sua cidade. No seu time, os cinco titulares possuem altura média de 1,88 m. No campeonato que o time de Celinho vai disputar, os jogadores dos outros times têm, em média, 1,91 m. Para aumentar a altura média do seu time, Celinho tirou o jogador mais baixo do time, de altura de 1,79 m. Se quiser igualar à média de altura dos outros times, o jogador que entrará no time deverá ter altura igual a:

a) 1,88 m
b) 1,91 m
c) 1,94 m
d) 2,03 m

Ver Resposta

Resposta correta: c) 1,94 m.

Primeiros calculamos a média do time antes da substituição.

Média do time antes da substituição

$numerador a espaço mais espaço b espaço mais espaço c espaço mais espaço d espaço mais e espaço sobre denominador 5 fim da fração igual a 1 vírgula 88$

Onde, a, b, c, d, e, representam as alturas dos jogadores.

Considerando o jogador ,"e" , o mais baixo, com 1,79 m, substituímos este valor na média.

$numerador a espaço mais espaço b espaço mais espaço c espaço mais espaço d espaço mais espaço 1 vírgula 79 espaço sobre denominador 5 fim da fração igual a 1 vírgula 88$

Isolando as letras que representam as alturas oos outro jogadores:

$a espaço mais espaço b espaço mais c espaço mais espaço d igual a 1 vírgula 88 espaço. espaço 5 espaço menos espaço 1 vírgula 79 a espaço mais espaço b espaço mais c espaço mais espaço d igual a 9 vírgula 4 espaço menos espaço 1 vírgula 79 a espaço mais espaço b espaço mais c espaço mais espaço d igual a 7 vírgula 61$

Com isso, descobrimos a soma das alturas dos outros jogadores.

Média do time depois da substituição

Após a substituição a média deve ser, pelo menos, igual a 1,91.

Chamando de X a altura do novo jogador:

$numerador a espaço mais espaço b espaço mais c espaço mais espaço d espaço mais espaço X sobre denominador 5 fim da fração espaço igual a espaço 1 vírgula 91$

Resolvendo para X

$a espaço mais espaço b espaço mais espaço c espaço mais d espaço mais espaço X espaço igual a espaço 1 vírgula 91 espaço. espaço 5 a espaço mais espaço b espaço mais espaço c espaço mais d espaço mais espaço X espaço igual a 9 vírgula 55$

Já calculamos a soma a + b + c + d = 7,61

$a espaço mais espaço b espaço mais espaço c espaço mais espaço d espaço mais espaço X espaço igual a espaço 9 vírgula 55 7 vírgula 61 espaço mais espaço X espaço igual a espaço 9 vírgula 55 X espaço igual a espaço 9 vírgula 55 espaço menos espaço 7 vírgula 61 X espaço igual a espaço 1 vírgula 94$

Portando, a altura mínima do jogador novo, deverá ser 1,94 m.

Questão 8

(UFRGS — 2019) A média aritmética das idades de um grupo de 10 amigos é 22 anos. Ao ingressar mais um amigo nesse grupo, a média aritmética passa a ser de 23 anos. A idade do amigo ingressante no grupo, em anos, é

a) 29.
b) 30.
c) 31.
d) 32.
e) 33.

Ver Resposta

Resposta correta: e) 33.

A média com os 10 amigos é:

Onde,

i1, i2, ... ,i10 são as idades dos amigos.

Assim,

$i com 1 subscrito mais espaço i com 2 subscrito espaço mais espaço i com 3 subscrito espaço mais espaço i com 4 subscrito espaço mais espaço i com 5 subscrito mais espaço i com 6 subscrito espaço mais espaço i com 7 subscrito espaço mais espaço i com 8 subscrito espaço mais espaço i com 9 subscrito espaço mais espaço i com 10 subscrito espaço igual a espaço 22 espaço. espaço 10 espaço igual a espaço 220$

A média com os 11 amigos é:

$numerador i com 1 subscrito mais espaço i com 2 subscrito espaço mais espaço i com 3 subscrito espaço mais espaço i com 4 subscrito espaço mais espaço i com 5 subscrito mais espaço i com 6 subscrito espaço mais espaço i com 7 subscrito espaço mais espaço i com 8 subscrito espaço mais espaço i com 9 subscrito espaço mais espaço i com 10 subscrito espaço mais espaço i com 11 subscrito sobre denominador 11 fim da fração igual a 23 i com 1 subscrito mais espaço i com 2 subscrito espaço mais espaço i com 3 subscrito espaço mais espaço i com 4 subscrito espaço mais espaço i com 5 subscrito mais espaço i com 6 subscrito espaço mais espaço i com 7 subscrito espaço mais espaço i com 8 subscrito espaço mais espaço i com 9 subscrito espaço mais espaço i com 10 subscrito espaço mais espaço i com 11 subscrito espaço igual a espaço 23 espaço. espaço 11 espaço igual a espaço 253$

Substituindo a soma das idades dos amigos 1 ao 10 por 220 e, resolvendo para i11, temos:

$220 espaço mais espaço i com 11 subscrito igual a espaço 256 i com 11 subscrito igual a 253 espaço menos espaço 220 i com 11 subscrito igual a 33$

Portanto, a idade do amigo ingressante ao grupo é de 33 anos.

Questão 9

(CESGRANRIO — 2012) O valor da conta de telefone de Sebastião variou muito nos três primeiros meses de 2012. Em janeiro, Sebastião pagou R$ 48,50; em fevereiro, R$ 78,00 e em março, R$ 65,20. Qual foi, em reais, o valor mensal médio da conta telefônica de Sebastião no primeiro trimestre de 2012?

a) 60,60
b) 61,90
c) 62,20
d) 63,90
e) 64,20

Ver Resposta

Resposta correta: d) 63,90

Cálculo da média

$numerador 48 vírgula 5 espaço mais espaço 78 espaço mais espaço 65 vírgula 2 sobre denominador 3 fim da fração igual a numerador 191 vírgula 7 sobre denominador 3 fim da fração igual a 63 vírgula 9$

Portanto, R$ 63,90 foi o valor mensal médio da conta telefônica de Sebastião no primeiro trimestre de 2012.

Questão 10

Corretor de Redação para o Enem

Exercícios exclusivos

Estude sem publicidade

Continue praticando:

Siga aprendendo sobre:

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.