Mediana
Mediana é o número central de uma lista de dados organizados de forma crescente ou decrescente, sendo uma medida de tendência central ou, de centralidade.
A mediana é o valor do meio ou, que representa o meio, de uma lista de dados. Para mediana, a posição dos valores é importante, assim como a organização dos dados.
As medidas de tendência central ou de centralidade na estatística tem a função de caracterizar um conjunto de dados quantitativos, informando seu valor médio ou de posição central. Estes valores funcionam como um resumo que informam uma característica média geral dos dados.
À lista organizada de dados damos o nome de ROL, necessário para determinar a Mediana. Outras importantes medidas de centralidade são as médias e a moda, muito usadas em estatística.
Como se calcula a Mediana
Para calcular a mediana organizam-se os dados de forma crescente ou decrescente. Esta lista é o ROL de dados. Após, verificamos se a quantidade de dados no ROL é par ou ímpar.
Se a quantidade de dados no ROL é ímpar, a mediana é o valor do meio, da posição central.
Se a quantidade de dados no ROL é par, a mediana é a média aritmética dos valores centrais.
Exemplo 1 — mediana com quantidade ÍMPAR de dados no ROL.
Determine a mediana do conjunto A={12, 4, 7, 23, 38}.
Primeiro organizamos o ROL.
A={4, 7, 12, 23, 38}
Verificamos que a quantidade de elementos no conjunto A é ÍMPAR, sendo a mediana o valor do meio.
Portanto, a mediana do conjunto A é o 12.
Exemplo 2 — mediana com quantidade PAR de dados no ROL.
Qual a mediana das alturas dos jogadores de um time de vôlei onde as alturas são: 2,05m; 1,97m; 1,87m; 1,99m; 2,01m; 1,83m?
Organizando o ROL:
1,83m; 1,87m; 1,97m; 1,99m; 2,01m; 2,05m
Verificamos que a quantidade de dados é PAR. A mediana é a média aritmética dos valores centrais.
Portanto, a mediana das alturas dos jogadores é 1,98m.
Exercícios de Mediana
Exercício 1
(Enem 2021) O gerente de uma concessionária apresentou a seguinte tabela em uma reunião de dirigentes. Sabe-se que ao final da reunião, a fim de elaborar metas e planos para o próximo ano, o administrador avaliará as vendas, com base na mediana do número de automóveis vendidos no período de janeiro a dezembro.
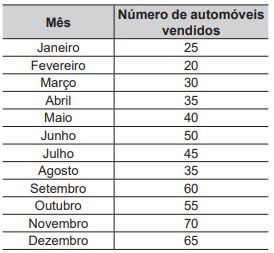
Qual foi a mediana dos dados apresentados?
a) 40,0
b) 42,5
c) 45,0
d) 47,5
e) 50,0
Exercício 2
(CEDERJ 2016) A tabela abaixo exibe as notas em quatro provas P1, P2, P3 e P4, de quatro alunos denominados por X, Y, Z e W.
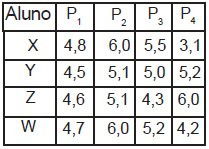
A menor mediana das quatro provas é a do aluno
a) X
b) Y
c) Z
d) W
Exercício 3
A seguinte distribuição de frequências se refere a uma pesquisa realizada por uma fábrica quanto à numeração de calças que seus operários usam com a finalidade de confecção de uniformes.
| Numeração de calças | Frequência (Número de operários) |
| 42 | 9 |
| 44 | 16 |
| 46 | 10 |
| 48 | 5 |
| 50 | 5 |
Sobre o exposto, assinale o que for correto.
A mediana das numerações de calças é 44.
Certo
Errado
Leia também:
Para mais sobre estatística:
- Estatística - Exercícios
- Exercícios de Média Aritmética
- Média Aritmética Ponderada
- Média Geométrica
- Medidas de Dispersão
- Desvio Padrão
- Variância e desvio padrão
- Frequência Relativa
- Frequência Absoluta
ASTH, Rafael. Mediana. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/mediana/. Acesso em:



