Desvio Padrão

Rosimar Gouveia

Professora de Matemática e Física

O desvio padrão é uma medida que expressa o grau de dispersão de um conjunto de dados. Ou seja, o desvio padrão indica o quanto um conjunto de dados é uniforme. Quanto mais próximo de 0 for o desvio padrão, mais homogêneo são os dados.

Como calcular o desvio padrão

O desvio padrão (DP) é calculado usando-se a seguinte fórmula:

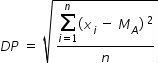
Sendo,

∑: símbolo de somatório. Indica que temos que somar todos os termos, desde a primeira posição (i=1) até a posição n
x_i: valor na posição i no conjunto de dados
M_A: média aritmética dos dados
n: quantidade de dados

Exemplo

Em uma equipe de remo os atletas possuem as seguintes alturas: 1,55 m ; 1,70 m e 1,80 m. Qual é o valor da média e do desvio padrão da altura desta equipe?

Cálculo da média, sendo n = 3

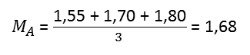
Cálculo do desvio padrão

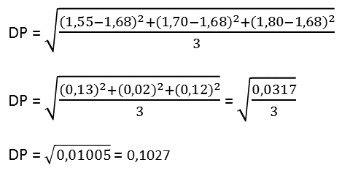
Leia também sobre Medidas de Dispersão.

Variância e Desvio Padrão

Variância é uma medida de dispersão e é usada também para expressar o quanto um conjunto de dados se desvia da média.

O desvio padrão (DP) é definido como a raiz quadrada da variância (V).

A vantagem de usar o desvio padrão ao invés da variância é que o desvio padrão é expresso na mesma unidade dos dados, o que facilita a comparação.

Fórmula da variância

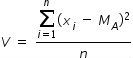
Saiba mais sobre Variância e Desvio padrão.

Exercícios Resolvidos

1) ENEM – 2016

O Procedimento de perda rápida de "peso" é comum entre os atletas dos esportes de combate. Para participar de um torneio, quatro atletas da categoria até 66 kg, Peso-Pena, foram submetidos a dietas balanceadas e atividades físicas. Realizaram três "pesagens" antes do início do torneio. Pelo regulamento do torneio, a primeira luta deverá ocorrer entre o atleta mais regular e o menos regular quanto aos "pesos". As informações com base nas pesagens dos atletas estão no quadro.

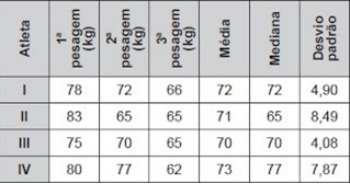
Após as três "pesagens", os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta.

A primeira luta foi entre os atletas

a) I e III.
b) I e IV.
c) II e III.
d) II e IV.
e) III e IV

2) ENEM – 2012

Um produtor de café irrigado em Minas Gerais recebeu um relatório de consultoria estatística, constando, entre outras informações, o desvio padrão das produções de uma safra dos talhões de sua propriedade. Os talhões têm a mesma área de 30 000 m² e o valor obtido para o desvio padrão foi de 90 kg/talhão. O produtor deve apresentar as informações sobre a produção e a variância dessas produções em sacas de 60 kg por hectare (10 000 m²). A variância das produções dos talhões expressa em (sacas/hectare)² é:

a) 20,25
b) 4,50
c) 0,71
d) 0,50
e) 0,25.

3) ENEM – 2010

Marco e Paulo foram classificados em um concurso. Para classificação no concurso o candidato deveria obter média aritmética na pontuação igual ou superior a 14. Em caso de empate na média, o desempate seria em favor da pontuação mais regular. No quadro a seguir são apresentados os pontos obtidos nas provas de Matemática, Português e Conhecimentos Gerais, a média, a mediana e o desvio padrão dos dois candidatos.
Dados dos candidatos no concurso

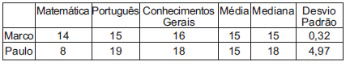
O candidato com pontuação mais regular, portanto mais bem classificado no concurso, é

a) Marco, pois a média e a mediana são iguais.
b) Marco, pois obteve menor desvio padrão.
c) Paulo, pois obteve a maior pontuação da tabela, 19 em Português.
d) Paulo, pois obteve maior mediana.
e) Paulo, pois obteve maior desvio padrão.

Pratique mais com:

• Exercícios de Desvio Padrão
• Exercícios sobre medidas de dispersão
• Exercícios de Média, Moda e Mediana
• Estatística - Exercícios
• Exercícios de Média Aritmética

Para saber mais, veja também:

• Média
• Média Aritmética Ponderada
• Média Geométrica
• Média, Moda e Mediana
• Estatística
• Frequência Relativa
• Tipos de Gráficos
• Gráfico de setores

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.