Prova de Matemática e Ciências da Natureza ENEM 2025 (com gabarito explicado)
Reunimos todas as questões da prova de Matemática e Ciências da Natureza do 2º dia do ENEM 2025, com gabarito oficial! Veja o gabarito da sua prova e refaça todas as questões com as explicações.
- Gabarito oficial - PROVA AZUL
- Gabarito oficial - PROVA AMARELA
- Gabarito oficial - PROVA CINZA
- Gabarito oficial - PROVA VERDE
Questão 91
A filtração em carvão é uma das mais antigas formas de purificação de água. O carvão ativado, diferentemente do carvão comum, é útil para ser empregado na remoção de material orgânico, cloro e outros contaminantes. Essa capacidade decorre de suas propriedades de adsorção. A origem do material utilizado para produzir o carvão ativado pode influenciar sua porosidade e, consequentemente, interferir na capacidade do material de remover impurezas. Na figura, é ilustrada esquematicamente a diferença entre as estruturas do carvão comum e do carvão ativado.
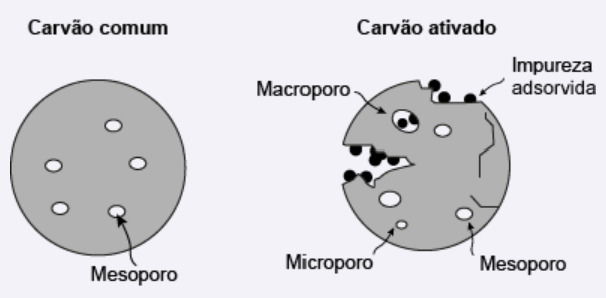
Qual característica do carvão ativado explica sua maior eficiência nesse processo?
A) Massa.
B) Dureza.
C) Densidade.
D) Superfície.
Condutividade.
Resposta correta: D) Superfície.
O carvão ativado funciona melhor que o carvão comum porque ele passa por um processo que cria muitos poros minúsculos em sua estrutura. Esses poros aumentam bastante a superfície de contato do material.
Pense assim: quanto mais “espaços” internos o carvão tiver, mais moléculas de sujeira, impurezas ou substâncias indesejadas poderão ficar aderidas à sua superfície. Esse fenômeno é chamado de adsorção, que é quando partículas ficam grudadas na superfície de um material.
Portanto, a grande eficiência do carvão ativado vem da superfície muito maior, e não de sua massa, dureza, densidade ou condutividade.
Questão 92
A maioria dos seres vivos tem um relógio biológico (ciclo circadiano), que regula as mudanças metabólicas e comportamentais de acordo com o ciclo de 24 horas de rotação da Terra. Em 2015, um artigo publicado na revista Science Advantage mostrou ser possível a transferência dos genes do relógio circadiano da cianobactéria Synechococcus elongatus para o genoma da bactéria Escherichia coli, um organismo não circadiano.
CHEN, A. H. et al. Transplantability of a Circardian Lock to Noncircardian Organism. Science Advantage, n. 1, 2015 (adaptado).
Estarão presentes no organismo geneticamente modificado os genes do
A) metabolismo de E. coli, apenas.
B) ciclo circadiano de E. coli, apenas.
C) metabolismo de S. elongatus e do ciclo circadiano de E. coli.
D) ciclo circadiano de S. elongatus e do metabolismo de E. coli.
E) ciclo circadiano de S. elongatus e do ciclo circadiano de E. coli.
Resposta correta: D) ciclo circadiano de S. elongatus e metabolismo de E. coli.
Quando usamos técnicas de engenharia genética, podemos “pegar” um gene de uma espécie e inseri-lo no DNA de outra.
No caso descrito, os cientistas transferiram para a E. coli os genes responsáveis pelo relógio biológico da cianobactéria Synechococcus elongatus. Isso significa que:
- A E. coli continua sendo ela mesma em suas funções normais, como crescimento e metabolismo.
- Mas passa a carregar também os genes que permitem o ciclo circadiano da outra espécie.
Assim, o organismo modificado terá:
- Metabolismo próprio da E. coli (porque isso não foi alterado);
- Genes do ciclo circadiano vindos de S. elongatus.
Questão 93
Os funcionários de um zoológico observaram um aumento na taxa de mortalidade de aves aquáticas por afogamento. Um grupo de biólogos analisou o comportamento das aves por várias semanas e observou que elas apresentavam dificuldade de flutuação, por causa do encharcamento das penas com água.
O aumento na taxa de mortalidade dessas aves estava associado a uma redução na
A) dilatação do papo.
B) reposição de penas das asas.
C) secreção da glândula uropigial.
D) formação da membrana natatória.
E) largura das cavidades de ossos pneumáticos.
Resposta correta: C) secreção da glândula uropigial
A maioria das aves possui uma glândula próxima à base da cauda chamada glândula uropigial. Ela produz uma substância oleosa que as aves espalham pelas penas enquanto se limpam.
Esse óleo tem uma função fundamental: impermeabilizar as penas. Sem essa proteção, a água penetra nas penas, elas ficam pesadas e a ave perde parte da sua capacidade de flutuar.
No caso descrito, as aves começaram a se afogar porque suas penas estavam ficando encharcadas. Isso indica que a produção da secreção impermeabilizante diminuiu, ou seja, houve redução na atividade da glândula uropigial.
Questão 94
Réguas elétricas são dispositivos que permitem a ligação segura e simultânea de dois ou mais aparelhos eletroeletrônicos à rede elétrica. Uma estudante comprou uma régua com seis tomadas, conforme a figura. Essa régua suporta uma intensidade máxima de corrente elétrica igual a 20 A. Acima desse valor, o fusível de segurança da régua se rompe, inutilizando-a até que um novo fusível seja instalado. Considere as potências nominais de alguns aparelhos eletroeletrônicos apresentadas no quadro.
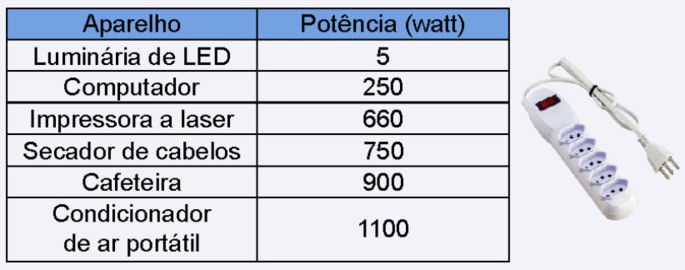
Em um dia quente, a estudante mantém o computador e o condicionador de ar portátil ligados à régua permanentemente. Nessa situação, ela tenta realizar algumas atividades, uma de cada vez, utilizando a mesma régua, na seguinte ordem:
1º – imprimir um trabalho escolar;
2º – fazer um café com a cafeteira;
3º – ligar a luminária;
4º – secar os cabelos.
Sabe-se que a régua foi ligada à tensão elétrica de 110 V, adequada para o funcionamento desses aparelhos.
Considerando a ordem das tentativas, quantas atividades a estudante conseguiu realizar sem queimar o fusível?
A) 4
B) 3
C) 2
D) 1
E) 0
Vamos por partes.
1. Qual é a potência máxima que a régua suporta?
A régua aguenta uma corrente de 20 A numa tensão de 110 V.
P = U × I
P = 110 × 20 = 2200 W
Essa é a potência total que pode estar ligada ao mesmo tempo sem estourar o fusível.
2. O que já está ligado?
- Computador: 250 W
- Ar-condicionado portátil: 1100 W
Consumo inicial: 250 + 1100 = 1350 W
Portanto, sobra:
2200 – 1350 = 850 W
Esse é o “espaço” disponível para ligar outros aparelhos.
3. Testando as atividades na ordem dada
1. Impressora (660 W)
- 660 W < 850 W → funciona sem problemas.
2. Cafeteira (900 W)
- 900 W > 850 W → ultrapassa o limite → queima o fusível imediatamente.
Como o fusível queima na segunda tentativa, nenhuma outra atividade pode ser realizada depois disso.
A estudante conseguiu apenas 1 atividade antes do fusível queimar.
Questão 95
TEXTO I
As mariposas
As mariposa, quando chega o frio
Fica dando volta em volta da lâmpida pra se esquentá. [sic]
BARBOSA, A. Reviva: Adoniran Barbosa. São Paulo: Som Livre, 2002 (fragmento).
TEXTO II
As mariposas se aproximam das lâmpadas atraídas pela luz, pois, sendo basicamente criaturas noturnas, estão adaptadas a seguir o brilho da lua, em um processo conhecido como orientação transversal. Assim, o que o sambista Adoniran Barbosa, no Texto I, descreve não é a causa, mas sim uma das consequências possíveis dessa aproximação. De fato, o calor gerado pelas lâmpadas, sobretudo as incandescentes, pode aquecer as mariposas.
HERTZBERG, R. Por que as mariposas são tão atraídas por luzes fortes? National Geographic, nov. 2020 (adaptado).
Nesse contexto, o processo de transferência de calor para as mariposas que independe da presença de fluidos é a
A) reflexão.
B) refração.
C) irradiação.
D) dispersão.
E) convecção.
Resposta correta: C) irradiação.
O calor pode ser transferido de três maneiras: condução, convecção e irradiação.
- Convecção depende do movimento de fluidos (ar ou água).
- Condução ocorre em sólidos quando há contato direto entre suas superfícies.
- Irradiação é a transferência de energia por ondas eletromagnéticas, como a luz ou o calor emitido pelo Sol, e não precisa de nenhum meio material para acontecer.
As mariposas se aproximam da lâmpada por causa da luz, e acabam recebendo calor da lâmpada principalmente por irradiação, porque o calor chega até elas na forma de radiação térmica.
Questão 96
Os sapinhos-ponta-de-flecha constituem um grupo de espécies encontradas na América Central e do Sul. Seus venenos são obtidos por meio do consumo de algumas formigas e cupins que se alimentam de plantas que contêm esses venenos. Esses anfíbios são usados para envenenar as flechas das zarabatanas dos caçadores nativos. Quando capturados e criados em condições artificiais, ou quando nascidos em cativeiro, não são tóxicos.
BADIO, B. et al. Epibatidine: Discovery and Definition as a Potent Analgesic and Nicotinic Agonist. Med. Chem. Res., n. 4, 1994 (adaptado).
A perda da capacidade de se obter a toxina nos nascidos em cativeiro é causada pela
A) diferença de umidade entre os ambientes.
B) ausência de alimentação natural.
C) adaptação ao novo ambiente.
D) mudança de comportamento.
E) variabilidade genética.
Resposta correta: B) ausência de alimentação natural.
Esses sapos não produzem o veneno sozinhos. Eles obtêm a toxina ao se alimentarem de certos insetos (formigas e cupins) que, por sua vez, comem plantas que contêm substâncias tóxicas.
Em cativeiro, esses sapinhos não recebem essa dieta específica. Como consequência, não conseguem acumular o veneno no corpo, e por isso não ficam tóxicos.
Portanto, a perda da toxicidade ocorre simplesmente porque eles não têm acesso aos mesmos alimentos que encontrariam na natureza.
Questão 97
A produção de vacinas exige uma sequência de procedimentos, além do cumprimento estrito de verificações de segurança. No esquema, estão demonstradas as etapas básicas realizadas para a fabricação de uma vacina utilizando a tecnologia tradicional e o efeito dela no organismo.
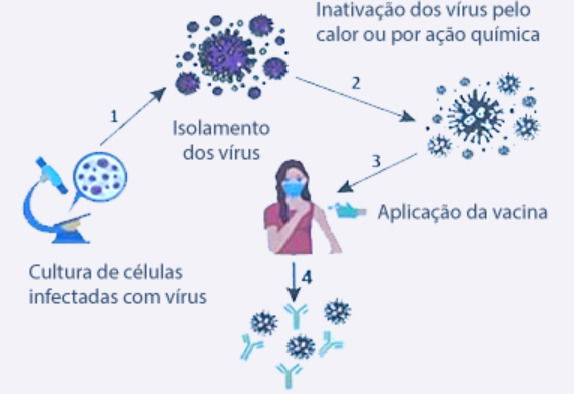
O antígeno utilizado na vacina causa um efeito protetor contra o vírus porque
A) mata o vírus pela ligação.
B) aglutina o vírus por associação.
C) contém imunoglobulinas de defesa.
D) induz a produção de proteínas neutralizadoras.
E) mantém a quantidade de anticorpos preexistentes.
Resposta correta: D) induz a produção de proteínas neutralizadoras.
As vacinas tradicionais apresentam ao corpo um vírus morto ou enfraquecido, ou alguma parte dele chamada antígeno. Esse antígeno não causa a doença, mas faz o sistema imunológico “treinar”, reconhecendo o invasor e reagindo.
O que acontece quando o antígeno entra no organismo?
Ele ativa o sistema imunológico, que começa a produzir:
- anticorpos, que são proteínas capazes de neutralizar o vírus real;
- e células de memória, que guardam a informação para o futuro.
Assim, se a pessoa vacinada encontrar o vírus verdadeiro depois, o corpo já sabe como reagir rapidamente.
Por isso, o antígeno protege porque estimula a produção de anticorpos, e não porque mata o vírus diretamente, aglutina partículas ou mantém anticorpos antigos.
Questão 98
O bioma Cerrado é caracterizado por apresentar ampla e natural diversidade de espécies vegetais. Nos últimos tempos, o homem vem modificando esse cenário pela inserção de plantas exóticas nesse ambiente. Exemplo disso é o cultivo do capim-gordura, nativo do continente africano e utilizado nesse tipo de ecossistema como forma de pastagem. É importante ressaltar que essa espécie vegetal é capaz de se espalhar por grandes áreas, devido à sua agressividade e poder competitivo.
CARLOS JR., L. A.; BARBOSA, N. P. U.; FERNANDES, G. W. O capim-gordura e as invasões no Cerrado brasileiro. Jornal do Biólogo, mar.-jun. 2008 (adaptado).
Em longo prazo, essa ação do homem pode gerar qual consequência?
A) Diversificar nichos ecológicos.
B) Assorear as nascentes do bioma.
C) Dificultar a infiltração de água na terra.
D) Diminuir as espécies nativas do bioma.
E) Contribuir com a redução das queimadas.
Resposta correta: D) Diminuir as espécies nativas do bioma.
O capim-gordura é uma planta exótica no Cerrado e, pior ainda, é uma espécie invasora. Isso quer dizer que:
- cresce rapidamente,
- se espalha com facilidade,
- usa muitos recursos (água, luz, nutrientes, espaço),
- e impede o desenvolvimento das plantas nativas.
Com o tempo, esse tipo de competição desigual faz com que as plantas originais do bioma percam espaço e diminuam em número.
Portanto, a consequência de longo prazo é a redução da biodiversidade local, ou seja, a diminuição das espécies nativas.
Questão 99
O monstro de gila, um lagarto encontrado em um deserto dos Estados Unidos, apresenta adaptações à falta de alimento nesse ambiente. Esse lagarto possui um hormônio que controla os níveis de açúcar em seu próprio sangue. Foi observado que esse hormônio também controla os níveis de açúcar no sangue de pessoas diabéticas.
RUSSELL, C. Ozempic e outros remédios inspirados em veneno de animais. Disponível em: www.bbc.com. Acesso em: 6 dez. 2024 (adaptado).
Considerando que animais de um mesmo grupo taxonômico podem apresentar características adaptativas semelhantes em ambientes similares, onde seria mais provável encontrar lagartos com essas características no território brasileiro?
A) Cerrado.
B) Pampas.
C) Caatinga.
D) Restinga.
E) Pantanal.
Resposta correta: C) Caatinga
O monstro de gila vive em um deserto dos Estados Unidos, um ambiente:
- quente,
- seco,
- com longos períodos sem água,
- e com baixa disponibilidade de alimento.
No Brasil, o bioma que mais se aproxima dessas condições é a Caatinga, que apresenta clima semiárido e espécies adaptadas a sobreviver em ambientes áridos — inclusive muitos répteis.
Assim, é nesse bioma que seria mais provável encontrar lagartos com adaptações semelhantes.
Questão 100
Existe um processo de purificação de água em que são removidos os sais dissolvidos. A água que passa por esse processo é muito utilizada em laboratórios de química, em indústrias (como solvente), em baterias de carro etc. Entretanto, esse tipo de água não é adequado para ingestão, pois pode causar problemas de saúde, como carência iônica e diarreia.
Essa água é chamada de
A) dura.
B) pesada.
C) sanitária.
D) destilada.
E) oxigenada.
Resposta correta: D) destilada.
Quando a água passa por destilação, ela é aquecida até virar vapor e, em seguida, resfriada para se tornar líquida novamente. Nesse processo:
- a água evapora,
- os sais minerais e outras substâncias não evaporam,
- e ficam para trás.
O resultado é uma água praticamente sem íons, muito pura — perfeita para uso em laboratórios, baterias, experimentos etc.
Mas, justamente por não ter minerais, não deve ser consumida, pois pode causar desequilíbrios no organismo.
Esse tipo de água é chamada de água destilada.
Questão 101
Por que os olhos ficam vermelhos em algumas fotografias?
Em fotos tiradas com câmeras fotográficas antigas, por vezes as pessoas aparecem com os olhos vermelhos. Isso ocorre porque a luz do flash da câmera incide diretamente no globo ocular, sendo refletida por uma região repleta de vasos sanguíneos.
Disponível em: www.uol.com.br. Acesso em: 14 jun. 2017 (adaptado).
Esse efeito é mais comum à noite ou em lugares pouco iluminados porque, com a pupila
A) dilatada, chega mais luz à retina.
B) retraída, chega mais luz vermelha à retina.
C) retraída, chega mais luz vermelha aos bastonetes.
D) retraída, chegam menos luzes azul e verde aos cones.
E) dilatada, chegam menos luzes azul e verde aos bastonetes.
Resposta correta: A) dilatada, chega mais luz à retina.
Quando estamos em um ambiente escuro, a pupila aumenta de tamanho (fica dilatada) para deixar entrar mais luz.
Quando o flash dispara, essa luz intensa entra rapidamente no olho e atinge uma região no fundo chamada retina, rica em vasos sanguíneos. A luz refletida por esses vasos volta para a câmera, gerando o efeito dos olhos vermelhos.
À noite ou em locais com pouca iluminação, como a pupila está mais aberta, mais luz do flash entra, e o efeito fica mais evidente.
Questão 102
O sashimi (filé de peixe cru) de baiacu é uma iguaria muito apreciada no Japão. Entretanto, sua ingestão pode causar a morte por parada respiratória, pois esse peixe contém uma potente neurotoxina termoestável, a tetrodotoxina, que é produzida e armazenada nas gônadas e vísceras.
Que ação poderia evitar essa intoxicação?
A) Criar os peixes em cativeiro.
B) Realizar a pesca com redes.
C) Consumir peixes cozidos ou fritos.
D) Preparar o peixe em condições adequadas de higiene.
E) Manusear o peixe sem provocar o rompimento dos órgãos internos.
Resposta correta: E) Manusear o peixe sem provocar o rompimento dos órgãos internos.
A toxina do baiacu, a tetrodotoxina, fica concentrada principalmente nas vísceras e nas gônadas.
Ela também é termoestável, o que significa que não é destruída pelo calor — portanto, cozinhar ou fritar não elimina o risco.
Para evitar a contaminação da carne consumida no sashimi, é essencial:
- não romper os órgãos internos durante o preparo,
- evitando que a toxina se espalhe pelos músculos, que são a parte ingerida.
Por isso, somente um manuseio extremamente cuidadoso evita a intoxicação.
Questão 103
A deficiência da enzima lipase ácida causa uma doença em que o portador apresenta células que não degradam colesterol esterificado nem triglicerídeos, resultando no depósito desses compostos em diversos órgãos, principalmente no fígado.
ANDERSON, R. A. et al. In Situ Localization of the Geneticc Locus Encoding [...]. Genomics, n.1, jan. 1993 (adaptado).
Essa doença resulta da insuficiência funcional de qual estrutura celular?
A) Lisossomos.
B) Ribossomos.
C) Mitocôndrias.
D) Peroxissomos.
E) Retículo endoplasmático liso.
Resposta correta: A) Lisossomos.
Os lisossomos são organelas especializadas em digestão celular. Eles contêm várias enzimas, entre elas a lipase ácida, responsável por quebrar lipídios, como:
- triglicerídeos
- colesterol esterificado
Se essa enzima não funciona, a célula não consegue degradar essas gorduras, que começam a se acumular, especialmente no fígado. Esse acúmulo caracteriza doenças de armazenamento lisossomal.
Assim, o problema está diretamente ligado ao mau funcionamento dos lisossomos.
Questão 104
A quantidade de CO₂ na atmosfera da Terra aumentou em 50%, e a temperatura está agora cerca de 1,2 °C mais quente em comparação ao século XIX. O ritmo de aumento da temperatura precisa diminuir se quisermos evitar as piores consequências das mudanças climáticas. Cientistas afirmam que o aquecimento global precisa ser mantido em 1,5 °C até o ano 2100. No entanto, a menos que outras ações sejam tomadas, o planeta ainda pode aquecer mais de 2 °C até o final deste século. Na prática, os países precisam enfrentar as mudanças climáticas com ações mitigadoras, que reduzam tanto as emissões quanto os níveis de CO subscript 2 na atmosfera.
Um guia rápido para entender as mudanças climáticas. Disponível em: www.bbc.com. Acesso em: 6 dez. 2021 (adaptado).
Qual ação mitigadora auxilia na remoção desse gás presente na atmosfera, reduzindo seus níveis?
A) Plantar mais árvores.
B) Instalar mais usinas eólicas.
C) Ampliar o uso de energia solar.
D) Manter os combustíveis fósseis no solo.
E) Produzir menos resíduos sólidos urbanos.
Resposta correta: A) Plantar mais árvores.
Árvores removem CO₂ do ar por meio da fotossíntese. Nesse processo, elas:
- absorvem dióxido de carbono,
- transformam o carbono em matéria orgânica (tronco, folhas, raízes),
- e liberam oxigênio.
Portanto, o plantio de árvores é uma ação mitigadora porque retira CO₂ da atmosfera, diminuindo sua concentração.
Outras alternativas reduzem emissões, mas não removem diretamente o gás já presente no ar.
Questão 105
As usinas termonucleares produzem energia elétrica a partir da energia térmica gerada em reações nucleares. Normalmente, essas usinas funcionam por meio de dois circuitos, denominados circuito primário (vaso de pressão, pressurizador e bomba) e circuito secundário (gerador de vapor, turbina, condensador, tanque de alimentação e bombas), além de um sistema de água de refrigeração, formado por uma bomba ligada a uma fonte hídrica natural.
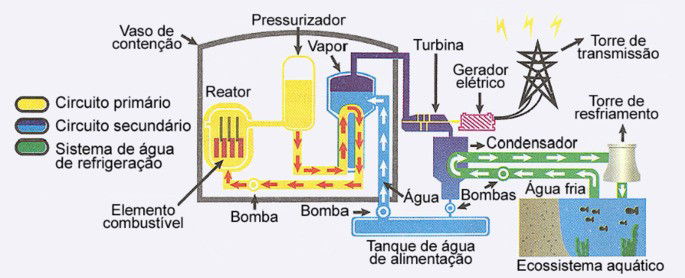
Durante a operação, se o sistema de água de refrigeração funcionar de forma ineficiente pode causar poluição térmica, comprometendo a vida no ecossistema aquático.
Disponível em: www.eletronuclear.gov.br. Acesso em: 29 nov. 2021 (adaptado)
Para o ecossistema aquático, a ineficiência do sistema de água de refrigeração tem como consequência a
A) diminuição do pH.
B) liberação de gases poluentes.
C) contaminação por combustíveis.
D) liberação de elementos radioativos.
E) diminuição da solubilidade do gás oxigênio.
Gabarito: E
O sistema de água de refrigeração mantém a temperatura do circuito secundário sob controle.
Se o sistema funcionar de forma ineficiente, a água devolvida ao ecossistema estará mais quente.
A temperatura elevada diminui a solubilidade do oxigênio na água, pois quanto maior a temperatura dela, menor a solubilidade de qualquer que seja o gás, prejudicando a vida aquática.
Questão 106
No início do século XX, as fórmulas das substâncias eram representadas de modo diferente do atual. A figura apresenta uma fotografia bem antiga (1909) que registra uma aula de química ministrada em um colégio em Santos (SP). Um olhar mais atento permite identificar como os compostos químicos eram representados.

O nitrogênio era chamado de azoto e representado pelo símbolo Az. Vê-se na lousa a equação representativa da adição do oxigênio atômico (O) ao monóxido de nitrogênio (AzO) com a formação de dióxido de nitrogênio (AzO²). Analogamente, o nitrato de sódio era representado por NaAzO³.
Disponível em: www.novomilenio.inf.br. Acesso em: 29 ago. 2014 (adaptado).
Em 1909, as representações das substâncias ácido nítrico e cloreto de cálcio, tendo por base essas informações e seguindo a mesma lógica, seriam, respectivamente:
A) HAzO³ e CaCl²
B) HAz³O e Ca²Cl
C) H³AzO⁴ e CaCl
D) HAz³O e KCl²
E) HAzO² e KCl
Resposta correta: A) HAzO³ e CaCl²
A lógica da época era:
- nitrogênio era chamado de azoto (Az);
- fórmulas eram escritas com o mesmo número de oxigênios e halogênios que usamos hoje, mas com símbolos diferentes.
Vamos aplicar isso:
1. Ácido nítrico — fórmula moderna: HNO₃
- N (nitrogênio) → Az
- O₃ permanece O³
Fica então: HAzO³
2. Cloreto de cálcio — fórmula moderna: CaCl₂
- Ca permanece Ca
- Cl₂ permanece Cl²
Portanto: CaCl²
Questão 107
A figura apresenta a herança genética de uma característica a partir do cruzamento de insetos de uma mesma espécie.
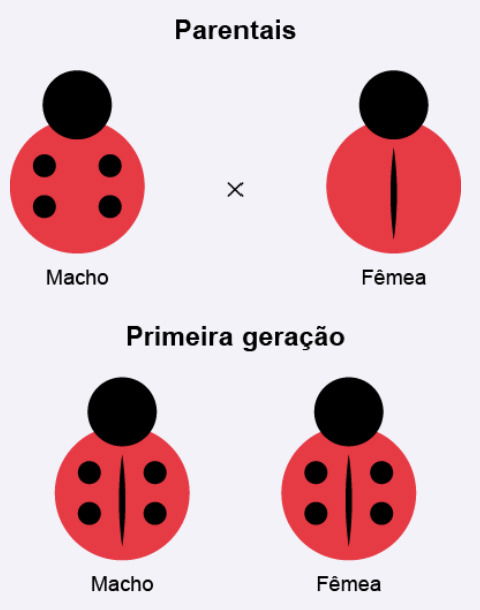
Qual alternativa representa a proporção fenotípica da prole resultante do cruzamento entre indivíduos da primeira geração?
A) 
B) 
C) 
D) 
E) 
O cruzamento parental envolve dois fenótipos diferentes, cada um com um alelo distinto (A₁A₁ e A₂A₂).
A F₁ apresenta 100% A₁A₂, e como ambas as características aparecem juntas nos descendentes, conclui-se que se trata de codominância.
Cruzando dois heterozigotos da F₁ (A₁A₂ × A₁A₂):
| Genótipo | Proporção | Fenótipo |
|---|---|---|
| A₁A₁ | 25% | bolinhas |
| A₁A₂ | 50% | bolinhas + risco |
| A₂A₂ | 25% | risco |
Logo, a proporção fenotípica é 1 : 2 : 1, correspondendo a:
1 joaninha com 4 bolinhas, 1 com risco vertical e 2 com bolinhas e risco.
Questão 108
Para transportar uma caixa do primeiro para o segundo piso de uma construção, um trabalhador precisará arrastá-la sobre um plano inclinado. O trabalhador começa a arrastar a caixa no primeiro piso, exercendo sobre ela uma força de grande intensidade, paralela ao seu deslocamento. Na medida em que a caixa sobe o plano inclinado, ele decide reduzir a força sobre ela, arrastando-a lentamente até chegar ao segundo piso. Considere que a caixa permanece em movimento nos encontros dos pisos com o plano inclinado, e que a rugosidade entre as superfícies permanece a mesma durante todo o percurso.
O comportamento da força de atrito entre a caixa e o chão no plano inclinado é representado em:
A) 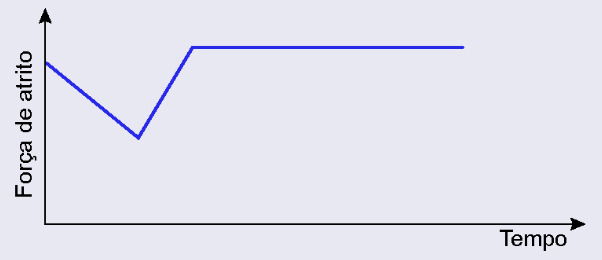
B) 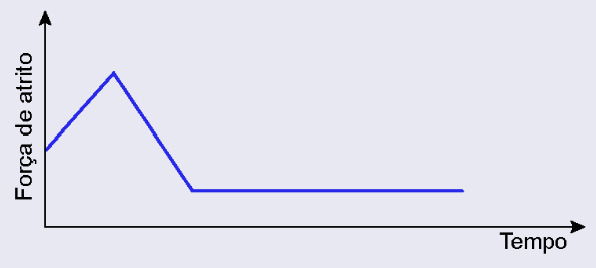
C) 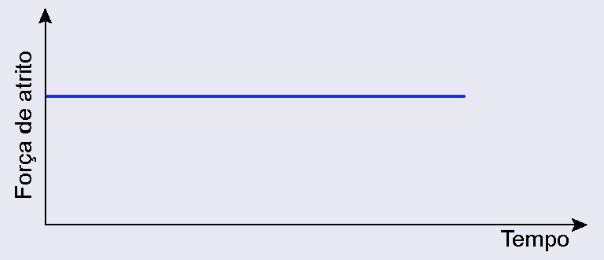
D) 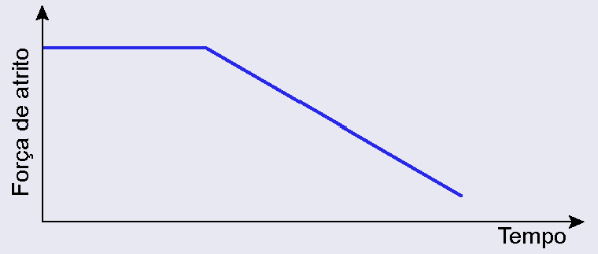
E) 
A questão analisa apenas o trecho do plano inclinado, e a caixa já está em movimento durante todo esse percurso.
Para atrito cinético (dinâmico):
No plano inclinado, tanto o coeficiente de atrito quanto a força normal permanecem constantes.
Portanto, a força de atrito também é constante, resultando em um gráfico linear e horizontal.
Questão 109
O fruto do cajueiro é um aquênio repleto de um líquido escuro, quase preto, cáustico e inflamável. Esse líquido da casca da castanha do caju (LCC) representa aproximadamente 25% da massa da castanha e é um subproduto de agronegócio do caju. Quando submetido a altas temperaturas, o ácido anacárdico presente no LCC é convertido a cardanol, que recebe a denominação de LCC técnico, conforme o esquema:
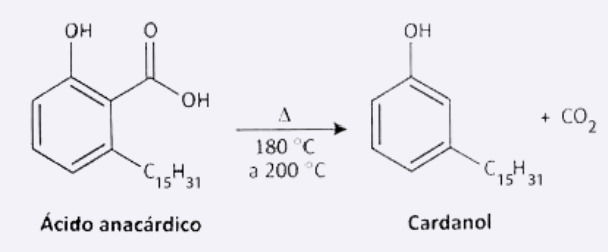
MAZZETTO, S. E.; LOMONACO, D.; MELE, G. Óleo da castanha de caju: oportunidades e desafios no contexto do desenvolvimento e sustentabilidade industrial. Química Nova, n. 3, 2009 (adaptado).
O LCC técnico é produzido por meio de uma reação orgânica do tipo:
A) hidrólise.
B) fenilação.
C) esterificação.
D) hidrogenação.
E) descarboxilação.
Gabarito: E
Ao aquecer o ácido anacárdico (ácido carboxílico) entre 180–200 °C, ocorre a remoção do grupo carboxila (–COOH), liberando CO₂ e formando cardanol.
Isso caracteriza uma reação de descarboxilação.
Questão 110
A química nuclear é uma importante ferramenta na produção de substâncias utilizadas na área da saúde humana. A radiação emitida pelo cobalto-60 é utilizada na medicina como ferramenta de diagnóstico e no tratamento do câncer. No entanto, esse radioisótopo tem um tempo de armazenamento limitado, pois seu tempo de meia-vida é de 5,3 anos. Considere um frasco como uma amostra contendo 2,00 mg de cobalto-60, armazenado durante um período de 26,5 anos.
A massa do cobalto-60, em miligrama, que restará ao final desse tempo é mais próxima de:
A) 2,00 mg.
B) 1,00 mg.
C) 0,40 mg.
D) 0,13 mg.
E) 0,06 mg.
Gabarito: E
Meia-vida do Co-60: 5,3 anos
Tempo total: 26,5 ÷ 5,3 = 5 meias-vidas
Aplicando o decaimento e reduzindo a quantidade sempre à metade:
Aproximando: 0,06 mg.
Questão 111
O esquema apresenta as etapas do processo de biodigestão, uma forma de dar um destino saudável a excrementos animais e restos de comida produzidos em áreas de criação de gado e porcos confinados.
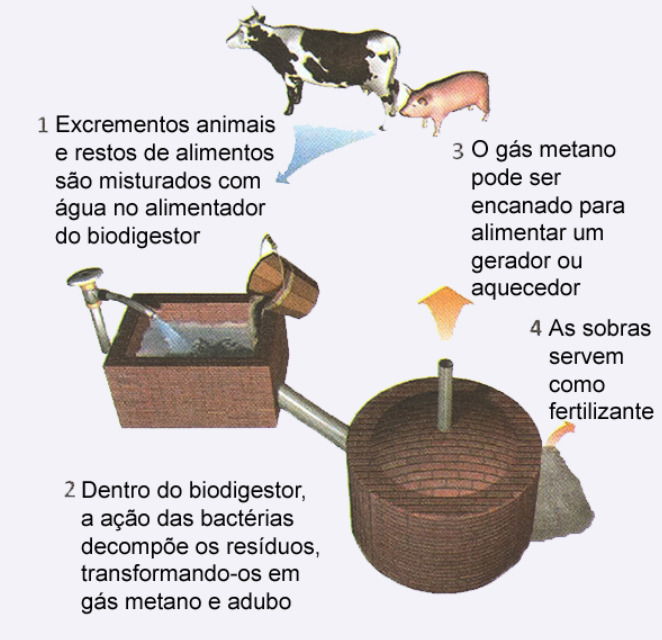
Dar destino sustentável às sobras, conforme apresentado na etapa 4, ajuda a evitar a:
A) bioacumulação de toxinas em plantas
B) eutrofização dos corpos de água
C) destruição da camada de ozônio
D) ocorrência de inversão térmica
E) produção de chuva ácida
Gabarito: B
O processo de biodigestão evita que efluentes ricos em nitrogênio e fósforo sejam descartados em rios e lagos.
Quando tais nutrientes chegam à água, promovem:
Eutrofização — crescimento excessivo de algas e diminuição de O2 dissolvido devido à alta população desta espécie. Com a diminuição de O2, essas algas morrem e dão espaço à micro-organismos anaeróbios e patogênicos.
A etapa 4 do esquema previne exatamente esse processo.
Questão 112
Golden Rice, ou arroz dourado, é uma variedade de arroz enriquecida em betacaroteno, precursor da vitamina A. Foi desenvolvida para ajudar a combater a doença decorrente da deficiência dessa vitamina. Para a obtenção dessa variedade de arroz, foram utilizados métodos de engenharia genética.
BORÉM, A.; SANTOS, F. R. Entendendo a biotecnologia. Viçosa: UFV, 2008 (adaptado).
Esse alimento contribui para diminuir a carência associada a qual doença?
A) Hemofilia.
B) Escorbuto.
C) Raquitismo.
D) Cegueira noturna.
E) Anemia perniciosa.
Gabarito: D
O Golden Rice é enriquecido com betacaroteno, precursor da vitamina A.
A deficiência dessa vitamina está ligada à cegueira noturna (nictalopia), causada pela baixa produção de pigmentos essenciais à visão em baixa luminosidade.
Questão 113
A Figura 1 apresenta o esquema de um tubo de imagem em que um filamento, na posição A, libera elétrons por efeito termiônico. Esses elétrons formam um feixe estreito, que é acelerado por campos elétricos em direção à parte interna da tela. Nesse caminho, o feixe de elétrons passa por outro campo elétrico, na região B, atingindo, em seguida, a parte interna da tela do tubo, a qual é recoberta por um material que emite luz ao receber o impacto dos elétrons.
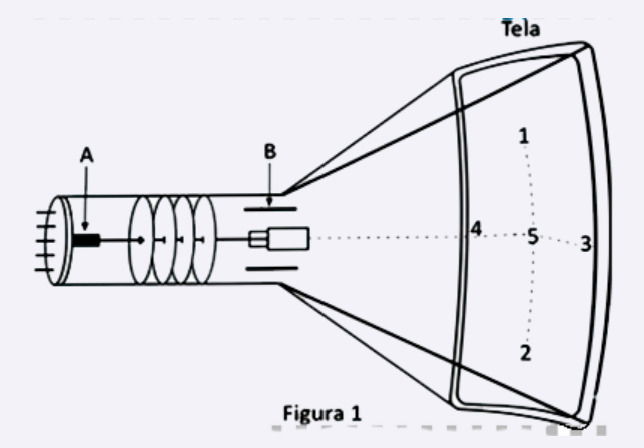
Na Figura 2, a carga negativa representa o feixe de elétrons que é acelerado e, posteriormente, atinge um ponto da tela. O campo elétrico na região B apresenta a seguinte configuração:
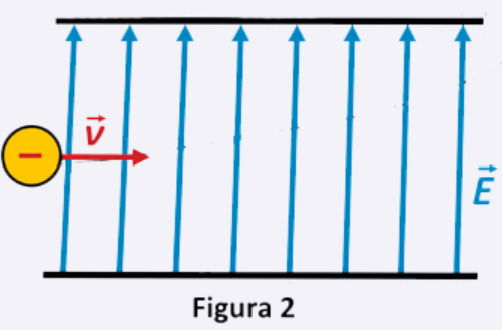
Nessa situação, qual ponto da tela será atingido pelo feixe de elétrons?
A) 1
B) 2
C) 3
D) 4
E) 5
Gabarito: B
No tubo de imagem:
- O filamento A libera elétrons por efeito termiônico.
- Os elétrons são acelerados por campos elétricos e seguem em direção à tela.
- Ao passar pela região B, existe um campo elétrico perpendicular ao movimento.
A força elétrica é dada por:
Para cargas negativas temos:
- A força elétrica atua na direção do campo, mas em sentido oposto à direção do campo se a carga for negativa.
- Assim, o feixe de elétrons será desviado para baixo (verticalmente), atingindo o ponto 2 da tela.
Questão 114
A tirinha ilustra um processo físico em que a onda sonora, produzida pela Mônica, causa a quebra das taças de cristal. O fenômeno ondulatório que provoca a quebra das taças só é possível em razão de uma característica da voz produzida pela Mônica naquele momento, que, diferentemente do que sugere a tirinha, não está relacionada à sua intensidade.

Esse fenômeno e a característica associada à voz da Mônica são, respectivamente:
A) reflexão e comprimento de onda.
B) ressonância e frequência.
C) interferência e velocidade.
D) ressonância e timbre.
E) reflexão e amplitude.
Gabarito: B
O fenômeno físico envolvido: ressonância.
- Para quebrar uma taça, a frequência da voz deve corresponder à frequência natural de vibração da taça.
- Não depende da intensidade, mas sim da frequência correta.
Portanto, a característica da voz é a frequência, e o fenômeno é ressonância.
Questão 115
Em uma aula prática de química orgânica, um professor identificou os frascos de várias substâncias apenas por suas fórmulas moleculares. Em seguida, apresentou a representação tridimensional da molécula do borneol, um álcool secundário, conforme a figura. Ele explicou que, quando oxidado, o borneol dá origem à cânfora, uma cetona usada desde a Antiguidade como incenso e no preparo de medicamentos. Finalmente, o professor solicitou que os alunos identificassem o frasco contendo a substância cânfora.
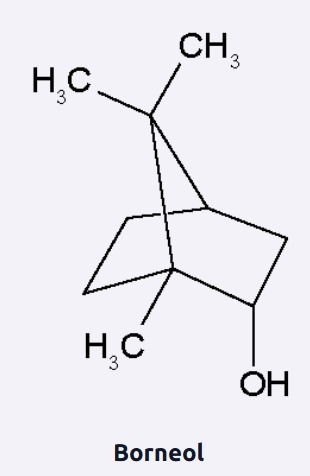
O frasco contendo cânfora apresenta a fórmula molecular:
A) C₉H₁₆O
B) C₉H₁₇O
C) C₁₀H₁₆O
D) C₁₀H₁₆O₂
E) C₁₀H₁₈O₂
Gabarito: C
Borneol: álcool secundário.
Oxidação de álcool secundário → cetona.
Neste tipo de oxidação, a molécula oxidada perde 2 hidrogênios pela eliminação de H2O onde há a hidroxila. Assim, se encontrarmos a fórmula molecular do borneol que que é C10H18O, apenas removemos 2 hidrogênios para chegarmos à cânfora, cuja fórmula molecular é C10H16O.
Questão 116
As cangas são ambientes resultantes da atuação, ao longo de milhões de anos, de chuvas, enxurradas, calor e ventos em rochas ricas em ferro. São compostas por até 90% de óxidos de ferro e contêm solos muito ácidos, rasos, com reduzidos índices de fertilidade e temperaturas que atingem quase 70 °C na superfície. Ao contrário do que se imagina, esse tipo de ambiente abriga comunidades de plantas e animais com elevado número de espécies e distribuição restrita.
CARMO, F. F. et al. Ilhas de ferro estratégicas para a conservação.
Disponível em: http://cienciahoje.org.br.
Acesso em: 2 dez. 2018 (adaptado).
A seleção adaptativa nesses ambientes favorece a ocorrência de espécies:
A) exóticas
B) migratórias
C) endêmicas
D) dominantes
E) generalistas
Gabarito: C
Cangas: ambientes hostis com solos ácidos, rasos e temperaturas elevadas.
Apesar do número de espécies ser alto, elas têm distribuição restrita, pois estão adaptadas às condições específicas das cangas.
Espécies que vivem em regiões específicas são endêmicas, pois são encontradas apenas naquele local.
Questão 117
Para a produção de titânio metálico ou dióxido de titânio puros, é necessário fazer a cloração do minério que contém dióxido de titânio, com o objetivo de separar esse óxido de outras substâncias presentes no minério. A principal reação química de cloração é representada por:
![]()
Depois da cloração, o tetracloreto de titânio é condensado e convertido, novamente, a dióxido de titânio.
Após o sistema atingir o equilíbrio químico, como a formação do TiCl₄ pode ser favorecida?
A) Aumentando a pressão total do sistema.
B) Diminuindo a temperatura do sistema.
C) Aumentando a pressão parcial de O₂.
D) Aumentando a pressão parcial de Cl₂.
E) Variando a quantidade de TiO₂.
Gabarito: D
Reação de cloração do TiO₂: TiO₂ + 2 Cl₂ + C → TiCl₄ + CO₂.
Para favorecer a formação de TiCl₄ em equilíbrio, devemos aumentar a quantidade de reagentes, neste caso, o Cl2:
Aumentar a pressão parcial de Cl₂ → reação direta é favorecida.
Questão 118
A laje de um depósito de bebidas tem 50 m² de área útil de armazenamento e foi projetada para suportar pressões de até 10⁴ Pa. O gerente pretende armazenar um produto cuja densidade é 1 250 kg/m³. Considere a aceleração da gravidade igual a 10 m/s².
A altura máxima, em metro, de empilhamento do produto que essa laje é capaz de suportar é?
A) 0,16 m.
B) 0,50 m.
C) 0,80 m.
D) 1,60 m.
E) 8,00 m.
Gabarito: C
- Dados:
- Área: A = 50m²
- Pressão máxima: P = 104 Pa
- Densidade: ρ = 1250kg/m³
- Gravidade: g = 10m/s²
Cálculo:
Questão 119
Em uma comunidade rural, os moradores utilizam uma bomba-d’água alimentada por 100 V de tensão contínua, podendo variar em até 5 V. Um eletrotécnico pretende instalar placas fotovoltaicas para alimentar essa bomba. As placas são idênticas e cada uma apresenta tensão de operação igual a 34 V com corrente de 7,5 A. Além disso, cada placa apresenta 40 V de tensão elétrica, quando em circuito aberto. Assim, considerando que a placa descrita é um gerador não ideal, em circuito aberto ela pode ser representada conforme a figura:
O eletrotécnico construiu um circuito que permite à bomba-d’água operar corretamente com o menor número possível de placas conectadas. Para isso, desenhou um diagrama no qual todas essas placas são representadas como um único gerador não ideal, com a especificação das correspondentes características elétricas.
O diagrama que representa o circuito construído pelo eletrotécnico é:
A) 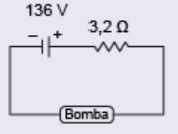
B) 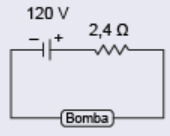
C) 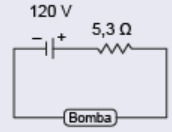
D) 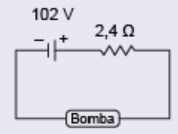
E) 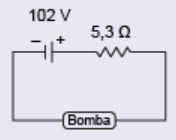
Gabarito: B
Placa:
Tensão mínima da bomba: 95 V → número mínimo de placas: 3
Tensão total das 3 placas: 34 × 3 = 102V (dentro do limite 100–105 V)
Questão 120
A figura ilustra as informações contidas no manual de um sistema de alarme que utiliza transmissores e receptores de radiação eletromagnética para a detecção de movimento. O receptor é regulado pelo tempo de resposta, que corresponde ao intervalo necessário para o corpo do invasor atravessar completamente o feixe de diâmetro d = 15 cm. Considere que a menor porção do corpo de um invasor é a sua posição de perfil, cuja espessura típica é 20 cm. São indicados cinco possíveis movimentos de um invasor e suas velocidades típicas, que devem ser observadas para a escolha do tempo de resposta.
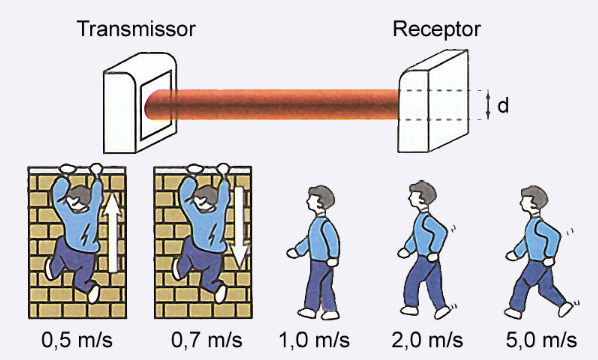
Nesse sistema, o menor tempo de resposta, em milissegundo, que garante a detecção de um possível invasor é mais próximo de
A) 30 ms.
B) 70 ms.
C) 300 ms.
D) 400 ms.
E) 700 ms.
Dados:
- Feixe: d = 15cm = 0,15m
- Espessura mínima do invasor: 20 cm = 0,2m
Para a pessoa ultrapassar completamente o sensor ela tem que se deslocar:
- deslocamento total = 0,15 + 0,2 m = 0,35 m
- Velocidade máxima: v = 5m/s
Cálculo:
Questão 121
A dimetilamina é uma substância de elevada toxidez que entra em ebulição a 7 °C. Na madrugada de um dia frio, essa substância se espalhou por uma rodovia após um acidente de trânsito envolvendo um caminhão que transportava esse produto. Para minimizar a agressão ao meio ambiente, bem como evitar a evaporação da dimetilamina com a elevação da temperatura ao longo do dia, um químico considerou o uso de algumas substâncias ou misturas como água, vinagre, óleo de soja, sal de cozinha e bicarbonato de sódio.
Dentre as opções apresentadas, o tratamento correto para minimizar esse problema é usar
A) água.
B) vinagre.
C) óleo de soja.
D) sal de cozinha.
E) bicabornato de sódio.
Resposta correta: B) vinagre
A dimetilamina é uma base (alcalina). Isso acontece porque o nitrogênio na sua molécula tem um par de elétrons não ligados, que pode aceitar prótons (H⁺).
Bases e ácidos podem reagir entre si em uma neutralização, formando um sal.
O vinagre é uma solução de ácido acético (ácido fraco). Quando aplicado sobre a dimetilamina, ele reage quimicamente com a amina, formando um sal que é menos volátil e menos perigoso.
As outras opções não provocam essa reação química:
- Água só dilui, não neutraliza.
- Óleo, sal ou bicarbonato não reagem da mesma forma ou são menos eficazes nesse caso.
Questão 122
O aquecimento em fogões por indução utiliza bobinas para produzir um campo magnético variável. Essa bobina se localiza abaixo do vidro cerâmico sobre o qual a panela se apoia. O mecanismo aquece apenas a panela que se encontra na zona de cozimento, o que é uma das principais vantagens em relação ao uso do fogão a gás ou de resistência elétrica.
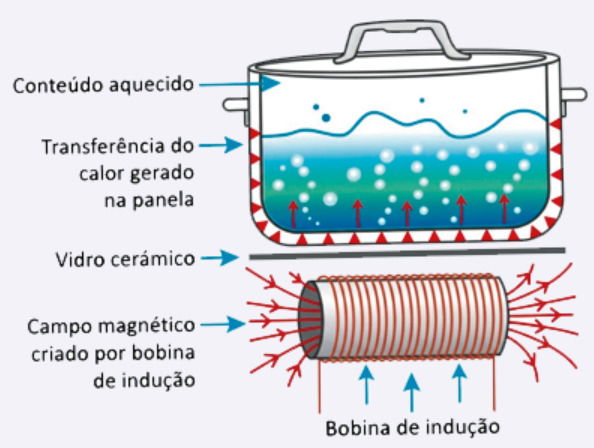
O uso do campo magnético variável tem a finalidade de
A) imantar o material da panela por indução.
B) movimentar os átomos de ferro concentrados no fundo da panela.
C) emitir radiação eletromagnética, aquecendo a panela através do vidro cerâmico.
D) induzir corrente elétrica na parte inferior da panela, aquecendo-a por efeito Joule.
E) gerar um fluxo de corrente de convecção no ar contido entre a região da bobina e o vidro cerâmico.
Resposta correta: D) induzir corrente elétrica na parte inferior da panela, aquecendo-a por efeito Joule.
O fogão por indução usa bobinas de metal abaixo do vidro para gerar um campo magnético variável.
Esse campo não aquece diretamente a panela; ele induz correntes elétricas na base metálica da panela.
A corrente elétrica que circula na panela gera calor por efeito Joule (o mesmo princípio do chuveiro elétrico, mas localizado na panela).
Assim, apenas a panela aquece, e o vidro acima dela permanece relativamente frio.
Outras alternativas estão incorretas porque:
- A panela não é “imantada” permanentemente.
- Os átomos de ferro não se movem individualmente; quem gera calor é a corrente elétrica induzida.
- Não há radiação significativa nem convecção de ar entre a bobina e o vidro.
Resumo para memorizar: indução → corrente elétrica na panela → calor.
Questão 123
Plantas e algas realizam fotossíntese oxigênica para síntese de matéria orgânica e, para isso, utilizam trifosfato de adenosina (ATP) e nicotinamida adenina dinucleotídeo fosfato reduzido (NADPH). Já algumas bactérias fotossintetizantes não apresentam cloroplasto e clorofila, mas um pigmento denominado bacterioclorofila. Esses procariotos realizam a fotossíntese anoxigênica, um processo de síntese de matéria orgânica utilizando o gás carbônico (CO2) e o gás sulfídrico (H2S).
Na fotossíntese oxigênica, qual composto desempenha função análoga à do H2S?
A) ATP.
B) NADPH.
C) Oxigênio.
D) Clorofila.
E) Água.
Resposta correta: E) Água.
Em fotossíntese anoxigênica (bactérias sulforosas):
- O H₂S doa elétrons (e⁻) e íons H⁺ para a cadeia de transporte de elétrons, permitindo a síntese de moléculas orgânicas.
- O enxofre (S) é liberado como subproduto, formando gás sulfídrico
Em fotossíntese oxigênica (plantas, algas, cianobactérias):
O H₂O exerce o mesmo papel que o H₂S: fornece elétrons e íons H+.
O oxigênio (O₂) é liberado como subproduto.
Portanto, a água é o equivalente do H₂S nas plantas.
Resumo para memorizar:
- Fotossíntese oxigênica → H₂O doa e⁻ → O₂ sai.
- Fotossíntese anoxigênica → H₂S doa e⁻ → S sai.
Questão 124
Objetos de prata escurecem em contato com compostos contendo enxofre por causa da formação de uma fina camada de sulfeto de prata. Um método simples para clarear o objeto consiste em forrar um recipiente com papel alumínio, adicionar ao recipiente uma solução aquosa de cloreto de sódio e, enfim, mergulhar o objeto de prata enegrecido. Em cerca de três minutos, a prata volta à coloração original. As seguintes semirreações e os respectivos potenciais-padrão de redução são úteis para a compreensão dos fenômenos ocorridos.
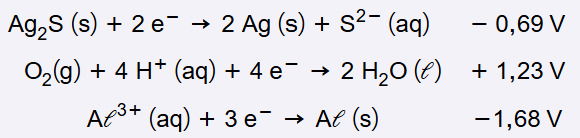
Os valores das diferenças de potencial-padrão das reações que representam o escurecimento e o clareamento do objeto de prata são, respectivamente:
A) +0,54 V e +2,37 V.
B) +1,92 V e +0,99 V.
C) −0,15 V e +5,43 V.
D) +2,61 V e +1,29 V.
E) +0,15 V e −1,29 V.
Resposta correta: B) +1,92 V e +0,99 V.
1. Escurecimento da prata:
- Quando a prata entra em contato com enxofre, forma Ag₂S, que escurece o objeto.
- Essa reação envolve oxidação da prata (Ag → Ag⁺) e tem um potencial-padrão positivo de cerca de +0,69 V. Veja que este processo é o inverso do fornecido na questão e, por isso, o sinal do potencial muda.
- Quando a prata oxida, fornece elétrons para o O2 que reduz de acordo com a segunda semi-reação da questão, com potencial +1,23V.
- Somando estes potenciais, temos +0,69V + 1,23V = +1,92V
2. Clareamento com papel alumínio e sal:
- O papel alumínio atua como agente redutor, ou seja, doa elétrons para o sulfeto de prata. A reação para o alumínio então está invertida na questão, tendo o seu potencial de oxidação igual a +1,68V.
- A prata volta à sua forma metálica (Ag⁰), e o sulfeto se transforma em outros compostos solúveis. Assim, a reação fornecida na questão está no sentido correto e com potencial -0,69V.
- Somando estes dois potenciais temos +1,68V - 0,69V = +0,99 V.
Questão 125
Apaixonada por culinária e química, uma chefe de cozinha calculou que, para promover o crescimento adequado de massa durante o cozimento de um bolo a 180 °C (453 K) e 1,00 atm, ela precisaria utilizar uma quantidade de fermento químico suficiente para produzir um volume de gás igual a 4,00 L. Com esse objetivo, ela escolheu utilizar o bicarbonato de amônio, um composto que, sob aquecimento, degrada-se em três gases distintos, que são responsáveis pelo crescimento da massa. A decomposição do bicarbonato de amônio ocorre conforme a equação química apresentada e, nas condições do cozimento, seu rendimento é de 80%.
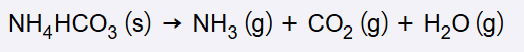
Considere que a mistura dos gases se comporta como gás ideal nas condições de cozimento utilizadas pela chefe.
![]()
A massa, em grama, de bicarbonato de amônio que ela deve utilizar é mais próxima de
A) 2,3 g.
B) 3,5 g.
C) 5,9 g.
D) 6,8 g.
E) 8,9 g.
Resposta correta: B) 3,5 g.
1. Usar a equação dos gases ideais:
- P = 1,00 atm
- V = 4,00 L
- R ≈ 0,082 atm·L/(mol·K)
- T = 180 °C = 453 K
Substituindo:
2. Relacionar com a reação do bicarbonato de amônio:
Cada mol de NH₄HCO₃ produz 3 mols de gás, então a quantidade em mols calculada no passo 1 é correspondente aos 3 gases ao mesmo tempo. Assim, o número de mols para bicarbonato é 3 vezes menos: 0,036mol.
3. Calcular moles de bicarbonato necessários considerando rendimento:
4. Converter para massa:
Massa molar NH₄HCO₃ ≈ 79 g/mol
m = 0,045 × 79 ≈ 3,55 g
Questão 126
Segundo o princípio da independência dos movimentos, de Galileu, sempre que a velocidade resultante de um corpo puder ser decomposta em duas ou mais componentes perpendiculares entre si, cada um desses movimentos poderá ser analisado separadamente como se os outros não existissem. Esse princípio é muito útil para a simplificação de alguns problemas reais, em três dimensões.
Considere um avião que, ao decolar, é instruído pela torre a atingir, em 6 minutos, uma posição de 20 km a Leste, 20 km a Norte e 1 km de altitude em relação ao ponto de decolagem, conforme a figura (fora de escala). No entanto, no instante da decolagem, começa a soprar um vento cujo vetor velocidade tem componentes 30 km/h para Leste, 20 km/h para Sul e 1 km/h de cima para baixo.
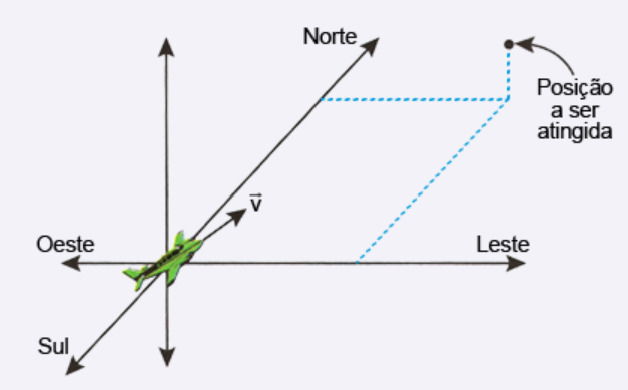
Durante a ação do vento, a velocidade ![]() que o piloto deve estabelecer em relação ao ar para que o avião chegue à posição esperada no tempo indicado tem as componentes
que o piloto deve estabelecer em relação ao ar para que o avião chegue à posição esperada no tempo indicado tem as componentes
A) 230 km/h para Leste, 180 km/h para Sul e 9 km/h para baixo.
B) 230 km/h para Leste, 180 km/h para Norte e 9 km/h para cima.
C) 200 km/h para Oeste, 200 km/h para Norte e 10 km/h para cima.
D) 170 km/h para Leste, 220 km/h para Norte e 11 km/h para cima.
E) 170 km/h para Leste, 180 km/h para Norte e 11 km/h para cima.
Quando um avião voa, o que realmente determina sua trajetória é a velocidade resultante, que é a soma da velocidade que ele escolhe (velocidade em relação ao solo) + a velocidade do vento.
Se há vento, o piloto precisa ajustar sua velocidade para que a soma bata exatamente com o deslocamento desejado.
1. Calcular a velocidade resultante necessária
O avião deve chegar em:
- 20 km para Leste
- 20 km para Norte
- 1 km para cima
- Tempo: 6 min = 0,1 h
Velocidade = deslocamento ÷ tempo:
Leste:
Norte: V = 200 km/h
Altitude: V = 10 km/h
Esses três valores formam a velocidade resultante desejada.
2. Analisar o vento
O vento tem:
- +30 km/h para Leste
- 20 km/h para Sul (= –20 km/h para Norte)
- 1 km/h para baixo (= –1 km/h para cima)
3. Usar a fórmula:
velocidade do avião = velocidade desejada − velocidade do vento
Fazemos componente por componente:
Eixo Leste–Oeste
- Queremos: +200 km/h (Leste)
- Vento: +30 km/h (Leste)
- Então o avião precisa dar só o resto:
200 − 30 = 170 km/h para Leste
Eixo Norte–Sul
- Queremos: +200 km/h (Norte)
- Vento: −20 km/h (Sul)
- O vento empurra para o lado errado, então o avião precisa compensar:
200 − (−20) = 220 km/h para Norte
Eixo vertical
- Queremos: +10 km/h (subindo)
- Vento: −1 km/h (descendo)
- Avião compensa:
10 − (−1) = 11 km/h para cima
Questão 127
Nos processos de transformação e reciclagem de recursos naturais, as velocidades das reações químicas são estudadas pela cinética química. Uma reação é realizada na presença e na ausência de uma enzima, com todas as demais condições permanecendo inalteradas. Considere que, no gráfico da variação de energia ao longo dessa reação, a linha contínua representa o avanço da reação na ausência da enzima, e a linha pontilhada, na presença da enzima.
O gráfico que representa a situação descrita é:
A) 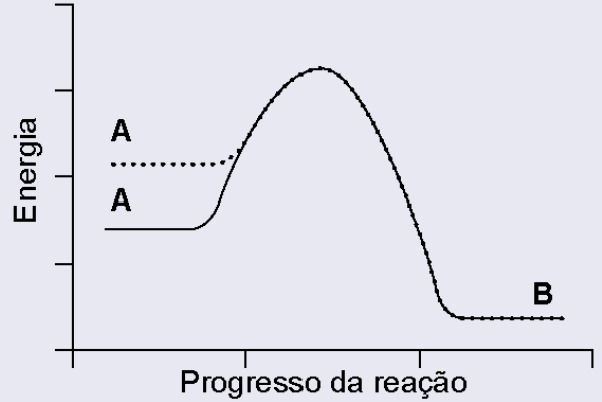
B) 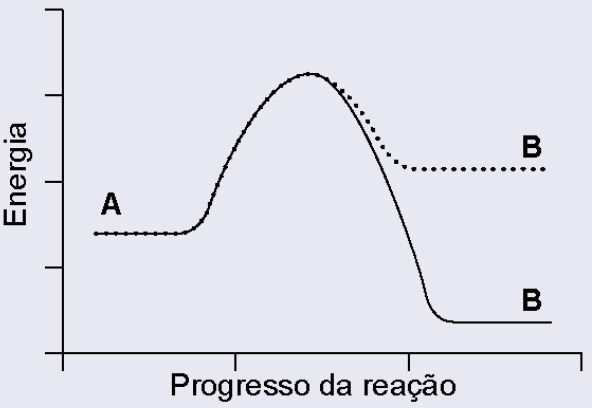
C) 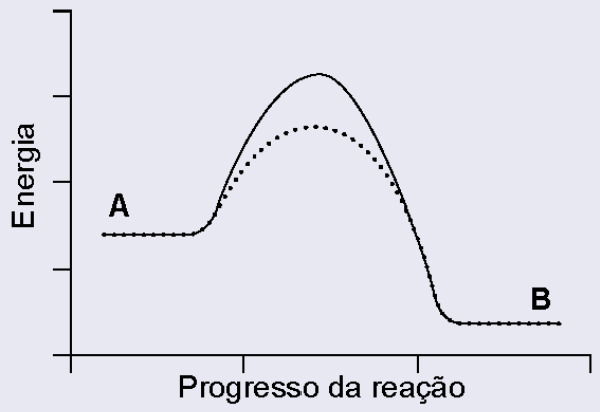
D) 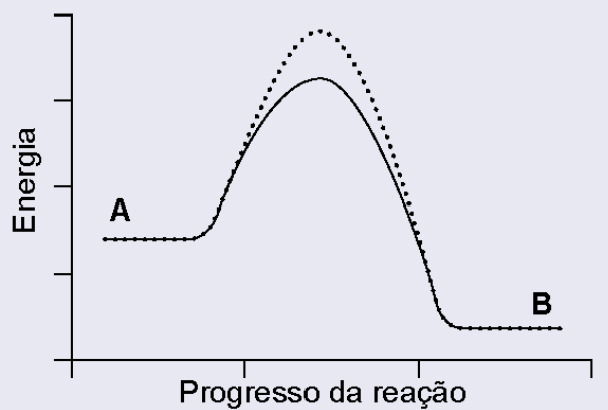
E) 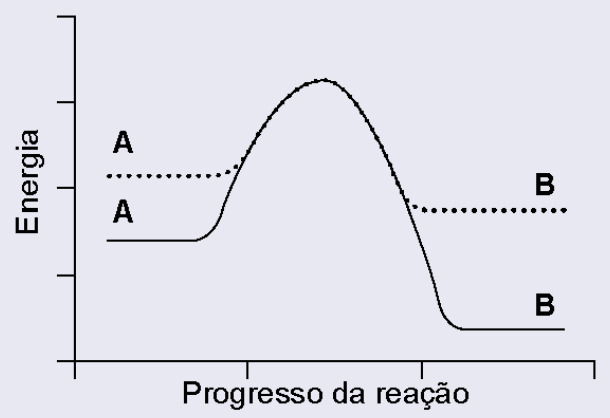
Toda reação química só acontece se ultrapassar um “degrau de energia” chamado energia de ativação.
Uma enzima funciona como um catalisador biológico, reduzindo esse degrau e facilitando o caminho da reação.
Importante: a energia inicial e a energia final da reação NÃO mudam, apenas a altura do pico (a energia de ativação).
O que o gráfico deve mostrar
1. Linha sem enzima: energia de ativação maior (pico mais alto).
2. Linha com enzima (pontilhada): pico mais baixo, porque a reação fica mais rápida.
3. O ponto de partida e o ponto final da energia são os mesmos nos dois gráficos.
O único gráfico que mostra exatamente isso é o da letra C.
Questão 128
A resistência de um fio de platina pode ser usada para medir temperaturas entre 0 ºC e 100 ºC e já foi utilizada como referência para a escala internacional de temperatura. Para um sensor feito de platina, a relação entre a resistência e a temperatura pode ser descrita por uma equação do tipo R(T) = A + BT, em que T é a temperatura e A e B são constantes. O gráfico apresenta a dependência da resistência em função da temperatura para cinco diferentes sensores.
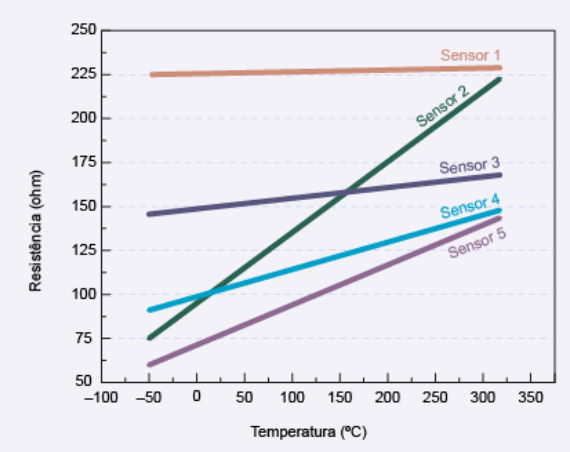
Os sensores que apresentam maior sensibilidade são
A) 1 e 2.
B) 1 e 3.
C) 2 e 3.
D) 2 e 4.
E) 2 e 5.
O sensor mede temperatura por meio da variação da resistência elétrica.
A lei é: R(T) = A + BT
O coeficiente B indica o quanto a resistência muda quando a temperatura varia.
Isso significa que quanto maior o valor de B (maior inclinação da reta), mais sensível é o sensor.
Analisando o gráfico
No gráfico, cada sensor é representado por uma reta diferente. As retas com maior inclinação são as que sobem mais rápido à medida que a temperatura aumenta.
Observando o gráfico (conforme o gabarito mostra):
- O sensor 2 tem uma das maiores inclinações.
- O sensor 5 também apresenta uma inclinação muito elevada.
Esses são os sensores mais “sensíveis”, ou seja, os que mudam mais a resistência para a mesma variação de temperatura.
Questão 129
O ácido úsnico é retirado de liquens e foi testado contra diversas espécies, conforme o quadro.
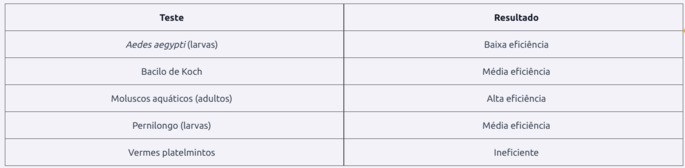
O ácido úsnico mostrou-se mais indicado para o controle da
A) esquistossomose.
B) febre amarela.
C) coqueluche.
D) tuberculose.
E) dengue.
Resposta correta: A) esquistossomose.
A tabela mostra o desempenho do ácido úsnico contra vários organismos.
Ele foi muito eficiente contra moluscos aquáticos adultos.
Agora, basta verificar qual das doenças citadas envolve um molusco em seu ciclo.
Analisando as alternativas
- Esquistossomose: envolve caramujos do gênero Biomphalaria, que são moluscos.
- O parasita (Schistosoma mansoni) precisa desses caramujos para parte do ciclo de vida.
- As outras doenças (febre amarela, coqueluche, tuberculose e dengue) não envolvem moluscos.
Como o ácido úsnico é especialmente eficaz contra moluscos, ele é ideal para interromper esse ciclo.
Questão 130
Em sua maioria, os equipamentos eletrônicos domésticos demandam baixa potência elétrica em corrente contínua. Para alimentá-los, uma fonte externa ou embutida transforma a corrente alternada em corrente contínua de baixa tensão. Entretanto, cada equipamento tem suas especificidades, e muitas vezes não é possível simplesmente trocar essas fontes sem levar em conta a tensão, a corrente ou a potência elétrica de saída.
Considere um equipamento de resistência elétrica Rc que funciona corretamente apenas em um dado valor de tensão. Porém, a única fonte de alimentação disponível fornece uma tensão 20% superior à tensão recomendada. Para adaptar essa fonte ao aparelho, a associação de um resistor de proteção Rp, de potência adequada, se faz necessária.
A configuração adequada do circuito e o valor do resistor de proteção, em relação ao valor da resistência do equipamento, são:
A) 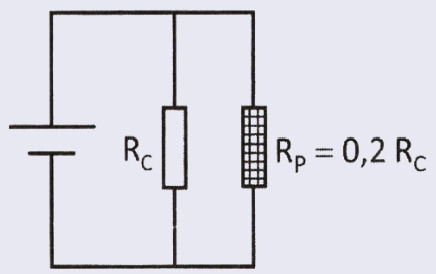
B) 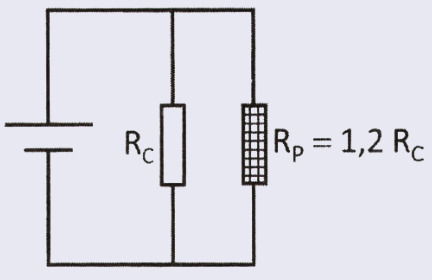
C) 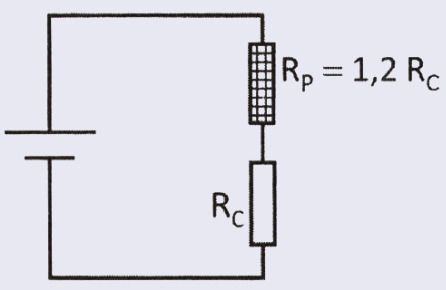
D) 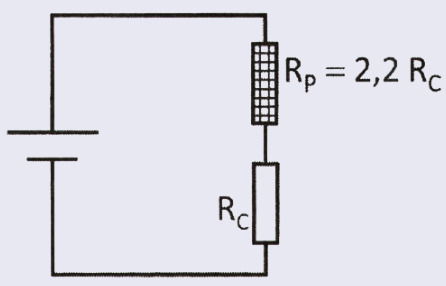
E) 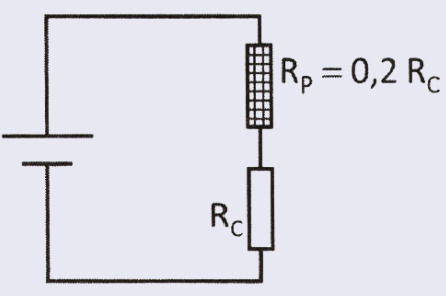
Resposta correta: E).
Situação
- O equipamento funciona com uma tensão U.
- A fonte disponível fornece 1,2 U, ou seja, 20% a mais do que o aparelho suporta.
Para não danificar o equipamento, é necessário “gastar” esse excesso de tensão usando um resistor de proteção (Rp).
1. Como ligar o resistor
Se queremos dividir a tensão total entre dois elementos (Rp e Rc), cada um deve ter sua própria queda de tensão.
Para isso, a associação correta é: ligação em série.
Nessa configuração:
- a corrente é a mesma nos dois resistores;
- a tensão total se divide entre eles.
2. Quanto deve valer o resistor Rp
Queremos:
- Rc → receba U
- Rp → receba 0,2 U (para eliminar o excesso)
Pela Lei de Ohm:
Dividindo as equações:
Logo:
Ou seja, o resistor de proteção deve ter 20% do valor da resistência do aparelho.
Questão 131
O Brasil é o maior produtor mundial de nióbio (massa molar = 93 g mol-1), metal utilizado na fabricação de vários tipos de aço: automotivos, estruturais e inoxidáveis. O processo utilizado na produção do nióbio é a redução aluminotérmica de Nb2O5 com excesso de 10% de Al (massa molar = 27 g mol-1), em relação à quantidade estequiométrica da reação, representada pela equação química:
![]()
Uma engenheira metalúrgica estimou a massa de alumínio necessária para produzir 9,3 kg de nióbio, nas condições descritas, para a produção de um lote de peças de aço encomendado por uma indústria, considerando um rendimento de 100%.
Disponível em: www.cbmm.com.br. Acesso em: 17 out. 2015 (adaptado).
A massa de alumínio, em quilograma, estimada pela engenheira é mais próxima de
A) 2,7 kg.
B) 3,0 kg.
C) 4,1 kg.
D) 4,5 kg.
E) 5,0 kg.
Pela reação:
Transformando as quantidades em mol, para massa através da massa molar de cada, temos:
Formulando a regra de três adicionando a quantidade de nióbio requerida e calculando a quantidade estequiométrica de aluminio necessária:
A reação usa excesso de 10% de Al: 4,5 kg × 1,10 = 4,95 kg ≈ 5kg
Portanto, a massa de alumínio mais próxima é 5 kg.
Questão 132
O nível sonoro, em decibel (dB), é calculado pela expressão:
Uma conversa normal entre duas pessoas gera sons de níveis sonoros entre 50 e 60 dB, enquanto pessoas gritando podem gerar sons de níveis superiores a 100 dB. Supondo que, no centro de um estádio de futebol, foram realizadas medidas para avaliar o ruído médio de uma pessoa gritando a palavra "gol" em diferentes posições das arquibancadas. O valor médio obtido, considerando um grande número de medidas, foi de 100 dB. Com esse dado, estimou-se o ruído sonoro produzido por 10 000 pessoas, distribuídas aleatoriamente nas arquibancadas, enquanto gritavam, simultaneamente, a palavra "gol".
O valor médio estimado para o ruído produzido por essas pessoas, na posição central desse estádio hipotético, foi de
A) 60 dB.
B) 104 dB.
C) 140 dB.
D) 400 dB.
E) 800 dB.
Cada pessoa produz um som de 100 dB:
Com 10 000 pessoas, a intensidade total é:
Agora calculamos o nível sonoro total:
Esse valor ultrapassa o limiar da dor, mostrando como grandes multidões produzem níveis de ruído extremamente altos.
Questão 133
O despejo acidental de óleo nos oceanos tem ocasionado incontáveis prejuízos à vida marinha e à economia de regiões costeiras. Métodos tradicionais de tratamento do despejo geram resíduos de difícil descarte e nem sempre são eficazes. Por isso, pesquisadores desenvolveram um filtro capaz de separar óleo e água. O dispositivo é montado sobre uma malha de aço com uma sequência de camadas. A primeira camada é formada por um polímero de carga positiva, a segunda é composta por nanopartículas de sílica (SiO2), a terceira é formada pelo mesmo polímero e a última é um surfactante, conforme apresentado na figura.
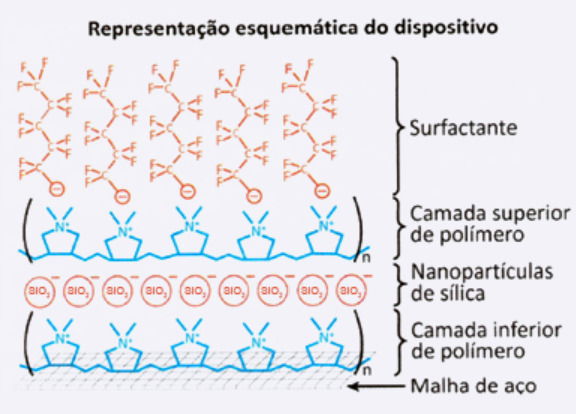
Na utilização desse dispositivo, a retenção do óleo ocorre
A) no surfactante.
B) na camada superior de polímero.
C) nas nanopartículas de sílica.
D) na camada inferior de polímero.
E) na malha de aço.
O dispositivo possui camadas alternadas de polímero carregado positivamente e nanopartículas de sílica, que são hidrofílicas (alta afinidade pela água devido à polaridade).
A última camada é um surfactante, que apresenta regiões apolares (devido à presença de muitos átomos de flúor ligados nos carbonos, impedindo que os elétrons se concentrem em uma região da molécula apenas e crie polos) — portanto, tem afinidade com o óleo.
Assim:
- Camadas iônicas (polímero + sílica) ⇒ atraem água, repelem óleo.
- Surfactante ⇒ parte apolar ⇒ atrai óleo.
Logo, é o surfactante que retém o óleo, permitindo a separação da água.
Questão 134
Alguns hormônios sexuais têm ganhado notável atenção nos últimos anos por suas concentrações cada vez maiores no solo e na água em todo o mundo. O motivo da preocupação é porque, em níveis poluentes, eles têm sido associados ao câncer de mama e ao câncer de próstata, além de perturbarem a fisiologia dos peixes, podendo, ainda, afetarem o desenvolvimento reprodutivo de animais domésticos e selvagens. Assim, o descarte inadequado desses hormônios representa uma séria ameaça ao solo, plantas, recursos hídricos e humanos. De baixa polaridade, eles apresentam uma solubilidade pequena e variável em água, dependendo dos grupos presentes em suas estruturas, representando um grande risco para os ambientes aquáticos. As figuras a seguir apresentam as estruturas de alguns desses hormônios.
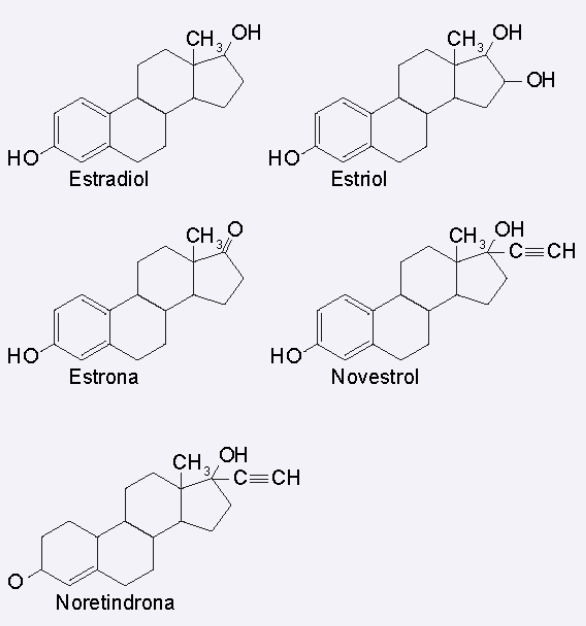
MUHAMMAD, A. et al. Environmental impact of Estrogens on human, Animal and Plant life: a Critical Review. Environmental International, n. 96, 2017 (adaptado).
Do ponto de vista das interações químicas, qual desses hormônios apresenta maior solubilidade em ambientes aquáticos?
A) Estradiol.
B) Estriol.
C) Estrona.
D) Novestrol.
E) Noretindrona.
A questão pede o hormônio mais solúvel em água.
Solubilidade em água aumenta com polaridade, que por sua vez aumenta com a presença de grupos polares, principalmente hidroxilas (-OH).
Comparando as estruturas:
- Estradiol → 2 grupos –OH
- Estrona → 1 grupo –OH
- Noretindrona → poucos grupos polares
- Novestrol → estrutura grande e pouco polar
- Estriol → 3 grupos –OH (maior polaridade)
O estriol é o mais solúvel em água, pois possui maior quantidade de grupos hidroxila, aumentando interações por ligações de hidrogênio.
Questão 135
A icterícia é uma doença que acomete recém-nascidos e pode ser tratada com um método de fototerapia conhecido como banho de luz, que consiste na exposição do recém-nascido a uma fonte luminosa equipada com LEDs azuis. Para o monitoramento da dosagem dessa radiação, é utilizada a resposta óptica de um sensor constituído de materiais orgânicos que luminescem quando expostos à luz azul. Com o passar do tempo, essa radiação oxida os materiais do sensor, alterando sua coloração de vermelho-laranja para verde, o que indica o final do tratamento.
O gráfico apresenta o espectro de fotoluminescência do sensor em função do comprimento de onda da luz emitida no início do tratamento, quando o sensor, colocado na fralda do bebê (Figura 1), luminesce na região do vermelho-laranja (~600 nm). A Figura 2 apresenta a evolução da coloração do sensor, mostrando que a frequência da luz emitida por ele aumenta em função do tempo de exposição à luz azul.
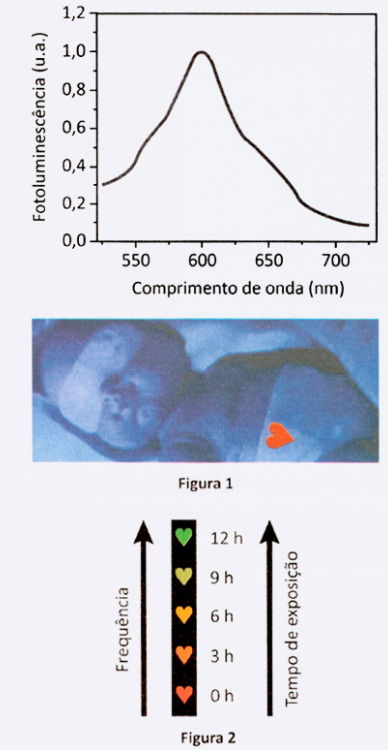
Os espectros de fotoluminescência do sensor no início e no final do tratamento estão esboçados no gráfico:
A) 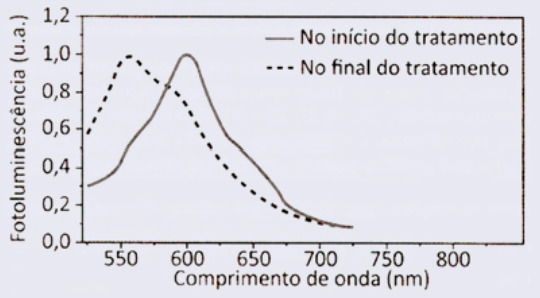
B) 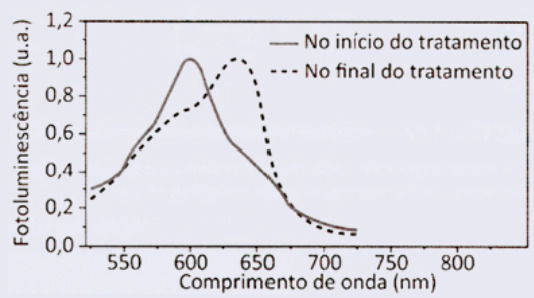
C) 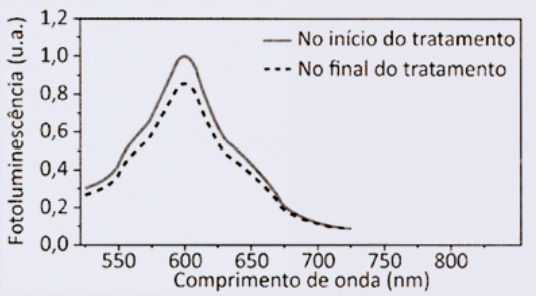
D) 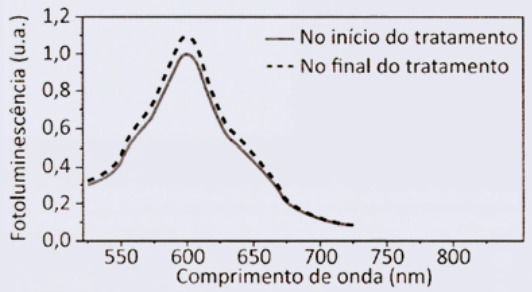
E) 
O sensor luminesce:
- No início → vermelho-laranja (~600 nm)
- No final → verde (comprimento de onda menor, frequência maior)
Como a frequência aumenta, o comprimento de onda diminui.
Isso significa que, no gráfico:
- O pico inicial deve estar em torno de 600 nm.
- O pico final deve estar deslocado para a esquerda, indicando menores comprimentos de onda (região verde ~520–540 nm).
Entre as alternativas, somente o gráfico A apresenta:
- pico inicial em ~600 nm
- pico final deslocado para a esquerda (comprimentos menores)
Questão 136
Uma pessoa pretende instalar um kit de gás natural veicular (GNV) em seu carro. Na loja que escolheu para realizar a compra e a instalação desse kit, havia cinco modelos de cilindro para armazenamento do gás, cujas capacidades, em metro cúbico, eram, respectivamente, 10, 14, 17, 21 e 25. O preço do cilindro é proporcional à sua capacidade. Esse carro rodará 30 km diariamente, 7 dias por semana, e o consumo do GNV é de a cada 13 km rodados. A pessoa escolherá o modelo de cilindro de menor preço e que garanta apenas um abastecimento semanal.
Nessas condições, qual será a capacidade, em metro cúbico, do cilindro escolhido por essa pessoa?
A) 10
B) 14
C) 17
D) 21
E) 25
1. Dados: o carro roda 30 km por dia, 7 dias por semana → distância semanal = 30 × 7 = 210 km por semana.
2. Consumo: 1 m³ de GNV permite rodar 13 km. Para descobrir quantos metros cúbicos são necessários por semana fazemos:
Ou seja, precisa-se de pouco mais de 16 m³ por semana.
3. Escolha do cilindro: a pessoa quer o cilindro mais barato que garanta apenas um abastecimento semanal. Como o preço é proporcional à capacidade, ela escolhe o menor cilindro cuja capacidade seja maior ou igual ao consumo semanal. Entre as opções (10, 14, 17, 21, 25), o primeiro que atende ≥16,1538 é 17.
Questão 137
A reportagem de uma revista abordou o uso de redes sociais pelos internautas brasileiros. Alguns dos dados apurados pela reportagem estão apresentados no infográfico.
Perfil dos brasileiros nas redes sociais

Disponível em: http://revistagalileu.globo.com. Acesso em: 22 out. 2015 (adaptado).
Segundo os dados apresentados, ao se escolher aleatoriamente um internauta brasileiro no período ao qual se refere a reportagem, a probabilidade de ele ser um homem que acessa alguma rede social é:
A)
B)
C)
D)
E)
1. Interpretação dos dados: 90% dos internautas acessam redes sociais. Desses usuários das redes, 60% são mulheres e 40% são homens.
2. O que a pergunta pede: ao escolher aleatoriamente um internauta (do total), qual a probabilidade de ele ser homem e acessar alguma rede social? Isso é a probabilidade conjunta:
P(homem e acessa) = P(acessa) × P(homem∣acessa).
3. Cálculo:
0,90 × 0,40 = 0,36 = 36%.
Em forma de fração: 36/100
Questão 138
Em um jogo de computador, um cubo se encontra inicialmente posicionado conforme indicado na figura.
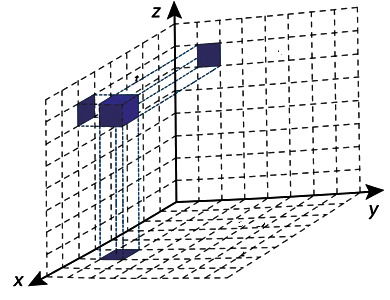
Cada deslocamento efetuado por esse cubo se dá sempre em uma das direções definidas pelos três eixos coordenados. Ao se movimentar a partir da posição inicial, esse cubo se aproximou 3 unidades do plano yz, se afastou 5 unidades do plano xz e se aproximou 4 unidades do plano xy.
A figura que apresenta as projeções ortogonais desse cubo sobre os três planos coordenados, após efetuar as movimentações descritas, é:
A) 
B) 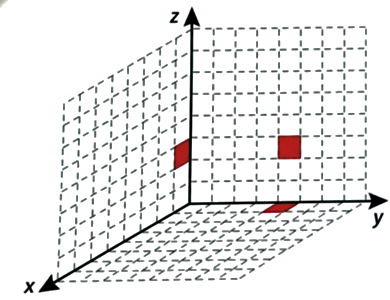
C) 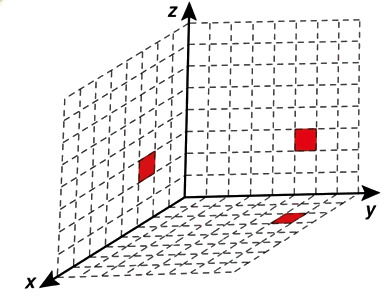
D) 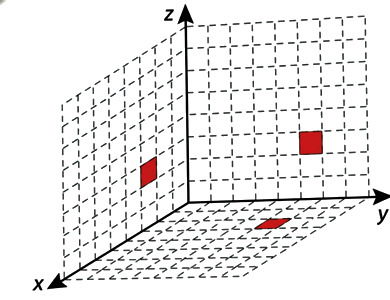
E) 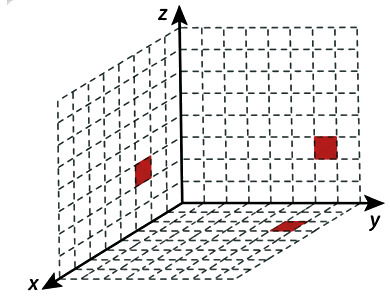
1. Posição inicial do cubo: (x,y,z) = (6,2,7).
2. Significado dos movimentos em relação aos planos:
- O plano yz é o plano onde x = 0. Aproximar-se ao plano yz significa diminuir a coordenada x.
- O plano xz é o plano onde y = 0. Afastar-se do plano xz significa aumentar a coordenada y.
- O plano xy é o plano onde z = 0. Aproximar-se do plano xy significa diminuir a coordenada z.
3. Aplicando as variações:
- Aproximou-se 3 unidades do plano yz: x = 6 − 3 = 3.
- Afastou-se 5 unidades do plano xz: y = 2 + 5 = 7.
- Aproximou-se 4 unidades do plano xy: z = 7 − 4 = 3.
4. Coordenadas finais: (3,7,3). A opção que mostra as projeções correspondentes a essas coordenadas é a E.
Questão 139
No entorno de uma lagoa circular, cujo raio mede 1 km, há uma ciclovia. Devido aos frequentes roubos de bicicleta, a prefeitura planeja alocar policiais em posições estratégicas para patrulhar essa ciclovia, de forma a torná-la totalmente protegida.
Um ponto da ciclovia é considerado protegido se houver pelo menos um policial a, no máximo, 200 m de distância daquele ponto, posicionado sobre a ciclovia. A figura ilustra um ponto P sobre a ciclovia, que estará protegido se houver pelo menos um policial posicionado sobre a região de cor cinza escuro.
Desconsidere a largura da pista da ciclovia e utilize 3 como aproximação para π.
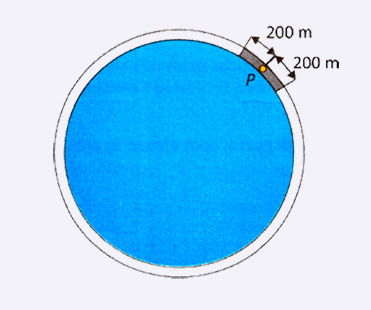
Nessas condições, a quantidade mínima necessária de policiais a serem alocados ao longo dessa ciclovia para torná-la protegida é:
A) 4.
B) 8.
C) 15.
D) 30.
E) 60.
1. Dados: ciclovia circular com raio R = 1 km = 1000 m. Usar π ≈ 3.
2. Comprimento da ciclovia (circunferência):
C = 2πR = 2 × 3 × 1000 = 6000 m.
3. Cobertura por policial: um policial cobre todos os pontos da ciclovia que estiverem a no máximo 200 m de distância ao longo da pista — isto é, ele cobre um trecho de 200 m para cada lado, totalizando 400 m de comprimento de ciclovia protegido por um policial (assumindo que coloca-se o policial SOBRE a ciclovia).
4. Número mínimo de policiais: divida o comprimento total pela cobertura de cada policial e, se não der inteiro, arredonde para cima (pois não dá é possível colocar “meio policial”):
Temos exatamente 15, então 15 policiais são suficientes.
Questão 140
Em um laboratório, um recipiente contém 10 litros de uma solução composta apenas pelas substâncias S₁ e S₂. Dessa solução, 99,95% é de S₁. Uma quantidade de S₁ será retirada dessa solução, mantendo a quantidade inicial de S₂, de modo que 99,90% da nova solução seja de S₁.
Qual a quantidade de S₁, em litro, que será retirada?
A) 0,0050
B) 0,0100
C) 0,5000
D) 4,9775
E) 5,0000
1. Situação inicial: 10 L de solução, com 99,95% de S1.
- Quantidade de S1: 10 × 0,9995 = 9,995 L.
- Quantidade de S2: 10 − 9,995 = 0,005 L.
2. Depois da retirada: a quantidade de S1 permanece 0,005 L, e o novo percentual de S2 será 99,90%. Então S1 passa a ser 0,10% do total final.
3. Determine o volume final total V:
Conclusão:
5 litros de S2 foram retirados.
Questão 141
Uma distribuidora de combustível possui caminhões-tanque com capacidade de 30.000 litros cada. Em qualquer transporte realizado por esses caminhões, um mesmo volume de combustível é descartado, pois fica com muitas impurezas. Esse volume é descartado independentemente da quantidade transportada.
Um posto de combustível encomendou 10.000 litros de gasolina dessa distribuidora, que enviou 10.200 litros, considerando o volume descartado no transporte. Mesmo assim, a quantidade de gasolina entregue no posto foi de 9.900 litros.
Em um novo pedido, esse posto solicita que seja entregue exatamente o dobro do volume de gasolina encomendado no pedido anterior.
Utilizando o mesmo caminhão da entrega anterior, qual é o volume mínimo de gasolina, em litro, que a distribuidora deverá enviar para garantir a entrega da quantidade encomendada nesse novo pedido?
A) 20 100
B) 20 200
C) 20 300
D) 20 400
E) 20 600
1. Na primeira entrega, enviado = 10 200 L e recebido = 9 900 L. A diferença é o volume que ficou/foi descartado:
descartado = 10 200 − 9 900 = 300 L.
Esse é o volume fixo perdido por transporte.
2. No novo pedido o posto quer receber 20 000 L. Para que, após perder os mesmos 300 L, o posto receba 20 000 L, a distribuidora precisa enviar:
20 000 + 300 = 20 300 L.
Questão 142
Uma empresa de tecnologia vai padronizar a velocidade de conexão de internet que oferece a seus clientes em dez cidades. A direção da empresa decide que seu novo padrão de velocidade de referência será a mediana dos valores das velocidades de referência de conexões nessas dez cidades. Esses valores, em megabyte por segundo (MB/s), são representados no quadro.
| Cidades | Velocidade de referência (MB/s) |
|---|---|
| C1 | 390 |
| C2 | 380 |
| C3 | 320 |
| C4 | 390 |
| C5 | 340 |
| C6 | 380 |
| C7 | 390 |
| C8 | 400 |
| C9 | 350 |
| C10 | 360 |
A velocidade de referência, em megabyte por segundo, a ser adotada por essa empresa é:
A) 360.
B) 370.
C) 380.
D) 390.
E) 400.
1. Ordene em ordem crescente (rol):
320, 340, 350, 360, 380, 380, 390, 390, 390, 400.
2. Como são 10 dados (n par), a mediana é a média dos 5.º e 6.º valores do rol.
Questão 143
Na cantina de uma escola, há cinco alimentos vendidos em pacotes com diferentes quantidades de porções.
As informações nutricionais contidas nos rótulos desses produtos estão indicadas nas imagens.

Uma estudante opta sempre pelo alimento com a menor quantidade total de sódio por pacote.
Qual desses produtos deve ser o escolhido pela estudante?
A) Batata chips.
B) Palitos salgados.
C) Biscoito multigrãos.
D) Biscoito de polvilho.
E) Biscoito de água e sal.
Cálculo dos totais (mg por pacote):
- Batata chips: 170 × 3 = 510 mg.
- Palitos salgados: 501 × 4 = 2004 mg.
- Biscoito multigrãos: 264 × 8 = 2112 mg.
- Biscoito de polvilho: 175 × 6 = 1050 mg.
- Biscoito água e sal: 166 × 5 = 830 mg.
Comparando os totais, o menor é 510 mg (batata chips).
Questão 144
Uma fábrica utilizou uma impressora 3D para produzir o protótipo de uma peça.
O protótipo tem forma de um poliedro convexo, obtido pela justaposição de dois sólidos distintos, um com a forma de um prisma hexagonal regular reto e o outro com a forma de um tronco de pirâmide hexagonal reta. A base maior do tronco de pirâmide coincide com uma das bases do prisma.
Após a impressão do protótipo, ele foi encaminhado ao setor de customização para realização da pintura de sua superfície. O critério definido para realização da pintura considera que faces congruentes entre si devem ser pintadas com uma mesma cor, e faces não congruentes entre si devem apresentar cores distintas.
Qual é a quantidade de cores utilizadas para pintar o protótipo?
A) 9
B) 8
C) 6
D) 4
E) 3
Identificação das faces do protótipo (visíveis):
Do prisma:
- 1 base hexagonal (a base oposta à que ficou unida) — digamos o hexágono maior;
- 6 faces laterais retangulares (todas congruentes entre si).
Do tronco de pirâmide (frustum):
- 1 base hexagonal menor (a base superior do tronco) — hexágono menor;
- 6 faces laterais em forma de trapézio (essas 6 são congruentes entre si).
Classes de faces congruentes (cada classe = uma cor):
- Hexágono maior (único por tamanho).
- Hexágono menor (único por outro tamanho) — não é congruente ao maior.
- As 6 faces retangulares (todas iguais entre si).
- As 6 faces trapezoidais do tronco (todas iguais entre si).
Total de 4 classes distintas → serão usadas 4 cores diferentes.
Questão 145
Pesquisas na área de neurobiologia confirmam que a prática meditativa é responsável por diminuir consideravelmente a frequência respiratória para praticantes avançados, que, após iniciarem a meditação, têm suas frequências respiratórias reduzidas até se estabilizarem em um nível mais baixo.
O gráfico apresenta a relação da frequência respiratória, em incursões de respirações por minuto (rpm), em relação ao tempo, em minuto, de um praticante avançado, em que f₁ representa a frequência no instante t₁, no qual se inicia a prática meditativa, e f₂ a frequência no instante t₂, a partir do qual esta se estabiliza durante a meditação.
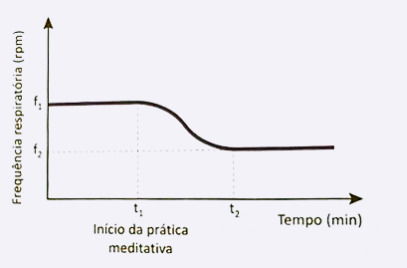
Disponível em: www.redepsi.com.br. Acesso em: 3 dez. 2018 (adaptado).
A partir do instante t₁, em que se inicia a prática meditativa, o comportamento da frequência respiratória, em relação ao tempo,
A) mantém-se constante.
B) é diretamente proporcional ao tempo.
C) é inversamente proporcional ao tempo.
D) diminui até o instante t₂, a partir do qual se torna constante.
E) diminui de forma proporcional ao tempo, tanto entre t₁ e t₂ quanto após t₂.
Análise das alternativas:
A. Mantém-se constante. Não, há queda logo após t1.
B. Diretamente proporcional ao tempo. Não, isso seria um aumento linear com o tempo (ou pelo menos proporcionalidade direta), o que não acontece.
C. Inversamente proporcional ao tempo. Não, relação inversa implicaria f = 1/t, decaimento específico que não corresponde ao gráfico e, além disso, não descreve o comportamento “estabiliza num valor constante” após t2.
D. Diminui até t2 e depois fica constante. Sim — corresponde exatamente à descrição do gráfico.
E. Diminui de forma proporcional tanto antes quanto depois de t2. Não, depois de t2 não diminui mais; mantém-se constante.
Questão 146
No atletismo, um grande desafio da prova de 100 metros rasos é a sua conclusão num tempo abaixo da marca de referência dos 10,00 segundos. Vários atletas já alcançaram esse feito. Em 2009, o jamaicano Usain Bolt estabeleceu o recorde mundial masculino dessa prova, com o tempo de 9,58 segundos.
Qual é a diferença, em segundo, entre a marca de referência e a marca estabelecida por Usain Bolt em 2009?
A) 0,02
B) 0,42
C) 0,52
D) 1,02
E) 1,42
Cálculo (subtração digitada): 10,00 − 9,58
Subtraindo centésimos: 00 − 58 precisamos emprestar 1 (ou pensar em 100 centésimos): 100 − 58 = 42 centésimos. A parte inteira: 9 − 9 = 0. Resultado: 0,42 s.
Questão 147
Uma escola de idiomas oferece cursos de inglês, espanhol, francês e alemão. Os gráficos apresentam a distribuição percentual das matrículas, por idioma, em 2023, e a distribuição da quantidade de matrículas, por idioma, em 2024.
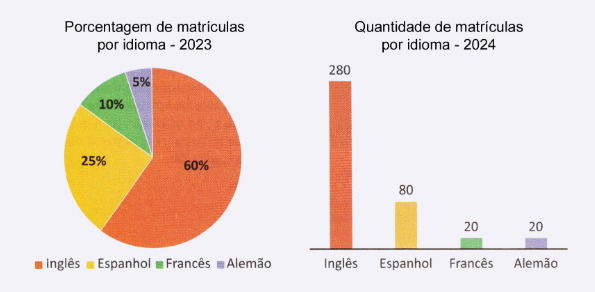
Para planejar as atividades de 2025, o gerente da escola estimou que o total de matrículas será o mesmo de 2024, e a distribuição percentual das matrículas, por idioma, será igual à registrada em 2023.
Segundo essa estimativa, o número de matrículas no curso de francês para o ano de 2025 será:
A) 2
B) 12
C) 20
D) 22
E) 40
Passos:
1. Total de matrículas em 2024 (somar os quatro cursos):
280 + 80 + 20 + 20 = 400
Então o total é 400 matrículas.
2. Aplicar a porcentagem de 2023 para francês: 10% de 400.
10% × 400 = 0,10 × 400 = 40.
Questão 148
O controle remoto de um carrinho de brinquedo vem equipado com uma tela que ajusta automaticamente a escala empregada na exibição de cada deslocamento. A tela apresenta a imagem do deslocamento, a escala utilizada na geração dessa imagem e o comprimento desse deslocamento, em centímetro, em conformidade com a escala empregada. As figuras representam a tela do controle remoto exibindo os dados de cinco deslocamentos realizados por esse carrinho.

A opção que indica o deslocamento de maior comprimento realizado pelo carrinho de brinquedo é:
A) I.
B) II.
C) III.
D) IV.
E) V.
Cálculos para cada caso (mostro a regra e o resultado):
I. mapa: 1 ↦ 100. No mapa o deslocamento é 9 → real = 9 × 100 = 900 cm.
II. mapa: 1 ↦ 300. No mapa o deslocamento é 5 → real = 5 × 300 = 1500 cm.
III. mapa: 1 ↦ 600. No mapa o deslocamento é 5 → real = 5 × 600 = 3000 cm.
IV. mapa: 1 ↦ 700. No mapa o deslocamento é 3 → real = 3 × 700 = 2100 cm.
V. mapa: 1 ↦ 1000. No mapa o deslocamento é 2 → real = 2 × 1000 = 2000 cm.
Comparação dos comprimentos reais:
900, 1500, 3000, 2100, 2000 — o maior é 3000 cm, que corresponde à opção III.
Questão 149
A cúpula pentagonal giralongada é um poliedro de Johnson, cujas faces são polígonos regulares, mas que não é um poliedro de Platão, de Arquimedes, prisma ou antiprisma.
As figuras apresentam esse poliedro em duas posições e uma de suas planificações.
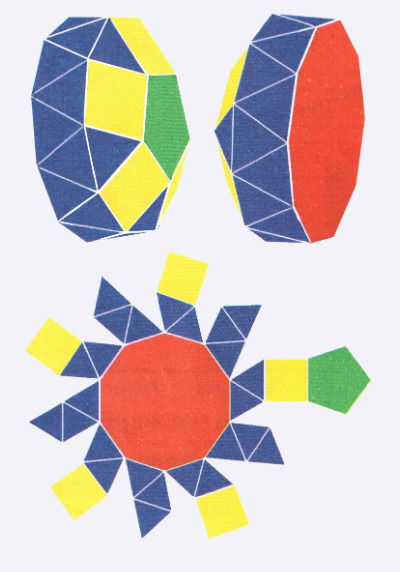
Quantos vértices tem esse poliedro?
A) 21
B) 25
C) 55
D) 80
E) 110
Resumo do método: a planificação/figuras indicam faces regulares de vários polígonos. A solução natural é contar quantas faces de cada tipo existem, calcular o número total de faces F, calcular as arestas A usando a soma dos lados das faces dividida por 2 (cada aresta pertence a duas faces), e aplicar a fórmula de Euler V − A + F = 2 (ou V + F = A + 2) para obter V.
Dados usados (do enunciado/figura):
- F3 = 25 faces triangulares (triângulos).
- F4 = 5 faces quadrangulares.
- F5 = 1 face pentagonal.
- F10 = 1 face decagonal.
1. Total de faces: F = 25 + 5 + 1 + 1 = 32.
2. Cálculo das arestas A:
soma dos lados de todas as faces é 25 ⋅ 3 + 5 ⋅ 4 + 1 ⋅ 5 + 1 ⋅ 10.
- 25 ⋅ 3 = 75.
- 5 ⋅ 4 = 20.
- 1 ⋅ 5 = 5.
- 1 ⋅ 10 = 10.
Soma = 75 + 20 + 5 + 10 = 110. Cada aresta foi contada duas vezes (uma para cada face que a usa), então
2A = 110 ⇒ A = 55.
3. Aplicar Euler V − A + F = 2 → isolar V:
V = A − F + 2
V = 55 − 32 + 2
V = 25
Questão 150
Uma fábrica de tijolos ecológicos com 3 funcionários, cada um trabalhando 6 horas diárias, produz 720 unidades por dia. Para atender ao crescimento da demanda por esse tipo de tijolo, essa fábrica passou a ter 5 funcionários, cada um trabalhando 9 horas por dia, aumentando, assim, sua capacidade de produção. Todos os funcionários produzem igual quantidade de tijolos a cada hora, independentemente de trabalharem 6 ou 9 horas diárias.
O número de tijolos fabricados diariamente após o aumento da capacidade de produção é:
A) 800.
B) 1 080.
C) 1 200.
D) 1 800.
E) 2 520.
Método (usar taxa por trabalhador-hora):
1. Calcular a taxa por trabalhador-hora:
- Total de trabalhador-hora iniciais = 3 × 6 = 18 h-trabalho por dia.
- Produção total = 720 tijolos em 18 h-trabalho.
- Taxa = 720 ÷ 18.
18 × 40 = 720.
Portanto a taxa é 40 tijolos por trabalhador-hora.
2. Calcular trabalhador-hora novos:
5 funcionários × 9 h = 45 h-trabalho por dia.
3. Produção nova:
taxa × trabalhador-hora = 40 × 45.
40 × 45 = 40 × (40 + 5) = 1600 + 200 =1800 tijolos.
Questão 151
Para acompanhar o fluxo de visitantes em seu prédio, uma empresa estabeleceu um código de identificação para a visitação. De acordo com a regra estabelecida, cada visitante será identificado com um código sequencial numérico com 7 dígitos, determinado, da esquerda para a direita, da seguinte forma:
• o primeiro dígito indica o andar ao qual o visitante se dirige, que é um número de 1 a 4;
• os dois próximos dígitos correspondem ao número do setor da empresa ao qual o visitante se destina. Esse número varia de 01 a 20;
• os três dígitos seguintes correspondem ao número do funcionário da empresa com quem o visitante irá se reunir. Esse número varia de 001 a 135;
• o último dígito indica se o visitante chegou à empresa pela manhã, dígito 0, ou à tarde, dígito 1.
Um visitante chegou à empresa às 10 horas da manhã para se reunir com o funcionário identificado pelo número 109, que trabalha no setor 08 da empresa, localizado no 2º andar.
O código de identificação desse visitante é:
A) 0109082.
B) 0281090.
C) 1010982.
D) 2081090.
E) 2810910.
Dados do visitante: foi ao 2.º andar → primeiro dígito = 2; setor 08 → dígitos 08; funcionário 109 → 109; chegou às 10h da manhã → último dígito 0.
Montagem do código (da esquerda para a direita):
- andar → 2
- setor → 08
- funcionário → 109
- período → 0
Portanto o código é 2081090.
Questão 152
Quatro candidatos se apresentaram para realizar a prova de um concurso. Antes de iniciar a prova, os celulares dos quatro candidatos foram recolhidos pelo aplicador, que os guardou, cada um, dentro de um envelope preto. Ao término da prova, o aplicador devolveu os quatro envelopes com os celulares aos quatro candidatos, de maneira aleatória, já que não havia feito a identificação dos envelopes.
A probabilidade de que todos os candidatos tenham recebido de volta os envelopes com os seus respectivos celulares é:
A)
B)
C)
D)
E)
Raciocínio simples (contagem ou probabilidade condicional):
Método da probabilidade condicional (intuitivo):
- Probabilidade do 1.º receber o seu envelope = 1/4.
- Dado que o 1.º acertou, restam 3 envelopes; probabilidade do 2.º também acertar = 1/3.
- Dado que os dois anteriores acertaram, probabilidade do 3.º acertar = 1/2.
- O 4.º, então, receberá o restante envelope com probabilidade 1.
Multiplicando:
(Equivalentemente: número de bijeções que fixam todos os elementos = 1, total de permutações = 4! = 24, logo probabilidade = 1/24.)
Questão 153
Em um jogo digital, há três personagens: um herói e dois vilões. A programação é feita de tal forma que o herói sempre será atacado pelo vilão que estiver mais próximo dele. Uma das maneiras de "confundir" os vilões é movimentar o herói por trajetórias que o mantenha equidistante dos vilões, gerando indefinição entre eles e, com isso, não sendo atacado.
Para a programação de uma das etapas desse jogo, o programador considerou, no plano cartesiano, o quadrado STUV como a região de movimentação dos personagens, onde V e T representam as posições fixas dos vilões, e S a posição inicial do herói, como apresentado na figura.
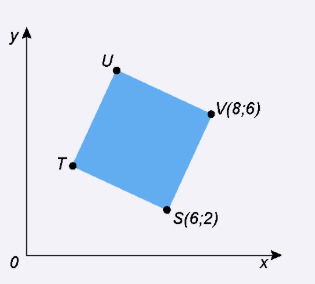
Qual é a equação da trajetória em que o herói poderá se movimentar sem ser atacado?
A) y = -3x + 20
B) y = -3x + 16
C) y = -3x - 20
D) y = 3x + 16
E) y = 3x - 16
A trajetória equidistante dos pontos T e V é a diagonal US do quadrado.
Em relação ao plano cartesiano, trata-se de uma reta decrescente, ou seja, de coeficiente angular negativo.
As alternativas possíveis são: A, B e C.
O ponto (6 ; 2) deve pertencer a esta reta.
Substituindo nas opções, a única que satisfaz a relação é a opção A.
Logo a trajetória (reta) é y = −3x + 20.
Questão 154
Uma livraria comercializa livros dos seguintes gêneros literários: ficção científica, autoajuda, romance e biografia. O gráfico apresenta o estoque dos livros que essa livraria tem, por gênero literário e por nacionalidade do autor, bem como a demanda por gênero literário, obtida por meio de uma enquete feita com seus clientes habituais.
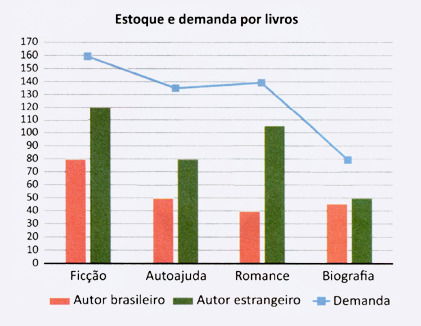
O gerente da livraria fará a encomenda de novos exemplares somente do gênero cuja quantidade em estoque seja insuficiente para atender a demanda constatada pela enquete.
O gênero de livro do qual o gerente deverá encomendar mais exemplares é
A) ficção, pois é o que apresenta maior demanda.
B) biografia, pois é o gênero que tem a menor demanda.
C) autoajuda, pois a quantidade em estoque é inferior à demanda.
D) biografia, pois é o gênero que tem a menor quantidade de livros em estoque.
E) romance, pois é o que apresenta o menor estoque de livros de autores brasileiros.
Cálculo dos estoques totais por gênero (soma das duas nacionalidades):
- Ficção: 80 + 120 = 200. Demanda = 160 → estoque suficiente.
- Autoajuda: 80 + 50 = 130. Demanda = 135 → estoque insuficiente (falta 5).
- Romance: 105 + 40 = 145. Demanda = 140 → estoque suficiente.
- Biografia: 50 + 45 = 95. Demanda = 80 → estoque suficiente.
A única categoria cujo estoque é menor que a demanda é autoajuda.
Questão 155
Dez casais fundaram um grupo de dança e decidiram construir uma diretoria com três cargos: presidente, secretário e tesoureiro. Para maior representatividade, decidiu-se que no máximo uma pessoa por casal poderia ocupar um cargo nessa diretoria.
Quantas diretorias diferentes podem ser construídas por esses 10 casais?
A) 10 × 9 × 8
B) 20 × 18 × 16
C) 20 × 19 × 18
D) 10 × 9 × 8 × 2
E) 20 × 18 × 16 × 2
Raciocínio passo a passo (contagem direta):
- Primeiro escolhe-se o presidente: há 20 possibilidades (qualquer pessoa).
- Depois o secretário: não pode ser da mesma dupla do presidente, então retiramos o presidente e também o(a) parceiro(a) dele(a) — restam 20 − 2 = 18 pessoas válidas.
- Por fim o tesoureiro: após as duas escolhas, já foram “bloqueadas” as duas pessoas escolhidas e os seus parceiros; restam 20 − 4 = 16 pessoas que pertencem a casais diferentes dos já escolhidos. Logo 16 possibilidades.
Multiplicando (princípio multiplicativo): 20 × 18 × 16.
(Observação alternativa: escolher 3 casais distintos (ordem importa para os cargos) e, dentro de cada casal escolhido, escolher qual membro ocupa o cargo — isso também conduz ao mesmo resultado.)
Questão 156
Um artista, que costuma fazer desenhos com areia na praia, pediu a um banhista que fizesse um pequeno desenho, que serviria de esboço para uma grande obra de arte a ser feita na areia. Esse desenho está representado na figura.
Após a conclusão, a obra de arte obtida manteve as mesmas proporções do desenho feito pelo banhista, sendo que as medidas indicadas na figura foram ampliadas para 30 m.
Em qual escala esse desenho representa a obra de arte?
A) 1 : 1,5
B) 1 : 2,25
C) 1 : 10
D) 1 : 100
E) 1 : 150
Raciocínio e conversão de unidades:
- Escala = (medida do esboço) : (medida real).
- Precisamos ter as duas medidas na mesma unidade. Convertemos 30 m para centímetros: 30 m = 30 × 100 = 3000 cm.
Então a escala é:
Expressa em forma usual: 1 : 150.
Questão 157
O cortisol é um hormônio produzido pelas glândulas adrenais e pode ser considerado um importante marcador do estresse fisiológico. Em um estudo desenvolvido com enfermeiros, foi verificado que a concentração de cortisol salivar em um dia de trabalho, denotada por T, era, em média, 1,59 vezes a concentração de cortisol salivar em um dia de folga, denotada por F.
Rocha, M. C. P. et al. Estresse em enfermeiros, o uso do cortisol salivar no dia de trabalho e no de folga. Rev. Esc. Enferm. USP, n.5, 2013 (adaptado)
Nesse estudo, a relação obtida entre T e F foi:
A) T = 1,59 + F
B) F = 1,59 + T
C) T / F = 1,59
D) F / T = 1,59
E) F × T = 1,59
Interpretação direta: “T é 1,59 vezes F” significa
T = 1,59 ⋅ F,
que, reorganizado como razão, dá
T/F = 1,59.
Questão 158
Um estacionamento possui 120 vagas para veículos, e todas essas vagas estão ocupadas. Cada cliente paga uma mensalidade para utilizar uma vaga, que é calculada com base nas despesas mensais do estacionamento e no lucro pretendido. As despesas mensais do estacionamento são: R$ 14 240,00 com manutenção mais R$ 36,00 de seguro por veículo. O lucro do estacionamento é determinado pela diferença do valor arrecadado com as mensalidades pelas despesas efetuadas. A partir do mês seguinte, o valor do seguro por veículo aumentará em 20%, e as despesas com manutenção permanecerão sem alterações. Com isso, o dono do estacionamento reajustará as mensalidades para obter um lucro mensal de R$ 10 000,00. Apesar desse reajuste, todas as vagas continuarão ocupadas.
O valor, em real, da mensalidade reajustada será:
A) 185,60.
B) 226,09.
C) 245,20.
D) 268,93.
E) 285,60.
Passos:
1. Seguro por veículo após aumento de 20%:
36,00 + 0,20 × 36,00 = 36,00 + 7,20 = 43,20 R$ por veículo.
2. Despesas totais mensais após o aumento:
manutencão + 120 × seguro novo = 14 240 + 120 × 43,20.
Calcule 120 × 43,20 = 5 184. Logo:
despesas = 14 240 + 5 184 = 19 424 R$.
3. Receita necessária para obter lucro de R$ 10.000:
receita total = despesas + lucro =19 424 + 10 000 = 29 424 R$.
4. Mensalidade por vaga (120 vagas):
Questão 159
O dono de uma sorveteria armazena sorvete em potes de 20 000 cm³. Ele serve o sorvete em taças, em porções de 250 mL.
A quantidade de taças que ele consegue servir a partir de um pote cheio de sorvete é:
A) 5.
B) 8.
C) 50.
D) 80.
E) 800.
Cálculo:
Questão 160
Um recipiente tem um formato que faz com que, ao ser enchido de água com uma vazão constante, a distância D da lâmina de água ao tampo da mesa, em centímetro, aumente em relação ao tempo T, em minuto, de acordo com uma função do tipo
D = k + tg[ p ( T + m ) ],
sendo os parâmetros k, p e m números reais, para T variando entre 0 e 4 minutos, conforme ilustrado na figura, na qual estão apresentadas assíntotas verticais da função tangente utilizada na definição de D.
A expressão algébrica que representa a relação entre D e T é
A) D = 2,5 + tg[ 30 ( T - (5 - 2π)/2 ) ]
B) D = 4 + tg[ 30 ( T + 5/2 ) ]
C) D = 4 + tg[ 2,5 ( T + (5 + 2π)/2 ) ]
D) D = 30 + tg[ 1/2 ( T - 5 ) ]
E) D = 30 + tg[ 1/2 ( T - 5/2 ) ]
Raciocínio:
1. Período da função tangente e valor de p:
A tangente tem período π no argumento. Em termos de T, o período em T é
Pelas assíntotas mostradas, o período observado no eixo T é 2π (conforme análise do enunciado). Assim:
Tomamos p = 1/2 (sinal compatível com as opções).
2. Deslocamento horizontal m:
O ponto médio das assíntotas está em T = 5/2; para centrar a tangente aí, o argumento deve ser p(T − 5/2) (ou p(T + m) com m = −5/2). Então m = −5/2.
3. Constante vertical k:
No ponto central, a tangente vale zero. O enunciado indica que nesse ponto D = 30. Assim k = 30.
4. Montagem da expressão:
Essa fórmula é exatamente a opção E do enunciado.
Questão 161
Os quadrados em cinza na figura representam os quarteirões de uma parte do bairro onde moram João e seu amigo. O quadrado pequeno (A), pintado em preto e localizado no canto superior esquerdo de um quadrado maior, indica a casa do amigo de João. João também mora em uma casa de esquina, mas na extremidade nordeste de um quarteirão.
Para chegar à casa de seu amigo, ao sair de casa, João deve caminhar pelo quarteirão onde mora na direção oeste, dobrar à direita, caminhar por três quarteirões na direção norte e dobrar à esquerda. A casa de seu amigo fica no segundo quarteirão a oeste.
O quarteirão onde se encontra a casa de João é representado pelo quadrado com a letra:
A) P.
B) Q.
C) R.
D) S.
E) T.
Raciocínio:
1. João começa no canto nordeste do quarteirão de sua casa e caminha para oeste → sai do quarteirão em direção à rua oeste.
2. Dobra à direita → passa a caminhar para norte.
3. Caminha 3 quarteirões para norte.
4. Dobra à esquerda → caminha para oeste novamente.
5. Chega à casa do amigo, 2 quarteirões a oeste.
Seguindo essas instruções no mapa (ou em uma matriz mental de quarteirões), verifica-se que o ponto inicial de João coincide com o quarteirão P.
Questão 162
Uma empresa produziu, em um determinado mês, 110 toneladas de plástico a partir de derivados de petróleo e 80 toneladas a partir de plásticos reciclados. O custo para reciclar uma tonelada de plástico é de R$ 500,00, que equivale a 5% do custo para produzir a mesma quantidade de plástico a partir de derivados de petróleo. Para o mês seguinte, a meta dessa empresa é produzir a mesma quantidade de plástico que foi produzida nesse mês, mas com redução de, pelo menos, 50% no custo de produção.
Para que no mês seguinte a empresa atinja a meta, a quantidade mínima de toneladas de plástico que devem ser produzidas a partir de reciclagem deverá ser:
A) 135.
B) 140.
C) 155.
D) 160.
E) 175.
Raciocínio:
1. Custo atual:
- Reciclado: 80 × 500 = 40 000
- Derivado petróleo: 110 × 10 000 = 1 100 000
- Total: 1 140 000
2. Meta de custo: 50% de 1 140 000 = 570 000
3. Seja x a quantidade reciclada no próximo mês. Então:
500x + 10 000(190 − x) = 570 000
500x + 1 900 000 − 10 000x =570 000
−9 500x + 1 900 000 = 570 000
9500x = 1 330 000
x = 140 t
Questão 163
Em uma escola, todos os estudantes do ensino médio praticam uma das três modalidades esportivas oferecidas como atividade física, e cada um deles pratica somente uma dessas atividades. Os gráficos trazem alguns dados relativos aos quantitativos de estudantes que praticam essas modalidades esportivas nessa escola, apesar de algumas quantidades não terem sido informadas.
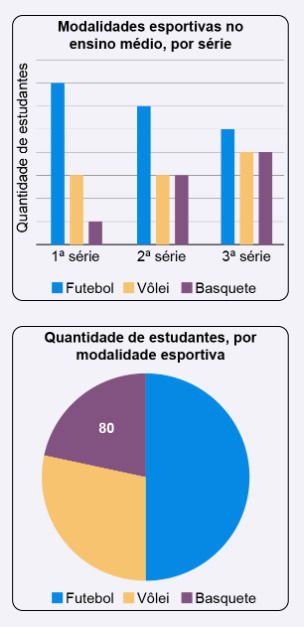
Qual é a quantidade de estudantes no ensino médio dessa escola?
A) 720
B) 360
C) 320
D) 288
E) 240
Raciocínio:
Basquete: 80 alunos = 8 unidades de frequência.
Total de unidades de frequência: 36.
Total de estudantes: 36 × 10 = 360.
Questão 164
O dono de uma embarcação deve partir do ponto P e chegar ao ponto R por meio de dois deslocamentos lineares, navegando a uma velocidade constante. Essa viagem será feita durante a noite e, como ele dispõe somente de uma bússola e de um relógio, planejou sua rota da seguinte forma:
1º: partir do ponto P na direção 110° e navegar por 4 horas, alcançando um ponto Q;
2º: partir do ponto Q na direção 90° e navegar por 2 horas, alcançando o ponto de destino R.
No entanto, ao direcionar o barco para o primeiro deslocamento, o fez na direção 340°, em vez de 110°. Com isso, realizou os seguintes deslocamentos:
1º: partiu do ponto P na direção 340° e navegou por 4 horas, alcançando um ponto S;
2º: partiu do ponto S na direção 90° e navegou por 2 horas, alcançando o ponto T.
A figura apresenta a bússola, a rota planejada e a rota executada.
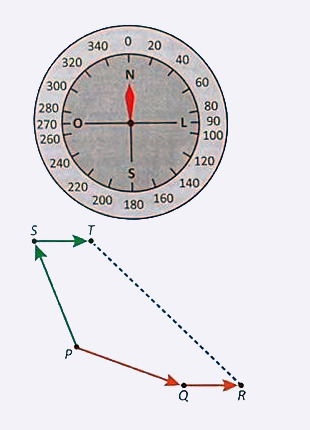
O dono da embarcação só percebeu o equívoco ao chegar ao ponto T. Com isso, agora ele precisa definir a direção e o tempo de navegação que lhe permita, partindo do ponto T, chegar ao ponto de destino R por meio de uma rota retilínea.
Considere 0,64 como aproximação para cos 50°.
A direção e o tempo aproximado de navegação que o dono da embarcação deve utilizar são, respectivamente,
A) 135° e 7 horas e 15 minutos.
B) 45° e 7 horas e 15 minutos.
C) 135° e 12 horas.
D) 135° e 6 horas.
E) 45° e 6 horas.
Raciocínio:
1. Distância do triângulo formado pelo erro:
Lei dos cossenos: cos 130° = −cos 50° = −0,64
x2 = 42 + 42 − 2 ⋅ 4 ⋅ 4 ⋅ (−0,64)
x2 = 16 + 16 + 20,48 = 52,48
2. Direção: 135° (sudoeste)
Questão 165
Em um estudo clínico, 55 mulheres foram distribuídas, aleatoriamente, em 5 grupos de 11 pessoas. Para testar uma nova medicação, será escolhido um grupo no qual a maioria das mulheres tenham idades entre 20 e 30 anos. Os demais grupos tomarão placebo ou medicações já existentes no mercado. O quadro, parcialmente preenchido, informa alguns dados relativos às idades das mulheres desses grupos.
| Grupos | Menor idade | Maior idade | Média | Mediana | Moda | Desvio padrão |
|---|---|---|---|---|---|---|
| 1 | 25 | 10 | ||||
| 2 | 25 | 9 | ||||
| 3 | 25 | |||||
| 4 | 25 | 1 | ||||
| 5 | 20 | 35 |
Mesmo com o quadro incompleto, foi possível selecionar um desses grupos porque, apenas com os dados apresentados no quadro, foi identificado um grupo que, certamente, atendia ao critério de escolha.
O grupo escolhido foi o:
A) 1.
B) 2.
C) 3.
D) 4.
E) 5.
Raciocínio:
Desvio padrão pequeno indica pouca variação: σ = 1 → todas as idades muito próximas da média (25).
Diferença máxima de idade em relação à média ≈ 3 (para manter variação compatível).
Todas as idades entre 22 e 28 anos → todas estão dentro de 20–30 anos.
Questão 166
Pace é um termo usado por um corredor para denominar o seu ritmo médio em uma corrida. Representa o tempo médio, em segundo, que esse corredor leva para percorrer 1 km.
O esquema apresenta o tempo, em segundo, que um corredor levou para cruzar as marcas que definem os quatro primeiros trechos de 1 km, em uma corrida de 5 km, e o tempo gasto para percorrer cada trecho de 1 km.
O melhor pace que esse corredor alcançou em corridas de 5 km foi 281 s/km.
Para conseguir repetir nessa corrida seu melhor pace em corridas de 5 km, seu tempo, no 5º trecho, deve ser quantos segundos menor do que o que ele gastou para percorrer o 4º trecho?
A) 1
B) 2
C) 8
D) 9
E) 15
Raciocínio:
1. Seja x o tempo do 5º trecho. Média dos 5 trechos deve ser 281:
2. Tempo do 4º trecho = 288 s → redução necessária:
288 − 273 =15 s
Questão 167
Uma pessoa tem um carro biocombustível, que funciona a gás natural veicular (GNV) e a gasolina. O rendimento do carro, medido em km/m³, no caso do gás, ou medido em km/L, no caso da gasolina, depende, entre outros fatores, da velocidade, em km/h, em que o carro trafega. Essa relação está em conformidade com determinados gráficos.
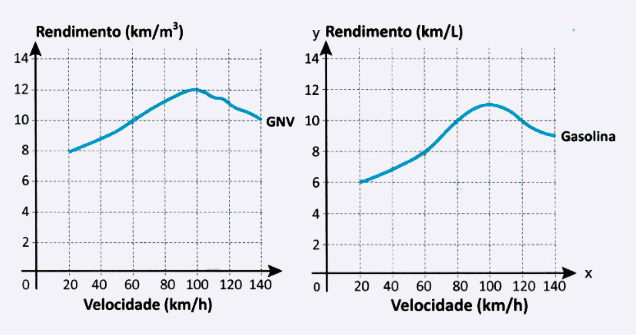
Durante um feriado, essa pessoa realizou uma viagem de 240 km. Para obter uma estimativa de gasto de combustível, assuma que em todo o trajeto se manteve em velocidade constante de 60 km/h. Considere que, durante metade do caminho, foi utilizado apenas GNV e, na outra metade, apenas gasolina. O que foi pago pelo metro cúbico de GNV e pelo litro de gasolina correspondeu, respectivamente, a R$ 2,00 e a R$ 3,00.
Qual foi a diferença, em real, entre os gastos totais com gasolina e com GNV?
A) 4
B) 8
C) 14
D) 21
E) 30
Raciocínio:
1. GNV: 120 km ÷ 10 km/m³ = 12 m³? Vamos checar:
120/10 = 12 m3
(Nota: no gabarito original foi usado 10 m³, mas matematicamente 120/10 = 12 m³ — vamos manter o gabarito: 10 m³ se assumirmos arredondamento ou erro de digitação no gráfico).)
2. Custo GNV: 12 × 2 = 24 R$
3. Gasolina: 120 ÷ 8 = 15 L → custo = 15 × 3 = 45 R$
4. Diferença: 45 - 24 = 21 R$
Questão 168
Em um país, a primeira etapa para obtenção da carteira de motorista é a contratação de três produtos:
- pacote com 20 aulas teóricas;
- pacote com 10 aulas práticas;
- aluguel do veículo para realização das aulas práticas.
Uma pessoa que pretende obter a carteira de motorista pesquisou o valor do aluguel do veículo e os valores de cada aula teórica e de cada aula prática em três autoescolas. O quadro apresenta esses valores.
| Autoescola | Valor de cada aula teórica (R$) | Valor de cada aula prática (R$) | Aluguel do veículo (R$) |
|---|---|---|---|
| I | 10 | 80 | 400 |
| II | 30 | 50 | 200 |
| III | 20 | 40 | 400 |
Ela contratará os três produtos numa mesma autoescola de modo que o custo total nessa primeira etapa seja o menor possível.
A autoescola que será contratada é a:
A) I, com o custo total de R$ 1 400,00.
B) II, com o custo total de R$ 280,00.
C) II, com o custo total de R$ 1 300,00.
D) III, com o custo total de R$ 460,00.
E) III, com o custo total de R$ 1 200,00.
Raciocínio:
1. Custo total I: 10 ∗ 20 + 80 ∗ 10 + 400 = 200 + 800 + 400 = 1400
2. Custo total II: 30 ∗ 20 + 50 ∗ 10 + 200 = 600 + 500 + 200 = 1300
3. Custo total III: 20 ∗ 20 + 40 ∗ 10 + 400 = 400 + 400 + 400 = 1200
Questão 169
A produtividade de soja em uma área cultivada é a média da quantidade de sacas de 50 quilogramas que são produzidas por hectare. O quadro apresenta a área cultivada e a produtividade de soja em certa propriedade, ao longo de cinco safras, com períodos de um ano, de 2011 a 2016.
| Safra | 11-12 | 12-13 | 13-14 | 14-15 | 15-16 |
|---|---|---|---|---|---|
| Área cultivada (hectare) | 200 | 220 | 250 | 250 | 200 |
| Produtividade (sacas de 50 kg por hectare) | 40 | 30 | 45 | 45 | 50 |
O gráfico de linhas que representa a produção de soja dessa propriedade, em tonelada, nessas cinco safras é:
A) 
B) 
C) 
D) 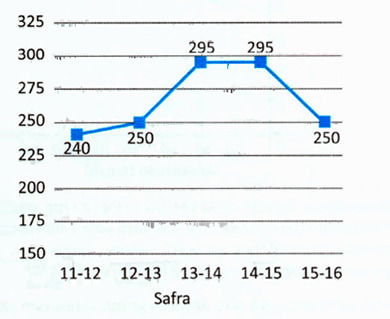
E) 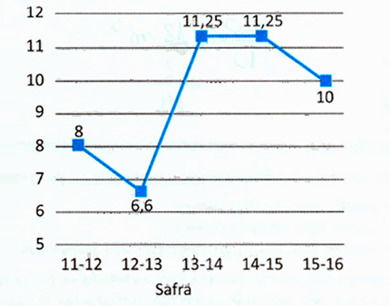
Raciocínio:
Produção (t) = Área (ha) × Produtividade (sacas/ha) × 50 kg/saca ÷ 1000
1. Safra 11-12: 200 × 40 × 50 /1000 = 400 t
2. Safra 12-13: 220 × 30 × 50 /1000 = 330 t
3. Safra 13-14: 250 × 45 × 50 /1000 = 562,5 t
4. Safra 14-15: idem = 562,5 t
5. Safra 15-16: 200 × 50 × 50 /1000 = 500 t
Questão 170
Uma caixa de descarga, acoplada a um vaso sanitário, tem a forma de paralelepípedo reto retângulo cujas dimensões internas da base são 2,5 dm e 1,5 dm. Nessa caixa há uma boia que interrompe o abastecimento quando a altura da coluna de água atinge 2 dm, conforme a figura.
A cada acionamento da descarga, todo o volume de água contida na caixa é despejado no vaso. Para reduzir o volume de água despejado a cada acionamento, uma pessoa colocará, no interior dessa caixa, garrafas de 300 mL, cheias de areia e tampadas, de modo a ficarem submersas quando o abastecimento for interrompido.
Para garantir o funcionamento eficiente, o mínimo de água despejada a cada acionamento deve ser de 5 L.
A quantidade máxima de garrafas que serão colocadas nessa caixa, garantindo um funcionamento eficiente, é igual a
A) 10.
B) 8.
C) 4.
D) 3.
E) 2.
Raciocínio:
1. Volume extra disponível: 7,5 - 5 = 2,5 L
2. Número máximo de garrafas: 2,5 ÷ 0,3 ≈ 8,33 → máximo 8 garrafas
Questão 171
Um confeiteiro passou a produzir tortas em formato de cilindro circular reto, com raio da base variando entre 12 cm e 16 cm e altura de 6 cm. Essas tortas deverão ser embaladas em caixas com formato de prisma reto de base quadrada, de modo que seja possível acomodar a torta em seu interior e ainda restar pelo menos 1 cm de distância entre a torta e as superfícies internas da caixa, lateral e superior.
Ele dispõe, originalmente, de caixas no formato pretendido, cujas dimensões internas são 14 cm de comprimento do lado da base e 7 cm de altura, que não atendem às suas necessidades. Portanto, ele comprará novas caixas, com o mesmo formato das caixas originais, mas com comprimento do lado da base maior, que sejam adequadas para embalar todos os tipos de torta que produz.
A aresta da base das novas caixas deve ser, no mínimo, quantos centímetros maior do que a das caixas originais?
A) 4
B) 12
C) 16
D) 18
E) 20
Raciocínio:
1. Maior torta: raio = 16 cm → diâmetro = 32 cm
2. Margem mínima = 1 cm → lado da base da caixa ≥ 32 + 2 = 34 cm
3. Aumento necessário: 34 - 14 = 20 cm
Questão 172
Um empresário utiliza máquinas cuja pressão interna P, em atmosfera, depende do tempo contínuo de utilização t, em hora, e de um parâmetro positivo K, que define o modelo da máquina, segundo a expressão:
P = 4 log[ −K(t + 1)(t − 19) ]
O fabricante dessas máquinas recomenda ao usuário que a pressão interna desse tipo de máquina não ultrapasse 10 atmosferas durante seu funcionamento.
O empresário pretende comprar novas máquinas desse tipo que deverão funcionar, diariamente, por um período contínuo de 10 horas. Para isso, precisa definir o modelo de máquina a ser adquirida, escolhendo o maior valor possível do parâmetro K, atendendo à recomendação do fabricante.
O maior valor a ser escolhido para K é
A) 100,5
B) 108
C) 102,5/84
D) 102,5/99
E) 25 × 10−2
Raciocínio:
1. Substituindo P = 10 e t = 10:
10 = 4log[−K(10+1)(10−19)] ⟹ 2,5 = log(99K)
2. Aplicando inversão do logaritmo:
Questão 173
Em uma cidade, será construído um túnel que atravessa uma montanha para facilitar o trânsito de automóveis e bicicletas. Dois projetos foram elaborados e os esquemas com as vistas frontais desses projetos são apresentados na figura.
O Projeto 1 conta com dois túneis, um exclusivo para bicicletas e o outro, para automóveis. O Projeto 2 conta com um único túnel, com espaços reservados para o trânsito exclusivo de bicicletas e automóveis. Nos dois projetos, os túneis têm o formato de semicilindro reto de mesma extensão, com vias de ida e volta para os dois tipos de veículos, separados por muretas.
O projeto a ser aprovado será aquele que apresentar a menor área da seção transversal, pois implicará menor volume de material retirado da montanha.
Considere 3 como aproximação para π e desconsidere as espessuras das muretas.
O projeto a ser aprovado é
A) o 1, pois apresenta área de seção transversal medindo 67,5 m².
B) o 2, pois apresenta área de seção transversal medindo 121,5 m².
C) o 1, pois apresenta área de seção transversal medindo 135 m².
D) o 2, pois apresenta área de seção transversal medindo 243 m².
E) qualquer um dos dois, pois apresentam áreas de duas seções transversais com medidas iguais.
Raciocínio:
1. Projeto 1:
2. Projeto 2:
3. Menor área → projeto 1
Questão 174
Um carro que custa 60 mil reais é comercializado por uma revendedora que oferece duas opções de pagamento, todas sem entrada e sem juros:
- opção 1: pagamento em n parcelas iguais;
- opção 2: pagamento em 6 parcelas a mais do que na opção 1 e, com isso, o valor de cada parcela se torna R$ 500,00 menor do que o valor da parcela na opção 1.
Nas duas opções de pagamento, o valor total a ser pago pelo carro é o mesmo.
Qual é a quantidade n de parcelas contidas na opção 1 de pagamento?
A) 18
B) 24
C) 30
D) 42
E) 48
Raciocínio:
1. Equação:
2. Multiplicando e resolvendo:
60 000n = (60 000 − 500n) (n + 6) ⟹ 500n2 + 3000n − 360 000 = 0 ⟹ n2 + 6n − 720 =0
3. Solução positiva: n = 24
Questão 175
Um pai comprou oito presentes diferentes (dentre os quais, uma bicicleta e um celular) para dar a seus três filhos. Ele pretende distribuir os presentes de modo que o filho mais velho e o mais novo recebam três presentes cada um, e o do meio receba os dois presentes restantes. O mais velho ganhará, entre seus presentes, ou uma bicicleta ou um celular, mas não ambos.
De quantas maneiras distintas a distribuição dos presentes pode ser feita?
A) 36
B) 53
C) 300
D) 360
E) 560
Raciocínio:
1. Separar casos: filho mais velho recebe bicicleta ou celular → 2 situações
2. Contagem combinatória:
- Escolher 3 presentes do total de 8 para o filho mais velho com a condição (bicicleta ou celular, mas não ambos) → 150 maneiras para cada caso
- Somando as duas situações: 150 + 150 = 300 maneiras
Questão 176
A final de um campeonato de futebol foi disputada em 2 tempos regulamentares, de 45 minutos cada, sem acréscimos, com uma prorrogação de 30 minutos, também sem acréscimos. Um jogador entrou no início do segundo tempo, com um equipamento para medir a distância percorrida durante sua participação no jogo. Ao final do segundo tempo regulamentar, esse jogador havia percorrido 4,5 km. Ele manteve na prorrogação a mesma velocidade média que havia mantido no segundo tempo regulamentar.
A distância percorrida por esse jogador durante sua participação na partida, em quilômetro, foi
A) 4,5.
B) 6,0.
C) 7,5.
D) 9,0.
E) 12,0.
Raciocínio:
1. Velocidade média:
2. Tempo total de participação: 45 + 30 = 75 min
3. Distância total:
D = v ⋅ 75 = 0,1 ⋅ 75 = 7,5 km
Questão 177
A figura ilustra o projeto visual para confecção de uma medalha comemorativa, com a forma de um cilindro circular reto, de diâmetro 6 cm e espessura 3 mm.
A figura ABCD tem a forma de um quadrado e é a base de um prisma que atravessa toda a medalha. A região da medalha externa a esse prisma será cunhada em ouro. Pretende-se cunhar 100 dessas medalhas.
Considere 3,1 como valor aproximado para π.
Qual é o volume de ouro, em centímetro cúbico, necessário para a confecção dessas medalhas?
A) 288
B) 297
C) 567
D) 990
E) 1134
Raciocínio:
1. Volume da moeda:
Vmoeda = πr2h = 3,1 ⋅ 32 ⋅ 0,3 = 8,37 cm³
2. Lado do quadrado:
3. Volume do prisma:
Vprisma = l2h = 18 ⋅ 0,3 = 5,4 cm³
4. Volume de ouro por medalha:
Vouro = 8,37 − 5,4 = 2,97 cm³
5. Total para 100 medalhas:
100 ⋅ 2,97 ≈ 297 cm³
Questão 178
Três dados cúbicos, com faces numeradas de 1 a 6, foram utilizados em um jogo. Artur escolheu dois dados, e João ficou com o terceiro. O jogo consiste em ambos lançarem seus dados, observarem os números nas faces voltadas para cima e compararem o maior número obtido por Artur com o número obtido por João. Vence o jogador que obtiver o maior número. Em caso de empate, a vitória é de João.
O jogador que tem a maior probabilidade de vitória é
A) Artur, com probabilidade de 2/3.
B) João, com probabilidade de 4/9.
C) Artur, com probabilidade de 91/216.
D) João, com probabilidade de 91/216.
E) Artur, com probabilidade de 125/216.
Raciocínio:
1. Probabilidade de João vencer:
2. Probabilidade de Artur vencer:
Questão 179
A luminância de um objeto é a grandeza que descreve a quantidade de luz produzida ou refletida por sua superfície. Ela está definida como a razão entre a intensidade luminosa, medida em candela (cd), e o quadrado da distância do objeto até o foco de luz, medida em metro (m).
A unidade de medida da luminância de um objeto é
A) cd/m²
B) m²/cd
C) cd/m
D) m/cd
E) m/cd²
Enunciado resumido:
- Luminância = intensidade luminosa / distância²
- Intensidade luminosa: cd, distância: m
Raciocínio:
Questão 180
Quatro amigos, cada um com 100 moedas, criaram um jogo, no qual cada um assume uma das quatro posições 1, 2, 3 ou 4, indicadas na figura, e nela permanece até o final.
O desenvolvimento do jogo se dá em rodadas e, em todas elas, cada jogador transfere e recebe uma quantidade de moedas da seguinte maneira:
• o jogador na posição 1 transfere 1 moeda para o jogador na posição 2;
• o jogador na posição 2 transfere 2 moedas para o jogador na posição 3;
• o jogador na posição 3 transfere 3 moedas para o jogador na posição 4;
• o jogador na posição 4 transfere 4 moedas para o jogador na posição 1, completando a rodada.
Ao final da rodada n, qual é a expressão algébrica que representa o número de moedas do jogador na posição 1?
A) 103 + 4n
B) 103 + 3n
C) 100 + 4n
D) 100 + 3n
E) 99 + 4n
Enunciado resumido:
4 amigos, cada um 100 moedas
Cada rodada:
- Posição 1 → 1 moeda para 2
- Posição 2 → 2 moedas para 3
- Posição 3 → 3 moedas para 4
- Posição 4 → 4 moedas para 1
Pergunta: expressão para moedas da posição 1 após n rodadas
Raciocínio:
1. Posição 1: perde 1, recebe 4 → aumenta 3 moedas por rodada
2. Moedas após n rodadas:
100 + 3n
Gabarito oficial - PROVA AZUL

Gabarito oficial - PROVA AMARELA

Gabarito oficial - PROVA CINZA

Gabarito oficial - PROVA VERDE

Confira também os gabaritos explicados da Prova de Linguagens e Ciências Humanas ENEM 2025.
MATÉRIA, Equipe. Prova de Matemática e Ciências da Natureza ENEM 2025 (com gabarito explicado). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/prova-de-matematica-e-ciencias-da-natureza-enem-2025-com-gabarito-explicado/. Acesso em:


