Quantidade de Movimento

Rosimar Gouveia

Professora de Matemática e Física

A quantidade de movimento, também chamada de momento linear, é uma grandeza vetorial definida como o produto da massa de um corpo pela sua velocidade.

A direção e o sentido do momento linear são dados pela direção e o sentido da velocidade.

Verifica-se que a quantidade de movimento se conserva, e este fato é empregado em inúmeras situações do cotidiano.

Sendo fundamental no estudo das interações de curta duração, como por exemplos nos choques e colisões.

Podemos constatar a conservação da quantidade de movimento, observando um pêndulo de Newton.

Ao deslocar e soltar uma das esferas do pêndulo a uma certa altura, ela irá colidir com as demais esferas.

Todas permanecerão em repouso, com exceção da esfera da outra extremidade que sofrerá um deslocamento, alcançando a mesma altura da esfera que deslocamos.

Fórmula

A quantidade de movimento é representada pela letra Q, sendo calculada usando-se a seguinte fórmula:

Onde,

Q: quantidade de movimento (kg.m/s)
m: massa (kg)
v: velocidade (m/s)

Exemplo:

Uma bola de 400 g se movimenta num dado instante, conforme figura abaixo, com velocidade de módulo igual a 2 m/s. Qual o módulo, a direção e o sentido da quantidade de movimento da bola no referido momento?

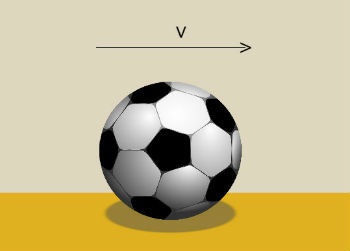
Solução:

Para calcular a quantidade de movimento, basta multiplicar a velocidade da bola, por sua massa. Entretanto, devemos transformar as unidades para o sistema internacional.

m = 400 g = 0,4 kg

Substituindo, temos:

Q = 0,4 . 2 = 0,8 kg.m/s

A direção e o sentido da quantidade de movimento serão os mesmos da velocidade, ou seja, direção horizontal e sentido da esquerda para a direita.

Impulso e Quantidade de Movimento

Além do momento linear, existe também uma outra grandeza física associada ao movimento chamada de impulso.

Definida como o produto da força por um intervalo de tempo, o impulso é uma grandeza vetorial.

Assim, a fórmula do impulso é:

Onde,

I: impulso (N.s)
F: força (N)
Δt: intervalo de tempo

Teorema do Impulso

Considerando um corpo submetido a uma força resultante constante e de mesma direção da velocidade, podemos usar a 2ª Lei de Newton (F = m . a) e substituir a força na fórmula anterior.

Então, o impulso pode ser determinado por: I = m . a . Δt. Lembrando que a aceleração é igual a variação da velocidade num intervalo de tempo, então, teremos que:

I = m . Δv

Daí, encontramos a relação entre impulso e quantidade de movimento, ou seja, o impulso é igual a variação da quantidade de movimento e pode ser expresso como:

Exemplo:

Um corpo de massa igual a 1 kg apresenta, em um dado instante, velocidade de 5 m/s, quando passa a atuar sobre ele uma força de intensidade igual a 5N, na mesma direção e sentido da velocidade, durante 4s. Determine o valor da velocidade do corpo ao final dos 4s.

Solução:

Lembrando que:

I = F . Δt e ΔQ = m . Δv = m . v - m . v₀

Pelo teorema do impulso, podemos escrever:

F . Δt = m . v - m . v₀
5 . 4 = 1 . v - 1 . 5
v = 20 + 5
v = 25 m/s

Conservação da Quantidade de Movimento

Em um sistema sem atuação de forças externas, ou que a intensidade destas forças é muito pequena comparada com a intensidade das forças internas, o impulso será igual a zero.

Pelo teorema do impulso, a variação da quantidade de movimento também será igual a zero, ou seja, a quantidade de movimento é constante.

Portanto, em um sistema isolado de forças externas a quantidade de movimento se conserva. Este é o princípio da conservação da quantidade de movimento.

Podemos aplicar esse princípio em choques ou explosões, pois nessas situações as forças internas são muito maiores que as forças externas ao sistema.

As colisões que acontecem entre as bolas em um jogo de bilhar, são exemplos de situações em que a quantidade de movimento se conserva.

Exemplo:

Em um ringue de patinação no gelo, dois patinadores, um de 40 kg e outro de 60 kg, estão parados um em frente ao outro. Um deles resolve empurrar o outro e ambos passam a se movimentar em sentidos opostos. Sabendo que o patinador de 60 kg adquire velocidade de 4 m/s, determine a velocidade adquirida pelo outro patinador.

Solução:

Como o sistema formado pelos dois patinadores é isolado de forças externas, a quantidade de movimento inicial será igual a quantidade de movimento após o empurrão.
Logo, a quantidade de movimento final será igual a zero, pois inicialmente os dois estavam em repouso. Então:

Q_f = Q_i = 0

A quantidade de movimento final é igual a soma vetorial da quantidade de movimento de cada patinador, neste caso teremos:

Como as velocidades apresentam sentidos opostos, vamos indicar uma delas com sinal de (-), assim:

M . V - m . v = 0

Substituindo os valores:

Aprenda também sobre impulso.

Exercícios Resolvidos

1) Enem - 2014

Durante um reparo na estação espacial internacional, um cosmonauta, de massa 90 kg, substitui uma bomba do sistema de refrigeração, de massa 360 kg, que estava danificada. Inicialmente, o cosmonauta e a bomba estão em repouso em relação à estação. Quando ele empurra a bomba para o espaço, ele é empurrado no sentido oposto. Nesse processo, a bomba adquire uma velocidade de 0,2 m/s em relação à estação.

Qual é o valor da velocidade escalar adquirida pelo cosmonauta, em relação à estação, após o empurrão?

a) 0,05 m/s
b) 0,20 m/s
c) 0,40 m/s
d) 0,50 m/s
e) 0,80 m/s

2) Enem - 2016

O trilho de ar é um dispositivo utilizado em laboratórios de física para analisar movimentos em que corpos de prova (carrinhos) podem se mover com atrito desprezível. A figura ilustra um trilho horizontal com dois carrinhos (1 e 2) em que se realiza um experimento para obter a massa do carrinho 2. No instante em que o carrinho 1, de massa 150,0 g, passa a se mover com velocidade escalar constante, o carrinho 2 está em repouso. No momento em que o carrinho 1 se choca com o carrinho 2, ambos passam a se movimentar juntos com velocidade escalar constante. Os sensores eletrônicos distribuídos ao longo do trilho determinam as posições e registram os instantes associados à passagem de cada carrinho, gerando os dados do quadro.

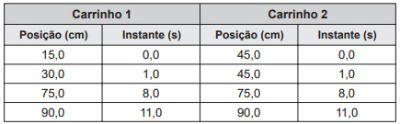
Com base nos dados experimentais, o valor da massa do carrinho 2 é igual a

a) 50,0 g
b) 250,0 g
c) 300,0 g
d) 450,0 g
e) 600,0 g

Veja também: Fórmulas de Cinemática

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.