Exercícios de Eletrostática (com questões resolvidas e comentadas)

Rafael C. Asth

Professor de Matemática e Física

Eletrostática é a área da Física que estuda as interações entre cargas elétricas. Os processos de eletrização, a força elétrica que surge entre duas cargas e as características do campo ao redor de um corpo eletrizado, são alguns dos assuntos tratados.

Aproveite os exercícios comentados e resolvidos para fazer uma revisão desta importante área.

Questão 1

Duas pequenas esferas, cada uma com uma carga de $2 sinal de multiplicação 10 à potência de menos 6 fim do exponencial espaço espaço$ Coulomb, estão separadas por uma distância de 3 metros no vácuo. Utilizando a constante eletrostática $reto k igual a 9 sinal de multiplicação 10 à potência de 9 espaço reto N vezes reto m ao quadrado dividido por reto C ao quadrado espaço espaço$ , calcule a força elétrica entre elas.

a) $4 sinal de multiplicação 10 à potência de menos 3 fim do exponencial espaço reto N$

b) $4 sinal de multiplicação 10 à potência de menos 2 fim do exponencial espaço reto N$

c) $4 sinal de multiplicação 10 à potência de menos 1 fim do exponencial espaço reto N$

d) $4 sinal de multiplicação 10 à potência de 0 espaço reto N$

e) $4 sinal de multiplicação 10 à potência de 1 espaço reto N$

Questão 2

Uma carga pontual $reto q igual a menos 3 sinal de multiplicação 10 à potência de menos 6 fim do exponencial espaço reto C$ está localizada no vácuo. Calcule o campo elétrico gerado por essa carga a uma distância de 2 m da carga.

Considere a constante eletrostática do vácuo $reto k igual a 9 sinal de multiplicação 10 à potência de 9 espaço reto N vezes reto m ao quadrado dividido por reto C ao quadrado espaço espaço$ .

a) $menos 6 vírgula 75 sinal de multiplicação 10 ao cubo espaço reto N dividido por reto C$

b) $6 vírgula 75 sinal de multiplicação 10 ao cubo espaço reto N dividido por reto C$

c) $menos 1 vírgula 35 sinal de multiplicação 10 ao cubo espaço reto N dividido por reto C$

d) $1 vírgula 35 sinal de multiplicação 10 à potência de 4 espaço reto N dividido por reto C$

e) $1 vírgula 35 sinal de multiplicação 10 ao cubo espaço reto N dividido por reto C$

Questão 3

(UERJ - 2019) Na ilustração, estão representados os pontos I, II, III e IV em um campo elétrico uniforme.

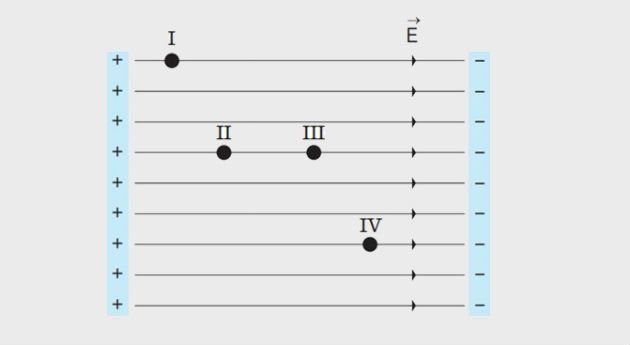
Uma partícula de massa desprezível e carga positiva adquire a maior energia potencial elétrica possível se for colocada no ponto:

a) I
b) II
c) III
d) IV

Ver Resposta

Alternativa: a) I

Uma carga positiva, ao ser colocada em um campo elétrico uniforme, terá sua energia potencial diminuída a medida que percorre o campo elétrico no mesmo sentido das linhas de força.

Assim, a energia potencial diminui a medida em que a partícula se afasta do polo positivo e se aproxima do negativo.

Neste caso, no ponto I, a carga terá mais energia potencial elétrica do que nos demais pontos.

Questão 4

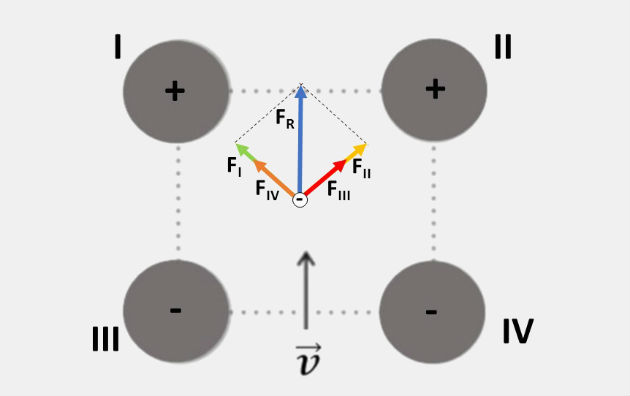
(Fuvest - 2016) Os centros de quatro esferas idênticas, I, II, III e IV, com distribuições uniformes de carga, formam um quadrado. Um feixe de elétrons penetra na região delimitada por esse quadrado, pelo ponto equidistante dos centros das esferas III e IV, com velocidade inicial $v com seta para a direita sobrescrito$ na direção perpendicular à reta que une os centros de III e IV, conforme representado a figura.

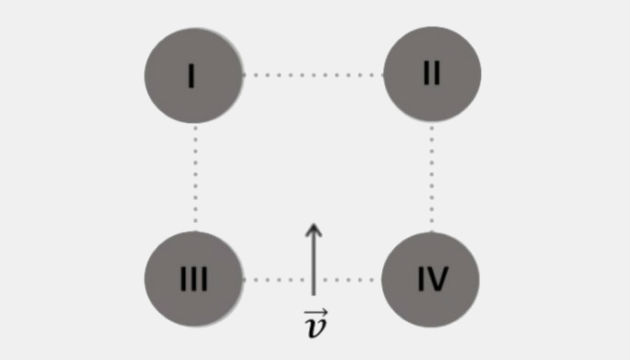
A trajetória dos elétrons será retilínea, na direção de $v com seta para a direita sobrescrito$ , e eles serão acelerados com velocidade crescente dentro da região plana delimitada pelo quadrado, se as esferas I, II, III e IV estiverem, respectivamente, eletrizadas (Note e adote: Q é um número positivo)

a) + Q, - Q, - Q, + Q
b) + 2Q, - Q, + Q, - 2Q
c) + Q, + Q, - Q, - Q
d) - Q, - Q, + Q, + Q
e) + Q, + 2Q, - 2Q, - Q

Ver Resposta

Alternativa: c) + Q, + Q, - Q, - Q

Para que o feixe de elétrons seja acelerado com velocidade crescente, é necessário que exista uma força resultante atuando sobre eles.

Esse força será a resultante vetorial da interação entre o feixe e as forças exercidas por cada carga posicionada nos vértices do quadrado.

Sendo assim, a força resultante deverá ter mesma direção e sentido do vetor $v com seta para a direita sobrescrito$ indicado na figura da questão.

Posicionando um elétron no interior do quadrado, vamos definir inicialmente a força resultante em função da presença das cargas I e II.

Para que a força resultante aponte para o sentido indicado, as forças F_I e F_IIdeverão ser de atração. Caso fosse de repulsão, a força resultante apontaria para baixo.

Desta forma, as cargas I e II deverão ser positivas, já que a carga do elétron é negativa.

Pela presença das cargas III e IV surgirá as forças F_IIIe F_IV , sendo que deverão ser de repulsão, para que a força resultante tenha o sentido esperado. Desta forma, essas cargas serão negativas.

Na imagem abaixo, temos a indicação dessas forças:

Questão 5

(UFRGS - 2016) Uma esfera condutora e isolada, de raio R, foi carregada com uma carga elétrica Q. Considerando o regime estacionário, assinale o gráfico abaixo que melhor representa o valor do potencial elétrico dentro da esfera, como função da distância r < R até o centro da esfera.

Ver Resposta

Alternativa: a)

Em um condutor eletrizado, as cargas em excesso ficam localizadas na superfície externa do condutor. Desta forma, no interior do condutor o campo elétrico é nulo, e o potencial, em todos os pontos no seu interior, terá o mesmo valor.

Sendo assim, o gráfico que representa corretamente esta situação é o que indica o potencial constante.

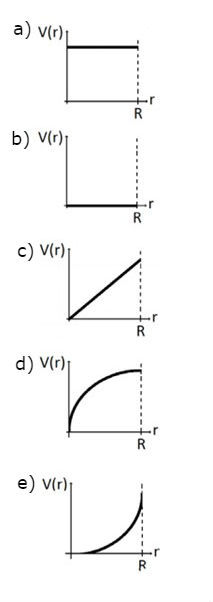
Questão 6

(Unesp - 2015) Modelos elétricos são frequentemente utilizados para explicar a transmissão de informações em diversos sistemas do corpo humano. O sistema nervoso, por exemplo, é composto por neurônios (figura 1), células delimitadas por uma fina membrana lipoproteica que separa o meio intracelular do meio extracelular. A parte interna da membrana é negativamente carregada e a parte externa possui carga positiva (figura 2), de maneira análoga ao que ocorre nas placas de um capacitor.

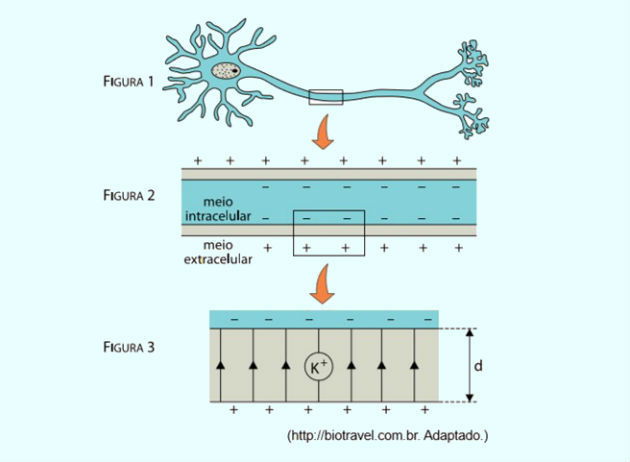
A figura 3 representa um fragmento ampliado dessa membrana, de espessura d, que está sob ação de um campo elétrico uniforme, representado na figura por suas linhas de força paralelas entre si e orientadas para cima. A diferença de potencial entre o meio intracelular e o extracelular é V. Considerando a carga elétrica elementar como e, o íon de potássio K+, indicado na figura 3, sob ação desse campo elétrico, ficaria sujeito a uma força elétrica cujo módulo pode ser escrito por

$a parêntese direito espaço e. V. d b parêntese direito espaço numerador e. d sobre denominador V fim da fração c parêntese direito espaço numerador V. d sobre denominador e fim da fração d parêntese direito espaço numerador e sobre denominador V. d fim da fração e parêntese direito espaço numerador e. V sobre denominador d fim da fração$

Ver Resposta

Alternativa: e) $numerador e. V sobre denominador d fim da fração$

O valor da força elétrica é encontrado através da seguinte fórmula:

$F igual a q. E$

Por sua vez, em um campo elétrico uniforme, a fórmula para o calculo da diferença de potencial é igual a:

$V igual a E. d seta dupla para a direita E igual a V sobre d$

Substituindo essa expressão na fórmula da força, temos:

$F igual a q. V sobre d$

Considerando q igual a carga elementar e, a expressão ficará:

$F igual a numerador e. V sobre denominador d fim da fração$

$numerador e. V sobre denominador d fim da fração$

Veja também: Força Elétrica

Questão 7

(UFRGS - 2014) Considere dois balões de borracha, A e B. O balão B tem excesso de cargas negativas; o balão A, ao ser aproximado do balão B, é repelido por ele. Por outro lado, quando certo objeto metálico isolado é aproximado do balão A, este é atraído pelo objeto.

Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem em que aparecem.

A respeito das cargas elétricas líquidas no balão A e no objeto, pode-se concluir que o balão A só pode _______ e que o objeto só pode _______ .

a) ter excesso de cargas negativas – ter excesso de cargas positivas
b) ter excesso de cargas negativas – ter excesso de cargas positivas ou estar eletricamente neutro
c) ter excesso de cargas negativas – estar eletricamente neutro
d) estar eletricamente neutro – ter excesso de cargas positivas ou estar eletricamente neutro
e) estar eletricamente neutro – ter excesso de cargas positivas

Ver Resposta

Alternativa: b) ter excesso de cargas negativas – ter excesso de cargas positivas ou estar eletricamente neutro

Quando dois corpos estão carregados eletricamente com cargas de sinais contrários, ao se aproximarem surgirá entre eles uma força de atração.

Ao contrário, se suas cargas tiverem mesmo sinal, a força será de repulsão. Quando um corpo neutro se aproxima de um corpo eletrizado, a força entre eles será de atração, independente do sinal da carga.

Sendo assim, como o balão A foi repelido pelo balão B, sua carga será igual a de B, ou seja, possui excesso de cargas negativas.

Agora que sabemos a carga do balão A, podemos descobrir a carga do objeto. Como a força é atrativa, então temos duas possibilidades: o objeto pode ser neutro ou apresentar carga contrária do balão A.

Desta forma, o objeto pode estar neutro ou carregado positivamente.

Questão 8

(Udesc - 2013) Duas esferas idênticas, A e B, feitas de material condutor, apresentam as cargas +3ē e -5ē, e são colocadas em contato. Após o equilíbrio, a esfera A é colocada em contato com outra esfera idêntica C, a qual possui carga elétrica de +3ē. Assinale a alternativa que contém o valor da carga elétrica final da esfera A.

a) +2ē
b) -1ē
c) +1ē
d) -2ē
e) 0ē

Ver Resposta

Alternativa: c) +1ē

Quando duas esferas condutoras idênticas são colocadas em contato, ocorre uma redistribuição das cargas. Ao serem novamente separadas, cada uma dela ficará com metade da cargas totais.

Sendo assim, após o contato entre a esfera A e a esfera B, cada uma das esferas terá de carga:

$Q com A B subscrito fim do subscrito igual a numerador mais 3 e em moldura superior mais parêntese esquerdo menos 5 e em moldura superior parêntese direito sobre denominador 2 fim da fração igual a numerador menos 2 e com barra sobrescrito sobre denominador 2 fim da fração igual a menos pilha 1 e com barra acima$

Então, a esfera A passou a ter carga igual a - ē. Fazendo novo contato, agora com a esfera C, sua carga final será encontrada fazendo-se:

$Q com A C subscrito fim do subscrito igual a numerador menos 1 e com barra sobrescrito mais parêntese esquerdo mais 3 e com barra sobrescrito parêntese direito sobre denominador 2 fim da fração igual a numerador mais 2 e em moldura superior sobre denominador 2 fim da fração igual a mais 1 e em moldura superior fecha moldura$

Questão 9

(Enem - 2010) Duas irmãs que dividem o meso quarto de estudos combinaram de comprar duas caixas com tampas para guardarem seus pertences dentro de suas caixas, evitando, assim, a bagunça sobre a mesa de estudos. Uma delas comprou uma metálica, e a outra, uma caixa de madeira de área e espessura lateral diferentes, para facilitar a identificação. Um dia as meninas foram estudar para a prova de Física e, ao se acomodarem na mesa de estudos, guardaram seus celulares ligados dentro de suas caixas. Ao longo desse dia, uma delas recebeu ligações telefônicas, enquanto os amigos da outra tentavam ligar e recebiam a mensagem de que o celular estava fora da área de cobertura ou desligado.

Para explicar essa situação, um físico deveria afirmar que o material da caixa, cujo telefone celular não recebeu as ligações é de

a) madeira, e o telefone não funcionava porque a madeira não é um bom condutor de eletricidade.
b) metal, e o telefone não funcionava devido à blindagem eletrostática que o metal proporcionava.
c) metal, e o telefone não funcionava porque o metal refletia todo tipo de radiação que nele incidia.
d) metal, e o telefone não funcionava porque a área lateral da caixa de metal era maior.
e) madeira, e o telefone não funcionava porque a espessura desta caixa era maior que a espessura da caixa de metal.

Ver Resposta

Alternativa: b) metal, e o telefone não funcionava devido à blindagem eletrostática que o metal proporcionava.

Os materiais metálicos são bons condutores de cargas, sendo assim, em uma caixa de metal os elétrons livres ficarão distribuídos na sua parte externa.

Dentro da caixa o valor do campo elétrico é nulo. Este fato é chamado de blindagem eletrostática e foi comprovado por Michael Faraday, em uma experiência que ficou conhecida como gaiola de Faraday.

Para saber mais, veja também:

Veja também exercícios de Física (resolvidos) para 3º ano do ensino.

Referências Bibliográficas

Halliday, D., Resnick, R., & Walker, J. (Ano de Publicação). Fundamentos de Física: Eletromagnetismo (Vol. 3). Rio de Janeiro: LTC.

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.