Exercícios de Campo Elétrico

Rosimar Gouveia

Professora de Matemática e Física

O campo elétrico representa a modificação ocorrida no espaço ao redor de uma carga elétrica. Ele é representado por linhas chamadas de linhas de força.

Este assunto faz parte do conteúdo de eletrostática. Então, aproveite os exercícios que o Toda Matéria preparou para você, teste seus conhecimentos e tire dúvidas acompanhando as resoluções comentadas.

Questões resolvidas e comentadas

1) UFRGS - 2019

Na figura abaixo, está representado, em corte, um sistema de três cargas elétricas com seu respectivo conjunto de superfícies equipotenciais.

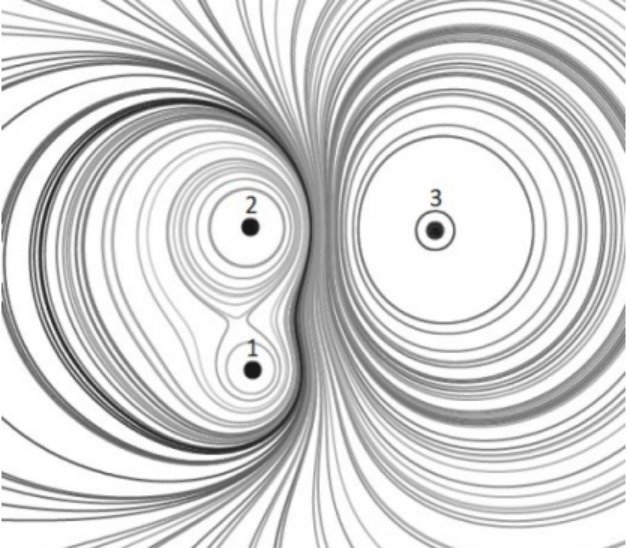
Questão campo elétrico UFRGS 2019

Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem em que aparecem. A partir do traçado das equipotenciais, pode-se afirmar que as cargas ........ têm sinais ........ e que os módulos das cargas são tais que ........ .

a) 1 e 2 – iguais – q1 < q2 < q3
b) 1 e 3 – iguais – q1 < q2 < q3
c) 1 e 2 – opostos – q1 < q2 < q3
d) 2 e 3 – opostos – q1 > q2 > q3
e) 2 e 3 – iguais – q1 > q2 > q3

Ver Resposta

As superfícies equipotenciais representam superfícies formadas por pontos que possuem o mesmo potencial elétrico.

Observando o desenho identificamos que entre as cargas 1 e 2 existem superfícies comuns, isso acontece quando as cargas possuem mesmo sinal. Portanto, 1 e 2 possuem cargas iguais.

Pelo desenho observamos, ainda, que a carga 1 é a que possui menor módulo de carga, pois apresenta o menor número de superfícies e que a carga 3 é a que apresenta maior número.

Sendo assim, temos que q1 < q2 < q3.

Alternativa: a) 1 e 2 – iguais – q1 < q2 < q3

2) UERJ - 2019

Na ilustração, estão representados os pontos I, II, III e IV em um campo elétrico uniforme.

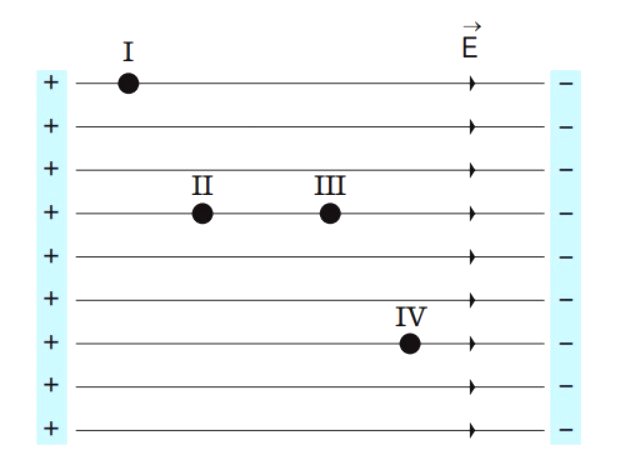
Uma partícula de massa desprezível e carga positiva adquire a maior energia potencial elétrica possível se for colocada no ponto:

a) I
b) II
c) III
d) IV

Ver Resposta

Em um campo elétrico uniforme, uma partícula positiva está com maior energia potencial elétrica quanto mais próxima estiver da placa positiva.

Neste caso, o ponto I é o que a carga terá maior energia potencial.

Alternativa: a) I

3) UECE - 2016

Precipitador eletrostático é um equipamento que pode ser utilizado para remoção de pequenas partículas presentes nos gases de exaustão em chaminés industriais. O princípio básico de funcionamento do equipamento é a ionização dessas partículas, seguida de remoção pelo uso de um campo elétrico na região de passagem delas. Suponha que uma delas tenha massa m, adquira uma carga de valor q e fique submetida a um campo elétrico de módulo E. A força elétrica sobre essa partícula é dada por

a) mqE.
b) mE/qb.
c) q/E.
d) qE.

Ver Resposta

A intensidade da força elétrica que atua em uma carga situada em uma região onde existe um campo elétrico é igual ao produto da carga pelo módulo do campo elétrico, ou seja F = q.E.

Alternativa: d) qE

4) Fuvest - 2015

Em uma aula de laboratório de Física, para estudar propriedades de cargas elétricas, foi realizado um experimento em que pequenas esferas eletrizadas são injetadas na parte superior de uma câmara, em vácuo, onde há um campo elétrico uniforme na mesma direção e sentido da aceleração local da gravidade. Observou-se que, com campo elétrico de módulo igual a 2 x 10³ V/m, uma das esferas, de massa 3,2 x 10^-15 kg, permanecia com velocidade constante no interior da câmara. Essa esfera tem (considere: carga do elétron = - 1,6 x 10^-19 C; carga do próton = + 1,6 x 10^-19 C; aceleração local da gravidade = 10 m/s²)

a) o mesmo número de elétrons e de prótons.
b) 100 elétrons a mais que prótons.
c) 100 elétrons a menos que prótons.
d) 2000 elétrons a mais que prótons.
e) 2000 elétrons a menos que prótons.

Ver Resposta

De acordo com as informações do problema, identificamos que as forças que atuam na esfera são a força peso e a força elétrica.

Como a esfera permanece no câmara com velocidade constante, concluímos que essas duas forças apresentam mesmo módulo e sentido contrário. Conforme imagem abaixo:

Desta forma, podemos calcular o módulo da carga igualando as duas forças que atuam na esfera, ou seja:

$F com e subscrito igual a P q. E igual a m. g q.2.10 ao cubo igual a 3 vírgula 2.10 à potência de menos 15 fim do exponencial.10 q igual a numerador 3 vírgula 2.10 à potência de menos 14 fim do exponencial sobre denominador 2.10 ao cubo fim da fração q igual a 1 vírgula 6.10 à potência de menos 17 fim do exponencial C$

Agora, para encontrar o número de partículas a mais, vamos usar a seguinte relação:

q = n.e

sendo,

n: número de elétrons ou prótons a mais
e: carga elementar

Portanto, substituindo os valores indicados no problema, temos:

$1 vírgula 6.10 à potência de menos 17 fim do exponencial igual a n.1 vírgula 6.10 à potência de menos 19 fim do exponencial n igual a numerador 1 vírgula 6.10 à potência de menos 17 fim do exponencial sobre denominador 1 vírgula 6.10 à potência de menos 19 fim do exponencial fim da fração n igual a 10 à potência de menos 17 menos parêntese esquerdo menos 19 parêntese direito fim do exponencial n igual a 10 ao quadrado espaço p a r t í c u l a s$

Como vimos, a força elétrica terá que ter o sentido oposto da força peso.

Para que isso ocorra é necessário que a carga tenha sinal negativo, pois desta forma a força elétrica e o campo elétrico também terão sentidos opostos.

Sendo assim, a esfera terá que ter um maior número de elétrons do que de prótons.

Alternativa: b) 100 elétrons a mais que prótons.

5) Unesp - 2015

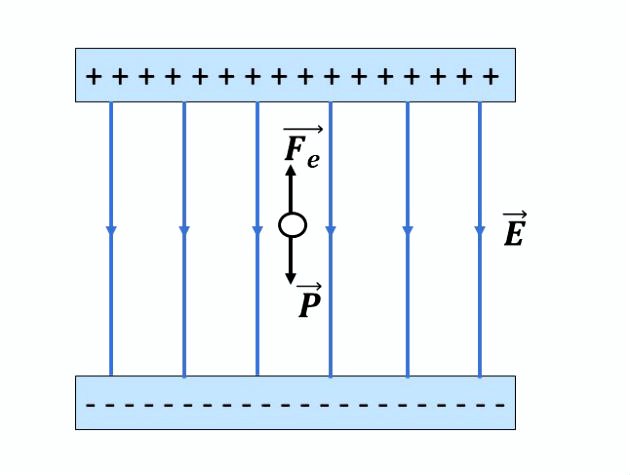
Modelos elétricos são frequentemente utilizados para explicar a transmissão de informações em diversos sistemas do corpo humano. O sistema nervoso, por exemplo, é composto por neurônios (figura 1), células delimitadas por uma fina membrana lipoproteica que separa o meio intracelular do meio extracelular. A parte interna da membrana é negativamente carregada e a parte externa possui carga positiva (figura 2), de maneira análoga ao que ocorre nas placas de um capacitor.

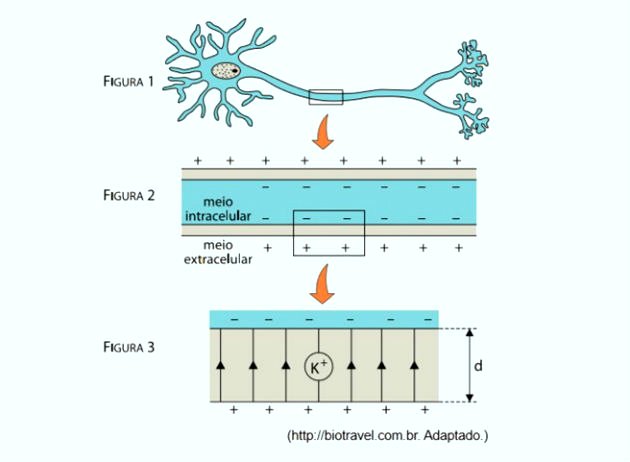
A figura 3 representa um fragmento ampliado dessa membrana, de espessura d, que está sob ação de um campo elétrico uniforme, representado na figura por suas linhas de força paralelas entre si e orientadas para cima. A diferença de potencial entre o meio intracelular e o extracelular é V. Considerando a carga elétrica elementar como e, o íon de potássio K+, indicado na figura 3, sob ação desse campo elétrico, ficaria sujeito a uma força elétrica cujo módulo pode ser escrito por

$a parêntese direito espaço e. V. d b parêntese direito numerador e. d sobre denominador V fim da fração c parêntese direito numerador V. d sobre denominador e fim da fração d parêntese direito numerador e sobre denominador V. d fim da fração e parêntese direito numerador e. V sobre denominador d fim da fração$

Ver Resposta

Em um campo elétrico uniforme a diferença de potencial é dada por:

$V igual a E. d$

O campo elétrico E é igual a razão entre a força elétrica e a carga, ou seja:

$E igual a F sobre q$

Substituindo essa relação na relação anterior, temos:

$V igual a F sobre q. d$

Como temos apenas um íon de potássio, a expressão q =n.e ficará q=e. Substituindo esse valor na expressão anterior e isolando a força, encontramos:

$F igual a numerador e. V sobre denominador d fim da fração$

Alternativa: d) $F igual a numerador e. V sobre denominador d fim da fração$

6) Fuvest - 2015

A região entre duas placas metálicas, planas e paralelas está esquematizada na figura ao lado. As linhas tracejadas representam o campo elétrico uniforme existente entre as placas. A distância entre as placas é 5 mm e a diferença de potencial entre elas é 300 V. As coordenadas dos pontos A, B e C são mostradas na figura. (Anote e adote: O sistema está no vácuo. Carga do elétron = -1,6.10^-19 C)

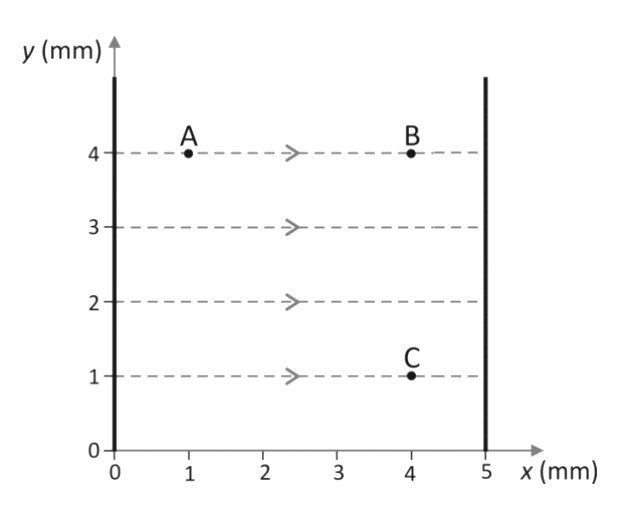
Determine

a) os módulos E_A, E_B e E_C do campo elétrico nos pontos A, B e C, respectivamente;

b) as diferenças de potencial V_AB e V_BC entre os pontos A e B e entre os pontos B e C, respectivamente;

c) o trabalho $tau$ realizado pela força elétrica sobre um elétron que se desloca do ponto C ao ponto A.

Ver Resposta

a) Como o campo elétrico entre as placas é uniforme, o valor será o mesmo nos pontos A, B e C, ou seja, E_A = E_B = E_C = E .

Para calcular o módulo de E, iremos aplicar a seguinte fórmula:

V= E.d

Sendo V = 300 V e d= 5 mm = 0,005 m, vamos encontrar o seguinte valor:

$300 igual a 0 vírgula 005. E E igual a numerador 300 sobre denominador 0 vírgula 005 fim da fração E igual a 60 espaço 000 igual a 6 vírgula 0.10 à potência de 4 V dividido por m$

b) Para calcular as diferenças de potencial dos pontos indicados, vamos aplicar a mesma fórmula anterior, considerando as distâncias indicadas, ou seja:

$V com A B subscrito fim do subscrito igual a E. d com A B subscrito fim do subscrito V com A B subscrito fim do subscrito igual a 60 espaço 000. parêntese esquerdo 0 vírgula 004 menos 0 vírgula 001 parêntese direito V com A B subscrito fim do subscrito igual a 60 espaço 000.0 vírgula 003 V com A B espaço subscrito fim do subscrito igual a 180 espaço V$

Agora vamos calcular a diferença de potencial entre os pontos B e C. Para isso, note que esses dois pontos estão a uma mesma distância das placas, ou seja, d_BC= 0,004 - 0,004 = 0.

Desta forma, a diferença de potencial será igual a zero, isto é:

V_BC = 60 000 . 0 = 0

c) Para calcular o trabalho, usaremos a seguinte fórmula:

$tau igual a q parêntese esquerdo V com c subscrito menos V com A subscrito parêntese direito$

Sendo o potencial do ponto C igual ao do ponto B, então V_c - V_A = V_B - V_A = - V_AB = - 180 V. Substituindo esse valor na fórmula, temos:

$tau igual a menos 1 vírgula 6.10 à potência de menos 19 fim do exponencial. espaço parêntese esquerdo menos 180 parêntese direito tau igual a 2 vírgula 88.10 à potência de menos 17 fim do exponencial J$

7) UECE - 2014

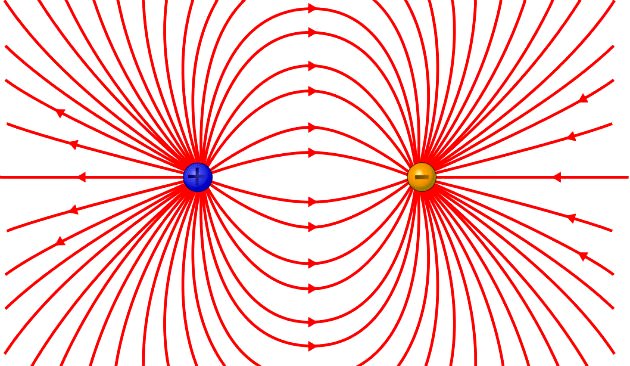
Considere o campo elétrico gerado por duas cargas elétricas puntiformes, de valores iguais e sinais contrários, separadas por uma distância d. Sobre esse vetor campo elétrico nos pontos equidistantes das cargas, é correto afirmar que

a) tem a direção perpendicular à linha que une as duas cargas e o mesmo sentido em todos esses pontos.
b) tem a mesma direção da linha que une as duas cargas, mas varia de sentido para cada ponto analisado.
c) tem a direção perpendicular à linha que une as duas cargas, mas varia de sentido para cada ponto analisado.
d) tem a mesma direção da linha que une as duas cargas e o mesmo sentido em todos esses pontos.

Ver Resposta

Na imagem abaixo estão representadas as linhas de força quando temos duas cargas elétricas de sinais contrários.

Como o vetor campo elétrico tangencia as linhas de força em cada ponto, verificamos que nos pontos equidistantes das cargas o vetor terá a mesma direção da linha que une as duas cargas e o mesmo sentido.

Alternativa: d) tem a mesma direção da linha que une as duas cargas e o mesmo sentido em todos esses pontos.

Para mais exercícios, veja também:

Veja também exercícios de Física (resolvidos) para 3º ano do ensino.

Rosimar Gouveia

Bacharel em Meteorologia pela Universidade Federal do Rio de Janeiro (UFRJ) em 1992, Licenciada em Matemática pela Universidade Federal Fluminense (UFF) em 2006 e Pós-Graduada em Ensino de Física pela Universidade Cruzeiro do Sul em 2011.

Que tal um up?

Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo

Exercícios exclusivos Acesso a centenas de questões com gabaritos

Estude sem publicidade Navegação limpa e focada para evitar distrações