Exercícios sobre Lei de Coulomb (Força elétrica)
A lei de Coulomb é utilizada para calcular o módulo da força elétrica entre duas cargas.
Essa lei diz que a intensidade força é igual ao produto de uma constante, chamada constante eletrostática, pelo módulo do valor das cargas, dividido pelo quadrado da distância entre as cargas, ou seja:
Aproveite a resolução das questões abaixo para tirar suas dúvidas com relação a esse conteúdo de eletrostática.
Questão 1
(Fuvest - 2019) Três pequenas esferas carregadas com carga positiva ocupam os vértices de um triângulo, como mostra a figura. Na parte interna do triângulo, está afixada outra pequena esfera, com carga negativa q. As distâncias dessa carga às outras três podem ser obtidas a partir da figura.
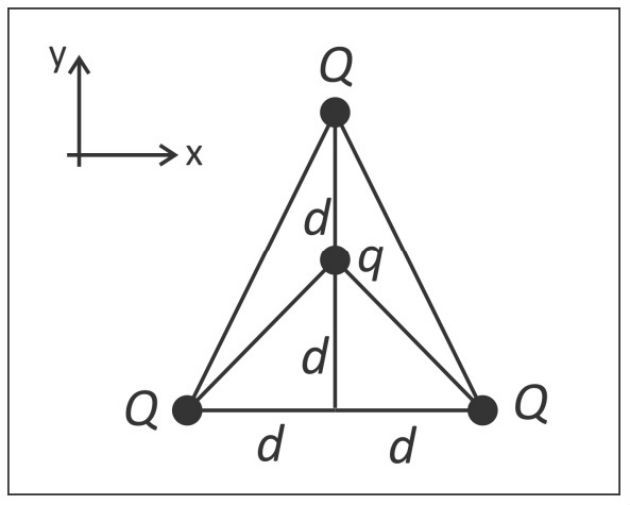
Sendo Q = 2 x 10-4 C, q = - 2 x 10-5 C e ݀d = 6 m, a força elétrica resultante sobre a carga q
(A constante k0 da lei de Coulomb vale 9 x 109 N. m2 /C2)
a) é nula.
b) tem direção do eixo y, sentido para baixo e módulo 1,8 N.
c) tem direção do eixo y, sentido para cima e módulo 1,0 N.
d) tem direção do eixo y, sentido para baixo e módulo 1,0 N.
e) tem direção do eixo y, sentido para cima e módulo 0,3 N.
Para calcular a força resultante na carga q é necessário identificar todas as forças que atuam sobre esta carga. Na imagem abaixo representamos essas forças:
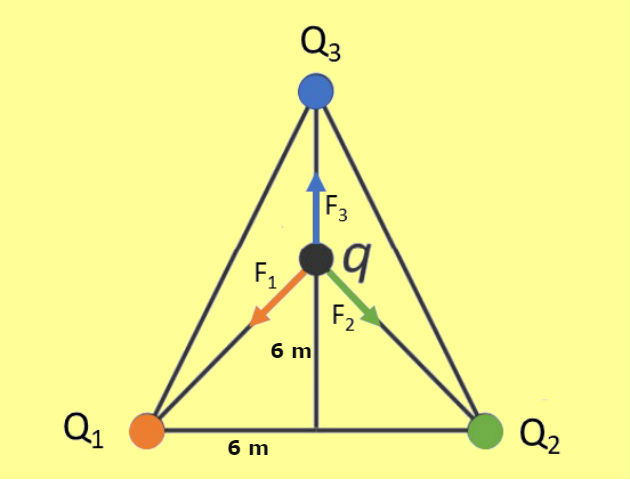
As cargas q e Q1 estão localizadas no vértice do triângulo retângulo indicado na figura e que possui catetos que medem 6 m.
Desta forma, a distância entre essas cargas pode ser encontrada através do teorema de Pitágoras. Assim, temos:
Agora que conhecemos as distâncias entre as cargas q e Q1, podemos calcular a intensidade da força F1 entre elas aplicando a lei de Coulomb:
A intensidade da força F2 entre as cargas q e Q2 também será igual a , pois a distância e o valor das cargas é o mesmo.
Para calcular a força resultante F12 usamos a regra do paralelogramo, conforme imagem abaixo:
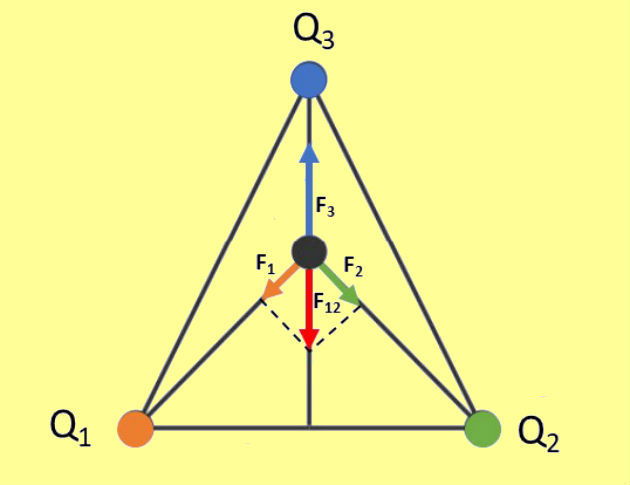
Para calcular o valor da força entre as cargas q e Q3 aplicamos novamente a lei de Coulomb, sendo que a distância entre elas é igual a 6 m. Assim:
Finalmente, iremos calcular a força resultante sobre a carga q. Note que as forças F12 e F3 possuem mesma direção e sentido contrário, logo, a força resultante será igual a subtração dessas forças:
Como F3 possui módulo maior que F12 , a resultante apontará para cima na direção do eixo y.
Alternativa: e) tem direção do eixo y, sentido para cima e módulo 0,3 N.
Exercício 2
(UFRGS - 2017) Seis cargas elétricas iguais a Q estão dispostas, formando um hexágono regular de aresta R, conforme mostra a figura abaixo.
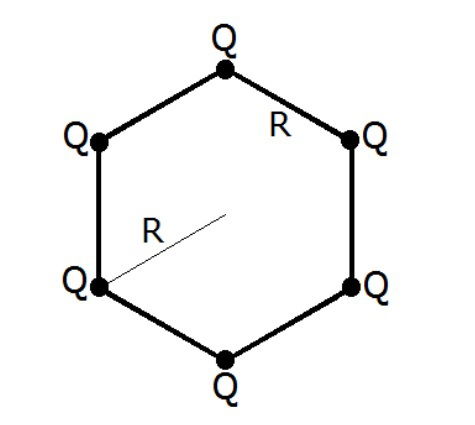
Com base nesse arranjo, sendo k a constante eletrostática, considere as seguintes afirmações.
I - O campo elétrico resultante no centro do hexágono tem módulo igual a
II - O trabalho necessário para se trazer uma carga q, desde o infinito até o centro do hexágono, é igual a
III - A força resultante sobre uma carga de prova q, colocada no centro do hexágono, é nula.
Quais afirmações estão corretas?
a) Apenas I.
b) Apenas II.
c) Apenas I e III.
d) Apenas II e III.
e) I, II e III.
I - O vetor campo elétrico no centro do hexágono é nulo, pois como os vetores de cada carga possuem mesmo módulo eles se anulam mutuamente, conforme figura abaixo:
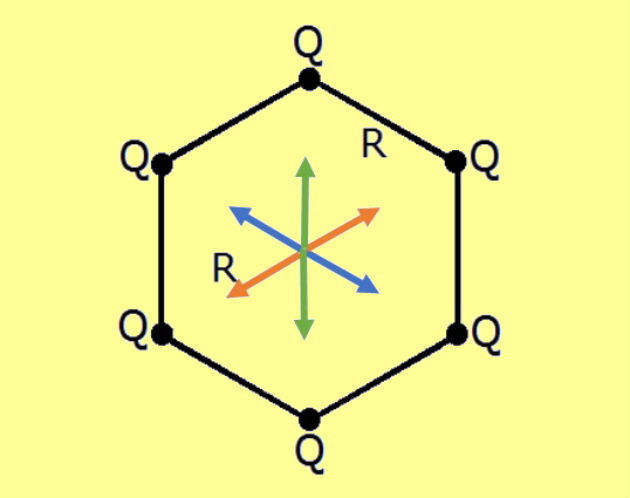
Assim, a primeira afirmativa é falsa.
II - Para calcular o trabalho usamos a seguinte expressão T = q . ΔU, sendo ΔU igual ao potencial no centro do hexágono menos o potencial no infinito.
Vamos definir o potencial no infinito como nulo e o valor do potencial no centro do hexágono será dado pela soma do potencial relativo a cada carga, pois o potencial é uma grandeza escalar.
Como são 6 cargas, então o potencial no centro do hexágono será igual a: . Desta forma, o trabalho será dado por:
, portanto, a segunda afirmação é verdadeira.
III - Para calcular a força resultante no centro do hexágono, fazemos uma soma vetorial. O valor da força resultante no centro do hexágono será igual a zero. Logo, a alternativa também é verdadeira.
Alternativa: d) Apenas II e III.
Questão 3
(PUC/RJ - 2018) Duas cargas elétricas +Q e +4Q estão fixas sobre o eixo x, respectivamente nas posições x = 0,0 m e x = 1,0 m. Uma terceira carga é posicionada entre as duas, sobre o eixo x, tal que se encontra em equilíbrio eletrostático. Qual é a posição da terceira carga, em m?
a) 0,25
b) 0,33
c) 0,40
d) 0,50
e) 0,66
Ao posicionar uma terceira carga entre as duas cargas fixas, independente do seu sinal, teremos duas forças de mesma direção e sentidos contrários atuando nesta carga, conforme figura abaixo:
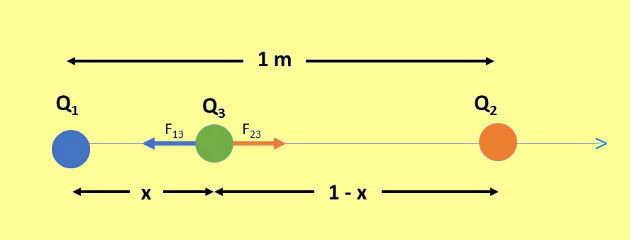
Na figura, consideramos que a carga Q3 é negativa e como a carga está em equilíbrio eletrostático, então a força resultante é igual a zero, assim:
Alternativa: b) 0,33
Questão 4
(PUC/RJ - 2018) Uma carga q0 é colocada em uma posição fixa. Ao colocar uma carga q1 =2q0 a uma distância d de q0 , q1 sofre uma força repulsiva de módulo F. Substituindo q1 por uma carga q2 na mesma posição, q2 sofre uma força atrativa de módulo 2F. Se as cargas q1 e q2 são colocadas a uma distância 2d entre si, a força entre elas é:
a) repulsiva, de módulo F
b) repulsiva, de módulo 2F
c) atrativa, de módulo F
d) atrativa, de módulo 2F
e) atrativa, de módulo 4F
Como a força entre as cargas qo e q1 é de repulsão e entre as cargas qo e q2 é de atração, concluímos que as cargas q1 e q2 possuem sinais opostos. Desta forma, a força entre essas duas cargas será de atração.
Para encontrar o módulo desta força, iremos começar aplicando a lei de Coulomb na primeira situação, ou seja:
Sendo a carga q1 = 2q0 a expressão anterior ficará:
Ao substituir q1 por q2 a força passará a ser igual a:
Vamos isolar a carga q2 em um dois lados da igualdade e substituir o valor de F, assim temos:
Para encontrar a força resultante entre as cargas q1 e q2,vamos novamente aplicar a lei de Coulomb:
Substituindo q1 por 2q0, q2 por 4q0 e d12 por 2d, a expressão anterior ficará:
Observando essa expressão, notamos que o módulo de F12 = F.
Alternativa: c) atrativa, de módulo F
Exercício 5
(PUC/SP - 2019) Uma partícula esférica eletrizada com carga de módulo igual a q, de massa m, quando colocada em uma superfície plana, horizontal, perfeitamente lisa e com seu centro a uma distância d do centro de outra partícula eletrizada, fixa e também com carga de módulo igual a q, é atraída por ação da força elétrica, adquirindo uma aceleração α. Sabe-se que a constante eletrostática do meio vale K e o módulo da aceleração da gravidade vale g.
Determine a nova distância d’, entre os centros das partículas, nessa mesma superfície, porém, com ela agora inclinada de um ângulo θ, em relação ao plano horizontal, para que o sistema de cargas permaneça em equilíbrio estático:
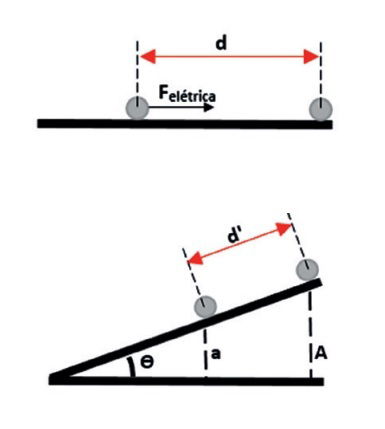
a)
b)
c)
d)
Para que a carga permaneça em equilíbrio no plano inclinado é necessário que a componente da força peso na direção tangente à superfície (Pt) seja equilibrada pela força elétrica.
Na figura abaixo representamos todas as força que agem na carga:
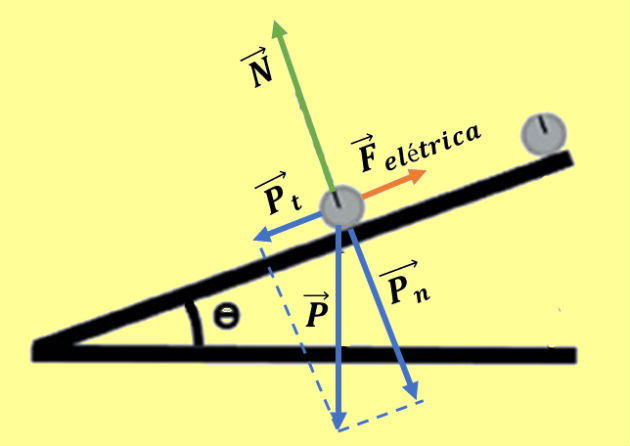
A componente Pt da força peso é dada pela expressão:
Pt = P. sen θ
O seno de um ângulo é igual a divisão da medida do cateto oposto pela medida da hipotenusa, na imagem abaixo identificamos essas medidas:
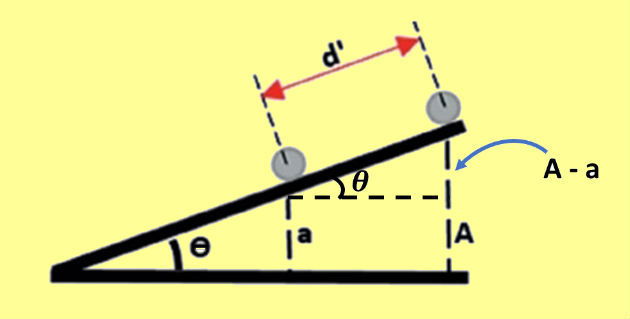
Pela figura, concluímos que o sen θ será dado por:
Substituindo esse valor na expressão da componente do peso, ficamos com:
Como esta força está sendo equilibrada pela força elétrica, temos a seguinte igualdade:
Simplificando a expressão e isolando o d´, temos:
Alternativa:
Exercício 6
(UERJ - 2018) O esquema abaixo representa as esferas metálicas A e B, ambas com massas de 10-3 kg e carga elétrica de módulo igual a 10-6 C. As esferas estão presas por fios isolantes a suportes, e a distância entre elas é de 1 m.
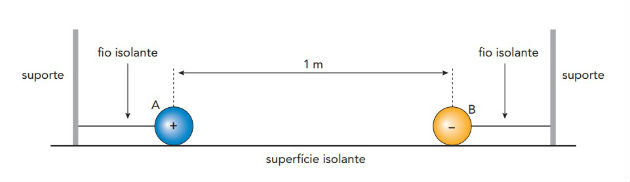
Admita que o fio que prende a esfera A foi cortado e que a força resultante sobre essa esfera corresponde apenas à força de interação elétrica. Calcule a aceleração, em m/s2, adquirida pela esfera A imediatamente após o corte do fio.
Questão 7
(Unicamp - 2014) A atração e a repulsão entre partículas carregadas têm inúmeras aplicações industriais, tal como a pintura eletrostática. As figuras abaixo mostram um mesmo conjunto de partículas carregadas, nos vértices de um quadrado de lado a, que exercem forças eletrostáticas sobre a carga A no centro desse quadrado. Na situação apresentada, o vetor que melhor representa a força resultante agindo sobre a carga A se encontra na figura
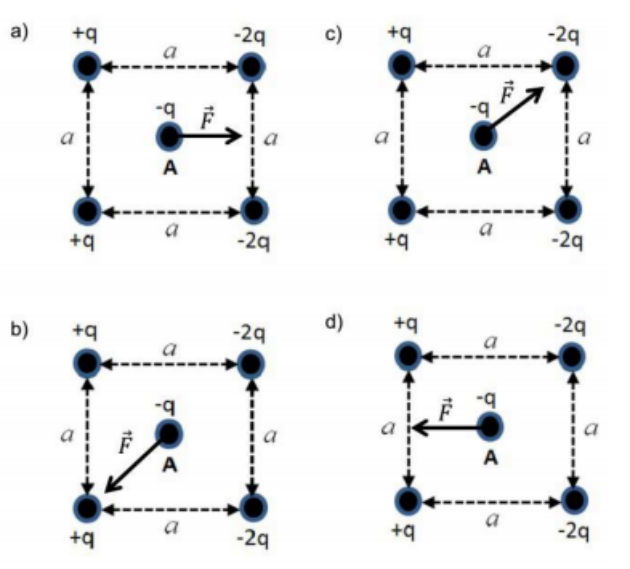
Questão 8
Duas cargas elétricas puntiformes iguais quando distam de 8 cm uma da outra se repelem com uma força de 4,0.10-8 N. Qual será a força entre elas se a distância for duplicada? Adote k=9.109 N.m2/C2 .
a) 1,0.10-8 N
b) 4,0.10-8 N
c) 2,5. 10-7N
d) 8,0.10-8 N
Resposta correta: alternativa a) 1,0.10-8 N
Para resolver esse exercício não precisamos determinar os valores das cargas elétricas, basta colocar na fórmula que a distância é duplicada, ou:
Questão 9
Uma carga teste q fica sob a ação de uma força elétrica atrativa F1 igual a 2,0.10-5 N quando dista 0,5 m de uma carga Q1 igual a +10C. Qual é o valor da carga q? Ela é positiva ou negativa? Adote k=9.109 N.m2/C2
a) 5,6.10-15 C, negativa
b) 5,6.10-15 C, positiva
c) 5,6.10-17 C, negativa
d) 5,6.10-17 C, positiva
Resposta correta: alternativa c) 5,6.10-17 C, negativa
A módulo da força elétrica é dada por:
Questão 10
Duas cargas puntiformes exatamente iguais sofrem uma força igual a 3,6.10-4 N quando distam 3 metros uma da outra. Qual é o valor das cargas? Adote k = 9.109 Nm2/C2.
a) 5.10-6 C
b) 6.10-6 C
c) 5.10-7 C
d) 6.10-7 C
Resposta correta: alternativa d) 6.10-7 C
Observe que o enunciado dá o valor da força de 3,6.10-4 N quando as cargas estão à distância de 3 metros.
Substituindo os valores na equação da força elétrica temos:
Questão 11
Uma carga q igual a -10C está a 5 metros de distância de uma carga Q igual a 10C. Qual é a aceleração da carga q, considerando que sua massa é 0,1 Kg? Adote k=9.109 N.m2/C2
a) 1 m/s2
b) 3,6. 1010 m/s2
c) 3,6. 1011 m/s2
d) 0,9 m/s2
Resposta correta: alternativa c) 3,6. 1011 m/s2
A força elétrica nesse caso é igual à força resultante que atua sobre a carga, que pela segunda Lei de Newton é F=m.a
A força elétrica é:
Igualando a força elétrica à força de Newton, vem:
Questão 12
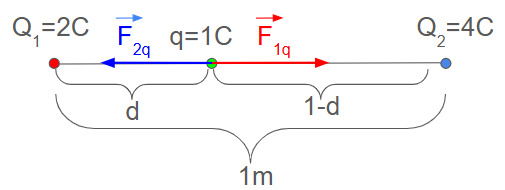
Uma carga teste q igual a 1C é colocada entre duas cargas Q1 e Q2, respectivamente iguais a 2C e 4C que distam 1 metro entre si. Qual é a distância d entre as cargas Q1 e q que faz com que a força resultante sobre a carga teste q seja nula?
a) 1,0 m
b) 0,4 m
c) 0,5 m
d) 1,2 m
e) A força resultante sobre q nunca é nula.
Resposta correta: alternativa b) 0,4 m
A força elétrica entre duas cargas q e Q é dada por:
Observe que todas as cargas são positivas, então ambas as forças são repulsivas. A figura abaixo representa o problema:
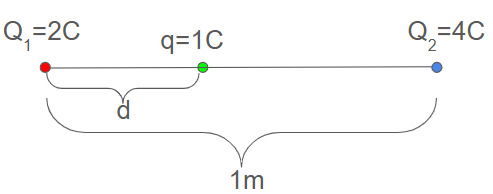
A carga Q1 exerce sobre q uma força repulsiva F1q que aponta para a direita, a carga Q2 exerce sobre q uma força repulsiva F2q que aponta para a esquerda. As forças sobre q são:
Queremos que a força resultante sobe q seja nula, para isso F1q=F2q ou:
Agora usamos Baskara para descobrir as raízes desse polinômio e escolher a que está entre as cargas Q1 e Q2:
O valor da raíz que está entre as carga é a de 0,41m.
Para saber mais, veja Lei de Coulomb.
Para mais exercícios:
- Exercícios de eletrostática (com questões resolvidas e comentadas)
- Exercício sobre carga elétrica (com respostas explicadas)
- Exercícios de campo elétrico (com questões explicadas)
ASTH, Rafael. Exercícios sobre Lei de Coulomb (Força elétrica). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/lei-de-coulomb-exercicios/. Acesso em:




