Exercícios sobre vetor campo elétrico (com gabarito resolvido e explicado)

Com o aumento da utilização de dispositivos eletrônicos e redes de comunicação sem fio, a poluição eletromagnética tem sido um tema amplamente discutido. Entender os efeitos do campo elétrico gerado por essas tecnologias é fundamental para avaliar impactos na saúde e no meio ambiente.

O campo elétrico, representado por um vetor, é definido como a força elétrica que uma carga de prova experimenta por unidade de carga.

Considere duas cargas elétricas Q1=+3 μC e Q2=−2 μC, fixas em uma linha reta e separadas por uma distância de d = 4 m. Um ponto P está localizado a 1 m de Q1 e 3 m de Q2. Calcule o módulo do vetor campo elétrico resultante no ponto P.

Considere .

A eletroforese é uma técnica amplamente utilizada em laboratórios de análises clínicas e pesquisa genética para separar biomoléculas como proteínas e fragmentos de DNA. O princípio baseia-se na aplicação de um campo elétrico uniforme que exerce forças sobre partículas carregadas, permitindo sua separação conforme a carga e tamanho.

Em um laboratório de diagnóstico molecular, duas cargas puntiformes idênticas +Q estão posicionadas simetricamente em relação ao eixo central de um equipamento de eletroforese. As cargas estão separadas por uma distância de 2d e criam um padrão de campo elétrico na região entre elas.

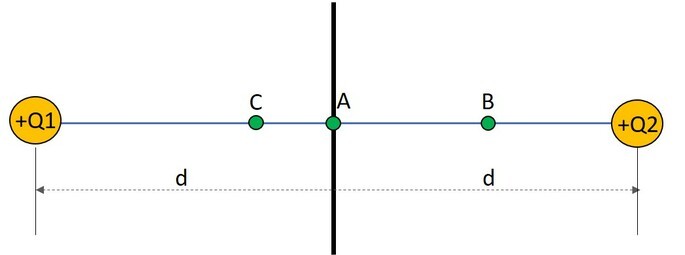
Considerando os pontos:

• Ponto A: localizado no centro geométrico entre as duas cargas;
• Ponto B: localizado à distância d/2 do ponto A, sobre a linha que une as cargas;
• Ponto C: localizado sobre a linha que une as cargas, à distância 3d/4 da carga 1.

Qual das afirmações sobre a intensidade do campo elétrico resultante nesses pontos está CORRETA?

A proteção contra descargas atmosféricas em aeronaves é um desafio crítico para a aviação comercial brasileira. O Brasil possui um dos maiores números de raios por ano no mundo, tornando essencial o entendimento dos fenômenos eletrostáticos para garantir a segurança dos voos. Durante tempestades, as aeronaves podem acumular cargas elétricas significativas devido ao atrito com partículas de gelo e vapor dʼágua nas nuvens.

Os engenheiros aeronáuticos utilizam conceitos de campo elétrico para projetar sistemas de proteção, incluindo para-raios especiais nas extremidades das asas e fuselagem. O entendimento das propriedades do campo elétrico é fundamental para evitar interferências nos sistemas eletrônicos de navegação e comunicação durante voos em condições adversas.

Considerando os princípios físicos que regem o comportamento do campo elétrico em situações como a descrita, analise as afirmativas abaixo e classifique-as como VERDADEIRAS (V) ou FALSAS (F):

I. O vetor campo elétrico em um ponto qualquer do espaço independe da presença de cargas de prova nesse ponto, sendo uma propriedade exclusiva da distribuição de cargas que o gera.

II. Em uma região onde existe um campo elétrico uniforme, todas as linhas de força são paralelas entre si e possuem a mesma intensidade.

III. O campo elétrico no interior de um condutor em equilíbrio eletrostático é sempre nulo, independentemente da forma geométrica do condutor.

IV. Quando uma carga elétrica positiva é colocada em uma região de campo elétrico, a força elétrica sobre ela tem sempre o mesmo sentido do vetor campo elétrico naquela região.

V. O campo elétrico resultante produzido por duas cargas puntiformes de mesmo sinal é sempre diferente de zero em qualquer ponto do espaço.

Assinale a alternativa que apresenta a classificação CORRETA das afirmativas:

O tratamento de câncer por radioterapia utiliza feixes de partículas carregadas que são aceleradas e direcionadas com precisão para destruir células tumorais. No Hospital do Câncer de Barretos, um dos principais centros de referência oncológica do Brasil, equipamentos de radioterapia empregam campos elétricos intensos para controlar o movimento de partículas ionizadas durante o tratamento.

Em um acelerador linear utilizado para radioterapia, uma carga geradora positiva Q = +2,0 × 10⁻⁸ C está fixa em uma determinada posição. A uma distância de 0,30 m dessa carga, os técnicos posicionam uma carga de prova negativa q = -4,0 × 10⁻¹⁰ C para estudar o comportamento do sistema antes de calibrar o equipamento.

Considerando a constante eletrostática k = 9,0 × 10⁹ N·m²/C², analise as características do vetor campo elétrico e da força elétrica nessa configuração:

I. O vetor campo elétrico criado pela carga geradora Q aponta radialmente para fora, afastando-se da carga positiva.

II. A força elétrica sobre a carga de prova q tem sentido oposto ao vetor campo elétrico no ponto onde ela se encontra.

III. O vetor campo elétrico independe da presença da carga de prova negativa, sendo determinado somente pela carga geradora Q.

IV. A carga de prova q será atraída em direção à carga geradora Q devido à força eletrostática.

Estão CORRETAS as afirmativas:

O monitoramento de poluentes atmosféricos é essencial para a qualidade do ar nas grandes cidades brasileiras. O Instituto Nacional de Pesquisas Espaciais (INPE) utiliza sensores eletrostáticos para detectar partículas carregadas presentes na atmosfera, como poeira, fuligem e aerossóis industriais. Esses sensores funcionam baseados no princípio de que partículas eletricamente carregadas geram campos elétricos detectáveis.

Em um experimento de calibração realizado em São Paulo, duas partículas poluentes eletricamente carregadas, Q₁ e Q₂, são posicionadas em pontos específicos de uma grade de coordenadas. A partícula Q₁ está localizada na posição (2, 1) e a partícula Q₂ na posição (6, 1). Os vetores mostram o campo elétrico gerado por Q₁ no ponto A (posição 2, 4) e o campo elétrico gerado por Q₂ no ponto B (posição 6, 4).

Considerando o princípio da superposição, quando as partículas Q₁ e Q₂ são deslocadas simultaneamente para as posições A e B respectivamente, o campo elétrico resultante no ponto C (posição 4, 4) será representado pelo vetor:

Os sensores elétricos utilizados em equipamentos médicos, como os eletrocardiógrafos, são projetados para medir os efeitos de campos elétricos gerados no corpo humano. O entendimento desses campos é crucial para calibrar e melhorar a precisão dos aparelhos.

Considere duas cargas pontuais Q1=+5 μC e Q2=−5 μC, separadas por uma distância d =2 m. O ponto P está exatamente no meio do segmento que une essas duas cargas. Qual é o módulo do vetor campo elétrico resultante no ponto P?

Considere:

O campo elétrico é uma grandeza vetorial que caracteriza a interação elétrica entre cargas. Quando uma carga de prova q é colocada em uma região onde existe um campo elétrico gerado por outra carga, uma força elétrica atua sobre ela, dependendo da natureza das cargas envolvidas.

Considere uma carga geradora Q＞0 fixa no espaço e uma carga de prova q＜0. Analise as afirmações a seguir e determine se são verdadeiras (V) ou falsas (F):

1. A força elétrica sobre a carga de prova q tem a mesma direção e o mesmo sentido do vetor campo elétrico gerado por Q.
2. A força elétrica sobre q tem a mesma direção do vetor campo elétrico, mas sentido oposto.
3. O vetor campo elétrico gerado por Q aponta radialmente para fora de Q, independentemente da carga de prova.
4. O vetor campo elétrico gerado por Q aponta radialmente para dentro de Q, devido à presença de q.
5. O sentido do vetor campo elétrico depende somente da carga geradora Q e não da carga de prova q.