Perímetro do Círculo

O perímetro de um círculo é a medida do comprimento da linha que o contorna, isto é, o perímetro do círculo é o comprimento da circunferência. É como desenrolar a circunferência, esticar essa linha e medir o seu comprimento.

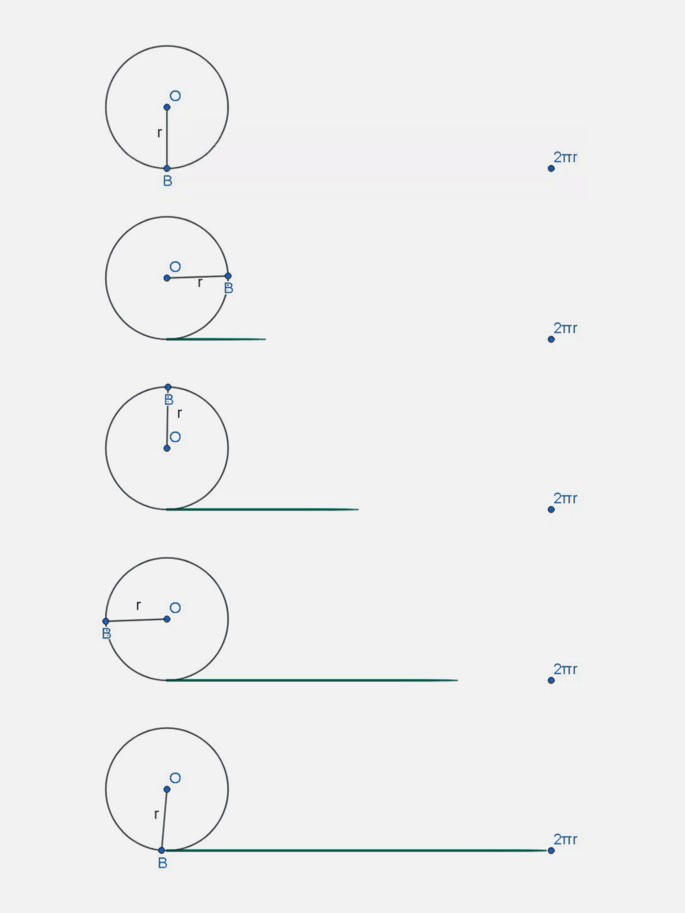
Lembre-se se que o perímetro é a soma de todos os lados da figura. Por exemplo, se vamos encontrar o perímetro do triângulo, devemos somar o valor das medidas dos três lados da figura.

Mas, no caso do círculo, ele não é um polígono e, portanto, não possui lados, dessa forma recorremos ao conceito de cálculo para mostrar que o comprimento de uma circunferência é exatamente o perímetro do círculo.

Fórmula do perímetro ou comprimento da circunferência

Vale lembrar que o círculo é uma figura que não apresenta segmentos de retas. Portanto, o perímetro do círculo equivale ao comprimento da circunferência. É importante destacar seus elementos principais.

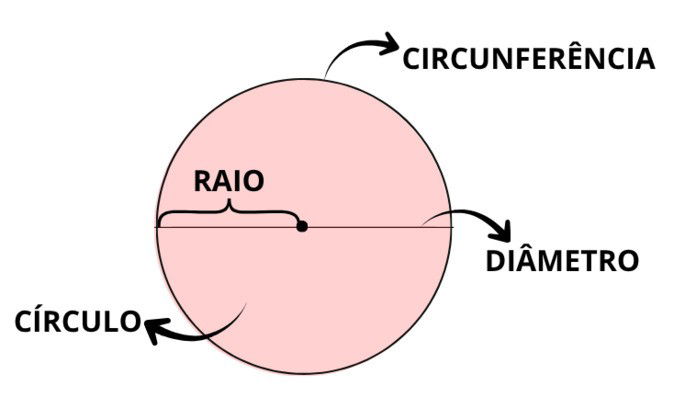
Sabemos da geometria plana que a área de um polígono convexo regular de lados e apótema é dada por:

Onde,

é o semiperímetro
é o apótema

Como queremos encontrar o comprimento (perímetro) do círculo podemos, sem perda de generalidade, supor que:

A quantidade de lados tende a infinito, o apótema tende para o raio e o semiperímetro tende para metade do comprimento da circunferência .

Igualando as áreas do círculo e do polígono quando e cancelando um fator teremos:

Fique atento!

O valor do raio é o principal elemento que devemos ter para encontrar o perímetro do círculo. O valor de pode aparecer como uma aproximação na questão como por exemplo: ou , pois trata-se de uma constante matemática, ou seja, um número irracional. Ou ainda pode vir apenas como seu valor exato indicado que é .

Essa constante foi mostrada por Arquimedes no século III a.C. com uma incrível aproximação de .

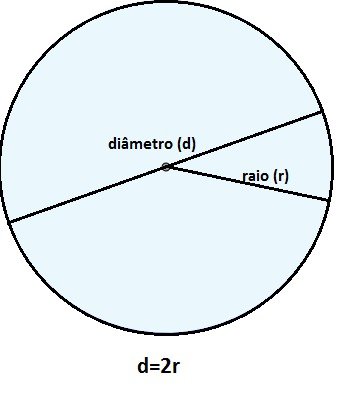
Feita essa observação, lembre-se que o raio é a medida do centro da figura até sua extremidade. Assim, o raio mede a metade do diâmetro.

Passo a passo para calcular o perímetro do círculo (exemplos)

Exemplo 1

Um círculo possui perímetro de 62,8 m. Calcule o valor do raio e use .

O perímetro do círculo ou comprimento da circunferência é dado por:

Exemplo 2

Duas rodas, a menor de raio 7 cm e a maior de raio R são unidas por uma correia. Enquanto a maior dá uma volta completa, a menor dá 8 voltas. Sendo assim, determine o raio da circunferência maior.

De acordo com as informações do enunciado, podemos ver que enquanto a roda maior dá uma volta completa, a menor dá 8 voltas completas, ou seja, o perímetro da roda maior é igual a 8 vezes o da roda menor.

Exemplo 3

Uma pista de atletismo tem formato circular com raio de 50 m. O treinador quer saber quantos metros um atleta percorre ao dar 7 voltas completas na pista. (Use ).

Queremos saber inicialmente a distância percorrida em um volta, ou seja, o perímetro do círculo.

Como são 7 voltas, basta multiplicarmos o perímetro por 7.

Diferença entre círculo e circunferência

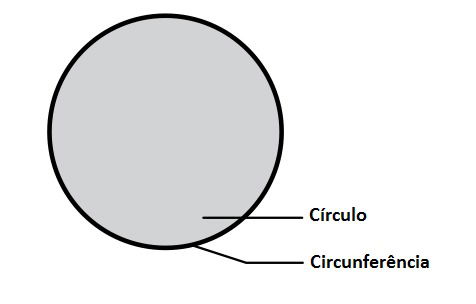
Como vimos anteriormente, embora muitas pessoas utilizem o termo círculo e circunferência como sinônimos, não apenas em matemática, mas semanticamente eles representam dois conceitos distintos.

• Círculo: é a parte interna da circunferência, ou seja, é a figura plana delimitada por ela.
• Circunferência: é o contorno (linha curva) que limita o círculo, ou ainda, o lugar geométrico dos pontos do plano equidistantes de um ponto dado que é o centro.

Exercícios resolvidos

1. Calcule o perímetro de um círculo com diâmetro de 6 cm.

2. Determine o valor do diâmetro de um canteiro que apresenta perímetro de 20 m.

3. João percorre todos os dias 6 quilômetros em torno de um lago circular. No total, ele dá 12 voltas no local. Qual o valor do perímetro desse círculo em metros?

4. Uma bicicleta possui roda de aro 29 (raio de 35 cm). Quantas voltas completas a roda deverá dar para percorrer 5 km? (Use )

5. Uma roda gigante de parque de diversões tem raio de 15 m. Ao completar 12 voltas completas durante um passeio, quantos metros uma pessoa percorreu? (Use )

Veja também:

Área do círculo

Áreas de figuras planas

Geometria plana