Vértice da Parábola

O vértice da parábola corresponde ao ponto em que o gráfico de uma função do 2º grau muda de sentido. A função do segundo grau, também chamada de quadrática, é a função do tipo f(x) = ax² + bx + c.

Usando um plano cartesiano, podemos traçar o gráfico de uma função quadrática considerando os pontos de coordenadas (x,y) que pertencem a função.

Na imagem abaixo, temos o gráfico da função f(x) = x² - 2x - 1 e o ponto que representa seu vértice.

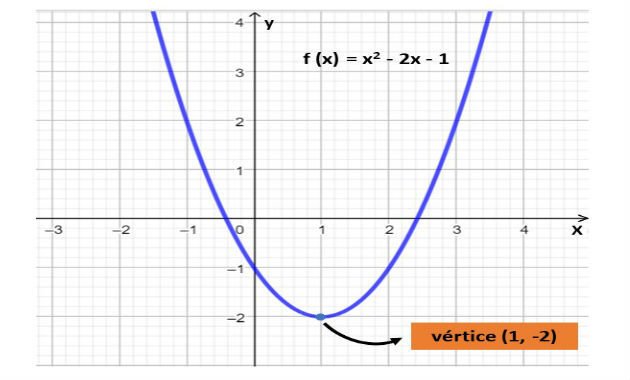
Coordenadas do Vértice

As coordenadas do vértice de uma função quadrática, dada por f(x) = ax² + bx +c, podem ser encontradas através das seguintes fórmulas:

Sendo Δ = b² - 4.a.c

Exemplo

Encontre as coordenadas do vértice da função f(x) = - x² + 4x - 2.

Solução

Para encontrar as coordenadas do vértice, aplicaremos as fórmulas acima. Para isso, vamos calcular o valor do Δ, considerando a = - 1, b = 4 e c = - 2. Assim temos:

Δ = 4² - 4 . (- 1). (- 2) = 16 - 8 = 8

Substituindo os valores, encontramos:

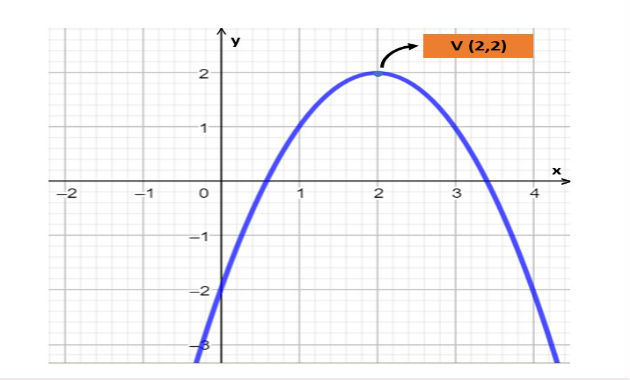
Portanto, o ponto do vértice tem coordenadas V (2, 2), conforme indicado na imagem abaixo:

Valor máximo e mínimo

De acordo com o sinal do coeficiente a da função do segundo grau, a parábola poderá apresentar sua concavidade voltada para cima ou para baixo.

Quando o coeficiente a for negativo, a concavidade da parábola estará para baixo. Neste caso, o vértice será o máximo valor atingido pela função.

Para funções com coeficiente a positivo, a concavidade estará voltada para cima e o vértice representará o mínimo valor da função.

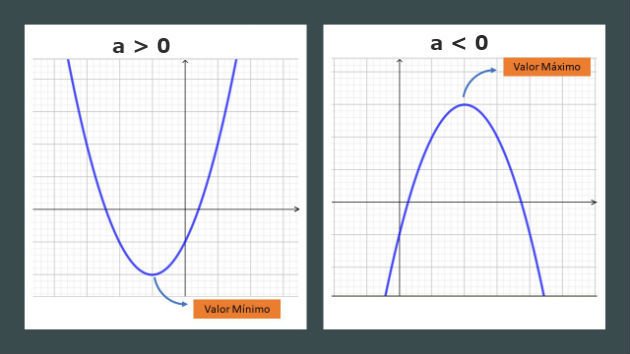
Imagem da função

Como o vértice representa o ponto máximo ou mínimo da função do 2º grau, ele é usado para definir o conjunto imagem desta função, ou seja, os valores de y que pertencem a função.

Desta forma, existem duas possibilidades para o conjunto imagem da função quadrática:

• Para a > 0 o conjunto imagem será:
• Para a < 0 o conjunto imagem será:

Por exemplo, para definir a imagem da função f(x) = x² + 2 x - 3, devemos encontrar o valor do y do vértice da função. Aplicando a fórmula, descobrimos que o valor do y_v é - 4.

Como o coeficiente a da função é positivo (a > 0), a parábola tem concavidade para cima, Então, este ponto será o valor mínimo da função, conforme indicado na imagem abaixo:

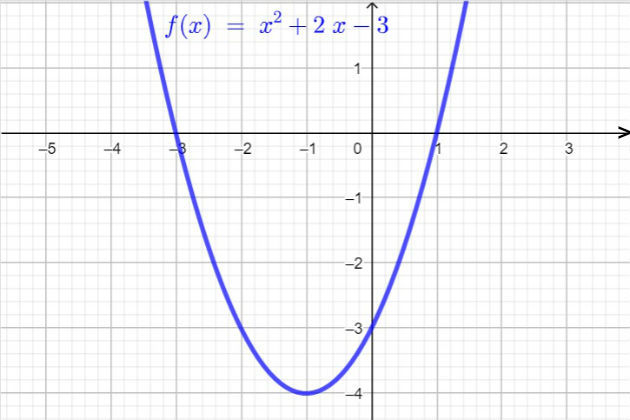
Portanto, todos os valores assumidos pela função serão maiores que - 4. Assim, f(x) = x² + 2x - 3 terá conjunto imagem dado por:

Questões Resolvidas

1) Enem - 2015

Um estudante está pesquisando o desenvolvimento de certo tipo de bactéria. Para essa pesquisa, ele utiliza uma estufa para armazenar as bactérias. A temperatura no interior dessa estufa, em graus Celsius, é dada pela expressão T(h) = - h² + 22 h - 85, em que h representa as horas do dia. Sabe-se que o número de bactérias é o maior possível quando a estufa atinge sua temperatura máxima e, nesse momento, ele deve retirá-las da estufa. A tabela associa intervalos de temperatura, em graus Celsius, com as classificações: muito baixa, baixa, média, alta e muito alta.

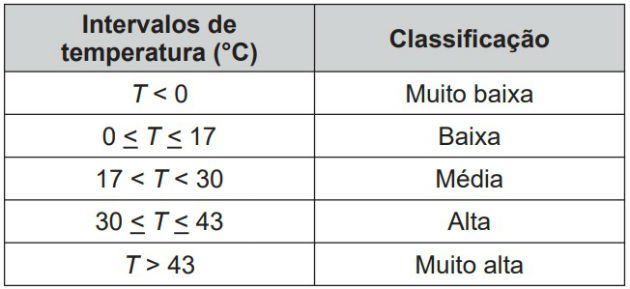
Quando o estudante obtém o maior número possível de bactérias, a temperatura no interior da estufa está classificada como

a) muito baixa.
b) baixa.
c) média.
d) alta.
e) muito alta.

2) UERJ - 2016

Observe a função f, definida por: f (x) = x² - 2kx + 29, para x ∈ IR. Se f (x) ≥ 4, para todo número real x, o valor mínimo da função f é 4.

Assim, o valor positivo do parâmetro k é:

a) 5
b) 6
c) 10
d) 15

Para mais exercícios:

Exercícios de função quadrática (questões resolvidas e comentadas)

Exercícios sobre as coordenadas do vértice da parábola (com gabarito)

Veja também: Equação do Segundo Grau